往期文章：

• 【计算复杂性理论】证明复杂性（Proof Complexity）（一）：简介
  
• 【计算复杂性理论】证明复杂性（二）：归结（Resolution）与扩展归结（Extended Resolution）证明系统
• 【计算复杂性理论】证明复杂性（三）：弗雷格（Frege）与扩展弗雷格（Extended Frege）证明系统
• 【计算复杂性理论】证明复杂性（四）：相继式演算（Sequent Calculus）
• 【计算复杂性理论】证明复杂性（五）：量化命题演算（Quantified Propositional Calculus）
  
• 【计算复杂性理论】证明复杂性（六）：其他证明系统简介
  
• 【计算复杂性理论】证明复杂性（七）：有界算术（Bounded Arithmetic）与IΔ₀理论

1985年，Haken的论文^[1]证明了归结证明系统在命题鸽巢原理上有指数级下界，即命题鸽巢原理不存在多项式大小的归结证明。这项发现说明了归结的强度非常弱，而且因为DPLL、CDCL算法对应的证明系统不强于归结，这也说明了DPLL、CDCL算法的时间复杂度是指数级别的。

关于文字、子句、合取范式等术语的定义请见【算法/图论】2-SAT问题详解。

我们规定：对于变量$v$，子句$C$如果包含文字$v$，则称$v$在$C$中是以肯定的形式出现的；若包含文字$\neg v$，则称$v$在$C$中是以否定的形式出现的。

一、命题鸽巢原理

鸽巢原理（pigeonhole principle）是说，如果$n$个鸽子要飞到$m$个巢里面，$n>m$，且每个巢最多只能有一个鸽子，那么这一定是不可能的。在国内对应的叫法是抽屉原理。

命题鸽巢原理（propositional pigeonhole principle）就是鸽巢原理表示成命题公式的形式。这篇文章只讨论$m=n-1$，即巢比鸽子少一个的情况。定义变量$P_{ik}(1\le i\le n,1\le k\le n-1)$表示编号为$i$的鸽子飞进编号为$k$的巢里。定义命题公式${\mathrm{PHP}}_n^{n-1}$为下列公式的合取：

1. $P_{i1}\vee P_{i2}\vee \cdots \vee P_{i,n-1}$，$1\le i\le n$
2. $\neg P_{ik}\vee \neg P_{jk}$，$1\le i<j\le n$，$1\le k\le n-1$

${\mathrm{PHP}}_n^{n-1}$表示的就是$n$个鸽子可以飞到$m$个巢里面并且每个巢里只有不超过一个鸽子。第一条表示每个鸽子必须飞到至少一个巢里面；第二条表示任两个鸽子不能飞到同一个巢里面，这样就保证了每个巢里的鸽子数量小于$2$。我们不必限制每个鸽子只能飞到一个巢里面，因为如果一个鸽子飞到超过一个巢里面了，其他鸽子的空间就更小了。显然，${\mathrm{PHP}}_n^{n-1}$是不可满足的（即$\neg {\mathrm{PHP}}_n^{n-1}$是永真式），而我们要讨论的就是用归结证明系统反驳${\mathrm{PHP}}_n^{n-1}$的复杂性。

二、定理的表述和证明的大体思路

定理（Haken 1985^[1]） 存在一个常数$c>1$，使得对于充分大的$n$，${\mathrm{PHP}}_n^{n-1}$的任何归结反驳都包含至少$c^n$个不同的子句。

证明思路：对于某个固定的$n$，假设我们有${\mathrm{PHP}}_n^{n-1}$的一个归结反驳$R$。在接下来的证明中，我们令$k=\lfloor \frac{n-1}{4}\rfloor$。

我们可以把变量表示成表格的形式。每行对应同一只鸽子，每列对应同一个巢。比如${\mathrm{PHP}}_3^2$的变量表格如下：

鸽子\巢	$1$	$2$
$1$	$P_{11}$	$P_{12}$
$2$	$P_{21}$	$P_{22}$
$3$	$P_{31}$	$P_{32}$

定义$\mathrm{FS}1$是满足所有下列条件的集合：它包含${\mathrm{PHP}}_n^{n-1}$的$k$个变量，且没有两个变量在表格中处于同一行或同一列。令$h(n)$是$\mathrm{FS}1$中的元素个数。对于$\mathrm{FS}1$中的每个变量集合$S$，我们在$R$中找到一个对应的“高复杂度子句”（highly complex clause, HCC）。我们定义一个函数$g(n)$并证明任何一个高复杂度子句至多对应$\mathrm{FS}1$中的$g(n)$个元素。因此，$R$中至少包含$f(n)=\frac{h(n)}{g(n)}$个不同的子句。我们将会证明$f(n)$是指数函数。∎

接下来，我们填补这个证明的详细内容。

二、关键赋值CTA

我们按如下方式定义关键赋值（critical truth assignment, CTA）：考虑为变量表格的每一格赋$0$和$1$，如果除了某一行变量的赋值全为$0$（称这一行为零行）外，其余格子的赋值满足：每一行恰有一个$1$、每一列也恰有一个$1$，那么称这个赋值为关键赋值。比如下面这个例子，鸽子的数量为$4$，第三行为零行：

鸽子\巢	$1$	$2$	$3$
$1$	$1$	$0$	$0$
$2$	$0$	$0$	$1$
$3$	$0$	$0$	$0$
$4$	$0$	$1$	$0$

实际上就是给除了第三只鸽子外的其他鸽子安排了合适的巢。关键赋值的含义就是舍弃其中一个鸽子，给其他鸽子分别找到一一对应的巢。关键赋值有$n!$个（舍弃一只鸽子有$n$种方案，其他鸽子与巢一一对应有$(n-1)!$种方案）。令$\mathcal{C}\mathcal{T}\mathcal{A}$为所有关键赋值的集合，每个关键赋值会使${\mathrm{PHP}}_n^{n-1}$中的一个子句为假，那就是规定了零行对应的鸽子至少应该飞进一个巢的子句。上面这个例子中为假的子句就是$P_{31}\vee P_{32}\vee P_{33}$。

如果一个关键赋值$V$中第$r$行$c$列为$1$，则称行$r$和列$c$关于$V$相对应。零行不与任何列相对应。上面的例子中，行$1$、$2$、$3$分别与列$1$、$3$、$2$对应。

三、半零子句HZC

定义归结反驳$R$中的半零子句（half zero clause, HZC）为任何满足下列条件的子句$C$：存在某一行（称为关键行），使得$C$包含这一行的恰好$2k$个变量，这$2k$个变量以肯定的形式出现在$C$中。比如当$n=5$时，$k=1$，那么$P_{22}\vee \neg P_{43}\vee P_{51}\vee P_{53}$就是一个半零子句，第$5$行是关键行。对于一个关键赋值$V$和半零子句$C$，如果$C$的关键行就是$V$的零行，而且$C$在赋值$V$下的取值为假，那么我们就称$C$代表（present）$V$。我们令所有半零子句构成的集合为$\mathcal{H}\mathcal{ZC}$。

引理1 若$C$代表$V$，则$C$在变量表格的每行和每列中至多有一个以否定的形式出现的变量；特别地，$C$的关键行没有以否定的形式出现的变量。

证明：只用证前半句话。由于$C$是一个子句（即简单析取式），要让它为假，必须让其中每个文字的赋值为$0$。显然，$C$中关键行的文字的赋值是为$0$的；因此只需考虑非关键行。如果$P_{ik}$在$V$下的赋值为$0$，那么该变量如果在$C$中出现，要让$C$不可满足，$P_{ik}$只能以肯定的形式出现。只有在$V$下的赋值为$1$的变量才能以否定的形式出现。而$V$中每行、每列至多只有一个变量赋值为$1$，因此$C$在每行、每列至多有一个以否定的形式出现的变量。∎

引理2 每个关键赋值至少被一个半零子句代表。

证明：对于一个关键赋值$V$，我们重点要证明一个归结反驳$R$中必须出现一个能够代表$V$的半零子句。令$q$是$V$的零行对应的鸽子的编号（即编号为$q$个鸽子在赋值$V$下是无家可归的）。这里会用到一个事实：如果子句$C,D$归结的结果是$E$，那么使$E$为假的赋值必使$C$或$D$为假。这是因为，$E$是$C\wedge D$的推论，使$C\wedge D$为真的赋值必然使$E$为真，而$E$为假，所以$C\wedge D$为假，即$C$或$D$为假。因此，如果关键赋值$V$使某个子句$E$为假，而$E$又是$C,D$归结得到的，那么$V$必然使$C,D$中的至少一个为假。由于空子句是$R$的最后一个子句，关键赋值一定使空子句为假，故可以令$E$为空子句。假设我们站在$E$上，而$V$使$C$为假，那我们就跳到$C$处；如果$C$是$F,G$归结而来而$V$使$F$为假，我们就跳到$F$处；一直这样追根溯源，每次我们所到的子句在$V$下的取值都为假，直到跳到${\mathrm{PHP}}_n^{n-1}$的一个子句为止。根据引理1，这个子句必然是$P_{i1}\vee P_{i2}\vee \cdots \vee P_{i,n-1}$的形式（另一种子句一行有两个否定出现的变量，不可能在$V$下赋值为假）。要让这种形式的子句为假，就要求其包含的变量的赋值全为$0$。而$V$只有第$q$行赋值全为$0$，所以这个子句一定是$P_{q1}\vee P_{q2}\vee \cdots \vee P_{q,n-1}$。现在考虑从$P_{q1}\vee P_{q2}\vee \cdots \vee P_{q,n-1}$到$E$的归结路径。每次归结，子句中有一个变量被消除，同时可能有其他文字被加进来。对于第$q$行，每次至多有一个变量被消除，同时可能有其他出现形式为肯定的变量加进来。第$q$行永远不会出现形式为否定的变量，因为$V$对第$q$行所有变量的赋值为$0$。$E$是空子句，不含任何变量，所以在归结路径上子句中第$q$行的变量个数从$n-1$开始到$0$结束，中间有增有减，不过减的时候最多减$1$。因此，总有一时刻使得第$q$行的变量个数恰为$2k$，这个子句就代表$V$的半零子句。∎

如果一个子句$D$经历若干次归结后得到子句$C$，则称$D$是$C$的一个前驱子句。

引理3 设$R$中有子句$C$在关键赋值$V$下的取值为假，且$V$的零行为第$q$行。则要么$C$中至少包含$2k$个以肯定的形式出现的第$q$行的变量，要么$C$的某个前驱子句$D$是半零子句且代表$V$。

证明提要：还是考虑第$q$行的变量个数。如果$C$中包含的第$q$行的变量个数小于$2k$，因为归结的过程中第$q$行的变量个数每次至多减$1$，所以一定有某个前驱子句$D$中第$q$行的变量个数是$2k$。∎

四、相邻的关键赋值

设$V$和$W$是两个关键赋值，并设$q,r$分别是$V$和$W$关键行的编号。如果$W$是$V$交换$q,r$两行的结果，则称$W$和$V$是相邻的。我们说$W$是$V$的$r$-邻居，$V$是$W$的$q$-邻居。

引理4 设半零子句$C$代表关键赋值$V$，其中$V$的零行为第$q$行。设$r$是不同于第$q$行的一行，并设列$s$和行$r$关于$V$对应（即$V$给$P_{rs}$赋值为$1$）。假设$P_{qs}$在$C$中不以肯定的形式出现（可以不出现），$P_{rs}$在$C$中不以否定的形式出现（可以不出现），则$V$的$r$-邻居$W$使$C$的取值为假。

证明：$V$的第$r$行只给一个变量$P_{rs}$赋值为$1$，因此$V$和$W$只有对$P_{qs}$、$P_{rs}$的赋值有区别。考虑变量$P_{qs}$，它在$C$中不以肯定的形式出现，那它要么不出现、要么以否定的形式出现。但是如果它以否定的形式出现，那么由于$V$给$P_{qs}$的赋值为$0$（这是因为$q$是零行），$C$就被满足了，所以$P_{qs}$只能在$C$中不出现。同理，$P_{rs}$要么不出现、要么以肯定的形式出现，但$V$给$P_{qs}$的赋值为$1$，所以只能不出现。因此，$P_{qs}$和$P_{rs}$在$C$中均不出现，而$V$和$W$赋值的差异仅仅在于这两个变量，所以把$V$换成$W$对$C$没有影响，因此$W$使$C$的取值为假。∎

五、高复杂度子句

高复杂度子句（highly complex clause, HCC）组成的集合$\mathcal{H}\mathcal{CC}$是半零子句组成的集合$\mathcal{H}\mathcal{ZC}$的一个子集。其具体定义将会在下面给出。

回想一下：$\mathrm{FS}1$是所有$k$个变量的集合$S$的集合，使得$S$中没有两个变量在同一行或同一列。我们给$\mathrm{FS}1$中的每一个集合$S$分配一个半零子句$C_S$。首先，定义$S$-$\mathcal{C}\mathcal{T}\mathcal{A}$为给$S$中每个变量赋值为$1$的关键赋值的集合。（$\mathrm{FS}1$代表“fixed set of 1’s”，即$S$限定了关键赋值中的$k$个取值为$1$的变量）。接下来，令$S$-$\mathcal{H}\mathcal{ZC}$是所有能够代表$S$-$\mathcal{C}\mathcal{T}\mathcal{A}$中某一关键赋值的半零子句$C$的集合。根据引理2，集合$S$-$\mathcal{H}\mathcal{ZC}$非空。令$C_S$是$S$-$\mathcal{H}\mathcal{ZC}$中第一个在$R$中出现的子句。可以这么理解：对于集合$S$，找出所有使$S$中变量赋值为$1$的关键赋值，再找出所有能代表这其中某一关键赋值的半零子句，取其中在$R$中最早出现的子句即为$C_S$。注意，$C_S$的任何前驱子句都不可能出现在$S$-$\mathcal{H}\mathcal{ZC}$中。令 H C C = { C S ∣ S ∈ F S 1 } \mathcal{HCC}=\{C_S|S\in\mathrm{FS}1\} HCC={CS​∣S∈FS1}。

引理5 每个高复杂度子句都有至少$k+1$行，其中每行包含一个以否定形式出现的变量或至少$2k$个以肯定形式出现的变量。

证明：

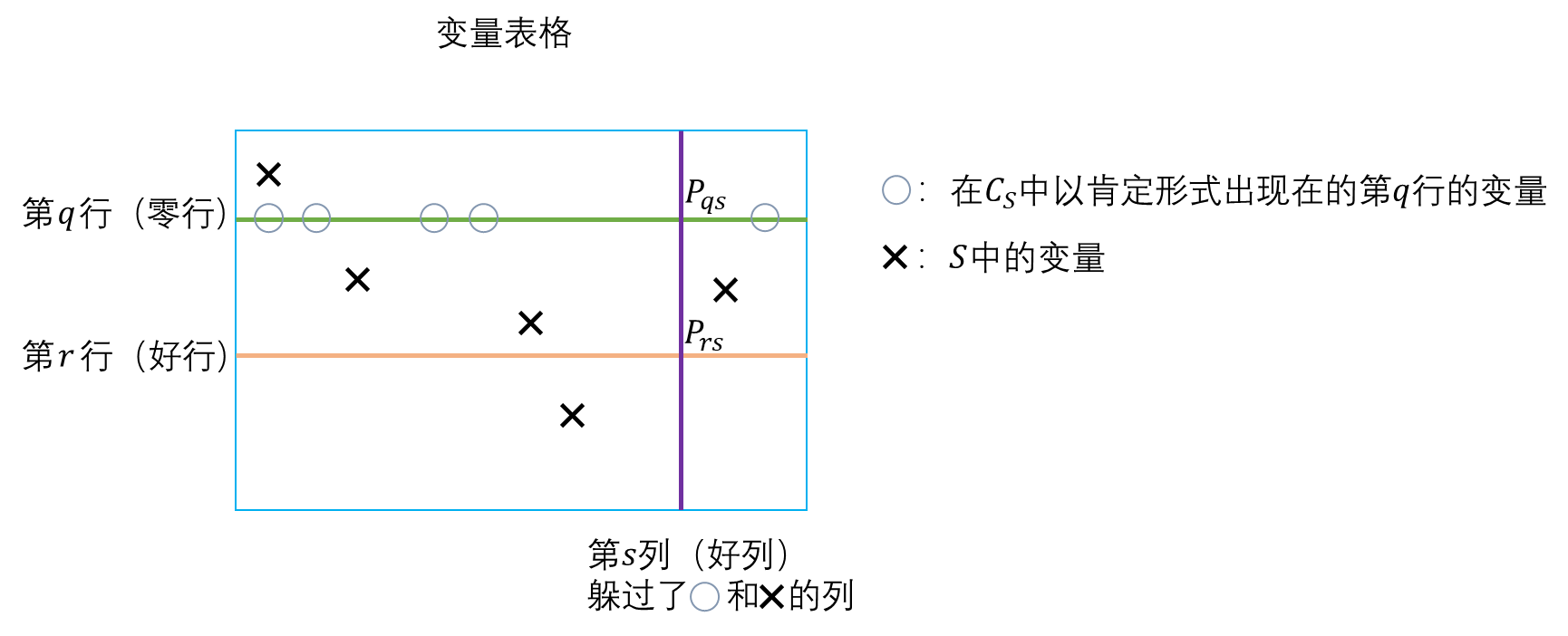
1. 设$S\in \mathrm{FS}1$并设$C_S$是对应的高复杂度子句。设$V$是被$C_S$代表的关键赋值，并设$V$的零行是第$q$行。由于$C_S$是半零子句，变量表格第$q$行有$2k$个变量在$C_S$中以肯定的形式出现，并且表格的$k$列有变量出现在$C_S$中。抛开这些列，还剩$n-1-3k\ge k$列（称为“好列”），好列的第$q$行的变量不在$C_S$中出现而且不包含在$S$中出现的变量。每个好列关于$V$对应于一个行，称为“好行”。（好行的定义）
2. 设$r$是一个好行，且令列$s$和行$r$关于$V$相对应。要么有第$r$行的某个变量在$C_S$中以否定的形式出现，要么$C_S$代表$V$的$r$-邻居$W$（根据引理4，如果第$r$行的所有变量都不以否定的形式在$C_S$中出现，再结合好列$s$第$q$行的变量$P_{qs}$不在$C_S$中出现，那么$C_S$就代表$V$的$r$-邻居$W$）。（好列的定义，引入$r$-邻居$W$）
3. 现在处理$C_S$代表$W$的情况。
   • 因为$V\in S$-$\mathcal{C}\mathcal{T}\mathcal{A}$，所以$S$中的每个变量必须在$V$中的赋值为$1$。因此，第$q$行的变量都不出现在$S$中。第$r$行的变量也都不出现在$S$中，因为第$r$行和第$s$列对应，第$r$行如果有$S$中的变量也一定是$P_{rs}$，但第$s$列是好列，所以不含$S$中的变量。这也就意味着，在$V$中交换$q$、$r$两行不改变$S$中变量的赋值。所以，$W\in S$-$\mathcal{C}\mathcal{T}\mathcal{A}$。（证明$W\in S$-$\mathcal{C}\mathcal{T}\mathcal{A}$）
   • 由于$C_S$是$S$-$\mathcal{H}\mathcal{ZC}$中第一个出现在$R$中的子句，而所有代表$W$的子句在$S$-$\mathcal{H}\mathcal{ZC}$中，因此$C_S$的任何前驱子句都不能代表$W$。$W$的零行为第$r$行，$C_S$代表$W$，用$C_S$和$W$套用引理3（注意“要么-要么”的第二个要么不成立，所以只有第一个要么成立），得：第$r$行必然有$2k$个变量以肯定的形式在$C_S$中出现。（分析$C_S$代表$W$的情况下好行的性质）
4. 回顾绿色句子，可知所有好行满足引理5中的条件。所以，第$q$行和所有的好行构成了引理5中提到的$k+1$行。（得到引理5中提到的$k+1$行）

示意图：

六、函数$f(n)$

回顾一下$h(n)=|\mathrm{FS}1|$。$\mathrm{FS}1$中的每个元素都对应一个高复杂度子句，但这个映射不一定是单射。我们需要给出一个高复杂度子句对应的$\mathrm{FS}1$中的元素的个数上界，该上界即为$g(n)$。

设$C\in \mathcal{H}\mathcal{CC}$。若$C$是对应于$\mathrm{FS}1$中某个元素$S$的$C_S$，那么$S$中的变量在$C$中要么不出现，要么以否定的形式出现（注意$C_S$代表了$S$-$\mathcal{C}\mathcal{T}\mathcal{A}$中的某个关键赋值，而这个关键赋值对$S$中元素的赋值为$1$）。根据引理1，$C_S$每行至多只有一个以否定形式出现的变量。我们用$C$的复杂性来限制在$\mathrm{FS}1$中选择$S$使得$C=C_S$的方案数。为了得到$g(n)$，我们数出给${\mathrm{PHP}}_n^{n-1}$的变量赋$k$个$1$的方案数，这些方案使得没有两个赋值为$1$的变量在同一行或同一列，$C$中以肯定形式出现的变量赋值为$0$，且如果某一行的一个变量在$C$中以否定形式出现，则这个变量是这一行唯一可以赋值为$1$的变量。每个这种赋$k$个$1$的方法对应$\mathrm{FS}1$中的一个$S$。

设$A$是引理5中提到的$C$的$k+1$行，其中每行包含一个以否定形式出现的变量或至少$2k$个以肯定形式出现的变量。对于$A$的每一行，我们至多可以给其中$n-1-2k$个变量赋值为$1$（如果该行有一个以否定形式出现的变量，则只能赋一个$1$；如果有$2k$个以肯定形式出现的变量，则可以赋$n-1-2k$个$1$）。当我们赋$k$个$1$的时候，存在一个数$i$使得其中$i$个$1$是在$A$的$k+1$行中出现的，剩余$k-i$个$1$是在除$A$之外的剩下$n-k-1$行中出现的。$i$可以是$0$到$i$的任意值。给定一个$i$，有$d_i$种方法选择含有$1$的行，其中$d_i=C_{k+1}^i{C}_{n-k-1}^{k-i}$。对于$A$中的$i$行，我们有至多${(n-1-2k)}^i$中方法选择$1$出现在哪一列（这个界很松，虽然我们应该考虑列不能重复，但我们不知道能选的$n-1-2k$列究竟是哪些列，所以也就无法避免重复的列了）。对于不在$A$中的行，我们至多有$A_{n-1-i}^{k-i}=\frac{(n-1-i)!}{(n-1-k)!}$种选法来选择$1$出现在哪一列，因为每一列只能用一次。所以，$$g(n)=\sum _{i=0}^k{d}_i{(n-1-2k)}^i\frac{(n-1-i)!}{(n-1-k)!}$$对于$h(n)=|\mathrm{FS}1|$，考虑选$k$个行，共有$C_n^k$种选法；再从$n-1$列中选$k$列，共有$A_{n-1}^k=\frac{(n-1)!}{(n-1-k)!}$种选法。所以$$h(n)=C_n^k{A}_{n-1}^k=C_n^k\frac{(n-1)!}{(n-1-k)!}$$利用组合数恒等式$C_n^k=\sum _{i=0}^k{C}_{k+1}^i{C}_{n-k-1}^{k-i}=\sum _{i=0}^k{d}_i$（可理解为：先在$k+1$个中选$i$个，再在$n-k-1$个中选$k-i$个），我们得到$$h(n)=\sum _{i=0}^k{d}_i\frac{(n-1)!}{(n-1-i)!}\frac{(n-1-i)!}{(n-1-k)!}$$所以$$f(n)=\frac{h(n)}{g(n)}=\frac{\sum _{i=0}^k{d}_i}{\sum _{i=0}^k{d}_i\frac{(n-1-i)!{(n-1-2k)}^i}{(n-1)!}}$$令$n\ge 201$。考虑放大$\frac{(n-1-i)!{(n-1-2k)}^i}{(n-1)!}$。当$i\le k$时，$\frac{n-1-2k}{n-1-i}\le \frac{n-1-2k}{n-1-k}\le \frac{2k+1}{3k}<\frac{1}{1.49}$，故${(n-1-2k)}^i\le \frac{{(n-1-i)}^i}{{1.49}^i}$。因此$\frac{(n-1-i)!{(n-1-2k)}^i}{(n-1)!}\le \frac{(n-1-i)!{(n-1)}^i}{(n-1)!{1.49}^i}=\frac{(n-i)\cdot (n-i)\cdot \cdots \cdot (n-i)}{(n-1)\cdot (n-2)\cdot \cdots \cdot (n-i)}\frac{1}{{1.49}^i}\le 1\cdot \frac{1}{{1.49}^i}=\frac{1}{{1.49}^i}$。于是我们有$$f(n)>\frac{\sum _{i=0}^k{d}_i}{\sum _{i=0}^k\frac{d_i}{{1.49}^i}}(\ast )$$令$m=\lfloor \frac{n-1}{50}\rfloor$。当$i+1\le 2m$时，$$\frac{d_{i+1}}{d_i}=\frac{(k+1-i)(k-i)}{(i+1)(n-2k+i)}>\frac{[(n-1)/5][(n-1)/5]}{[(n-1)/25][0.6(n-1)]}>1.5$$故$$\sum _{i=0}^{m-1}\frac{d_i}{{1.49}^i}\le \sum _{i=m}^{2m-1}\frac{d_i}{{1.49}^i}(†)$$考虑$(\ast )$式不等号右端的分式，记分子为$\Phi$，分母为$\Psi$。对分母$\Psi$应用$(†)$式并放大得$$\Psi =\sum _{i=0}^k\frac{d_i}{{1.49}^i}\le \left(2\sum _{i=m}^{2m-1}+\sum _{i=2m}^k\right)\frac{d_i}{{1.49}^i}<2\sum _{i=m}^k\frac{d_i}{{1.49}^i}<2\sum _{i=m}^k\frac{d_i}{{1.49}^m}$$对分母缩小得$$\Phi =\sum _{i=0}^k{d}_i>\sum _{i=m}^k{d}_i$$于是$$f(n)>\frac{\sum _{i=m}^k{d}_i}{2\sum _{i=m}^k\frac{d_i}{{1.49}^m}}=\frac{{1.49}^m}{2}>{({1.49}^{0.01})}^n$$所以，对于任意$n\ge 201$，$f(n)>c^n$，其中$c={1.49}^{0.01}$。
$\text{Q.E.D.}$

值得注意的是，虽然命题鸽巢原理有指数级归结下界，但它有多项式大小的弗雷格证明（Buss 1987^[2]）和扩展弗雷格证明（Cook 1976^[3]）。它的指数级归结下界不能说明它太难，只能说明归结证明系统太弱。

参考文献

[1] Haken, Armin. “The Intractability of Resolution.” Theor. Comput. Sci. 39 (1985): 297-308.
[2] Buss, Samuel R. “Polynomial size proofs of the propositional pigeonhole principle.” Journal of Symbolic Logic 52 (1987): 916 - 927.
[3] Cook, Stephen A. “A short proof of the pigeon hole principle using extended resolution.” SIGACT News 8 (1976): 28-32.