二、时间序列介绍

        时间序列通常是在固定采样间隔内随时间顺序测量的变量，从而产生时间序列形式的数据。时间序列最重要的特征之一是时间上接近的观察结果往往是相关的（序列相关）。基本上，我们基于这种序列依赖性进行所有预测，从经典的 SARIMA 模型到 LSTM 或 LGBT。时间序列中最重要的概念是趋势，季节性、周期、随机游走和白噪声。

        趋势是时间序列中的系统性变化，看起来不具有周期性。相反，季节性变化是每个时期（无论采样间隔是年、月、周等）内的重复模式，并且可以在更多采样周期内重复自身。周期是一种与某些固定采样间隔不对应的模式，但它具有相同的重复模式（例如米兰科维奇周期、厄尔尼诺现象、商业周期……）。白噪声是时间序列中的纯粹随机性，当我们删除所有模式（趋势、季节性、自相关）时留下的。白噪声应该与此处定义的随机游走区分开来，并且它不是平稳过程，因为它与时间无关。

        让我们看一个示例，使用非常简单且有用的包 statsmodels 来分解时间序列 - 如何提取趋势和季节性以及如何检查时间序列是否平稳。所有这些使我们能够进行预测，基本上假设现有的时间序列模式将在某个（至少）较短的未来时间继续（推断）。我们将使用可以在此处找到的著名的航空乘客数据。

航空旅客数据

三、趋势和季节性示例

        现在我们将时间序列分解为趋势和季节（将采用 12 个月的输入参数）。之后我们必须检查残差的平稳性。平稳时间序列是一种其属性不依赖于观察该序列的时间的序列。因此，具有趋势或季节性的时间序列并不是静止的——趋势和季节性会影响时间序列在不同时间的值。另一方面，白噪声序列是平稳的——什么时候观察它并不重要，它在任何时间点看起来都应该大致相同。因此，我们将检查残差的平稳性，这表明我们确实做了趋势和季节性解释了时间序列的所有“模式”。

from statsmodels.tsa.seasonal import seasonal_decomposedef decomposition(timeseries, period):decomposition = seasonal_decompose(timeseries, period=period)trend = decomposition.trendseasonal = decomposition.seasonalresidual = decomposition.residplt.figure(figsize=(10, 5))plt.subplot(411)plt.plot(timeseries, label='Original')plt.legend(loc='best')plt.subplot(412)plt.plot(trend, label='Trend')plt.legend()plt.subplot(413)plt.plot(seasonal,label='Seasonality')plt.legend()plt.subplot(414)plt.plot(residual, label='Residuals')plt.legend()plt.tight_layout()plt.show(block=False)
decomposition(data, 12)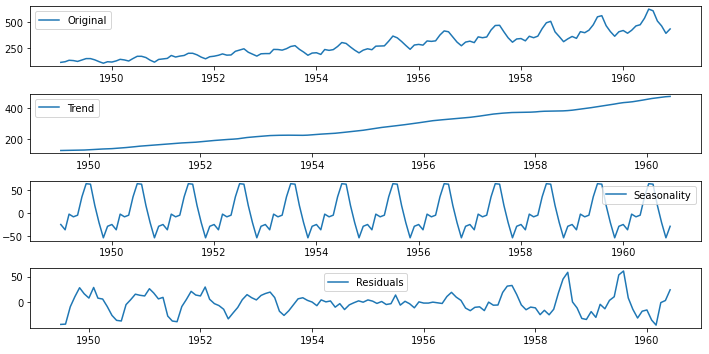

 时间序列的分解

        我们将使用 adfuller 检验来告诉我们零假设是否为真（时间序列不是平稳的）。

from statsmodels.tsa.stattools import adfuller
def test_stationarity(timeseries, rolling=12):#Determing rolling statisticsrolmean = timeseries.rolling(rolling).mean()rolstd = timeseries.rolling(rolling).std()#Plot rolling statistics:plt.figure(figsize=(10, 5))orig = plt.plot(timeseries, color='blue',label='Original')mean = plt.plot(rolmean, color='red', label='Rolling Mean')std = plt.plot(rolstd, color='black', label = 'Rolling Std')plt.title('Power consumption Old data')plt.xlabel('Time - periods(30s)')plt.ylabel('Power consumption in Watts')plt.legend(loc='best')plt.title('Rolling Mean & Standard Deviation')plt.show()#Perform Dickey-Fuller test:print ('Results of Dickey-Fuller Test:') dftest = adfuller(timeseries, autolag='AIC')dfoutput = pd.Series(dftest[0:4], index=['Test Statistic','p-value','#Lags Used','Number of Observations Used'])for key,value in dftest[4].items():dfoutput['Critical Value (%s)'%key] = valueprint (dfoutput)if dfoutput['p-value'] < 0.05:print('The timeseries is stationary at 95% level of confidence')else:print('The timeseries is not stationary at 95% level of confidence')
test_stationarity(data, rolling=12)

时间序列平稳性检验结果

        从结果中可以看出，残差不是平稳的，并且您可以看到标准差如何随着时间的推移而增加，这意味着时间序列中还有一些参数需要额外分析。这导致了自回归参数和移动平均线。另外，我们显然在这个时间序列中具有乘性季节性效应，这意味着季节性效应随着趋势的增加而增加（Xt = mt（趋势）* st（季节）+ zt（误差））。但是让我们注意自回归。

        自回归可以很容易地理解为自相关，即时间序列与其自身在其他时间点的相关性。为此，我们使用相关图来显示不同时间点的去季节和去趋势时间序列的相关性。作为参数，我们可以输入要计算自相关的滞后数（在此数据中，我们有 144 个时间点）。

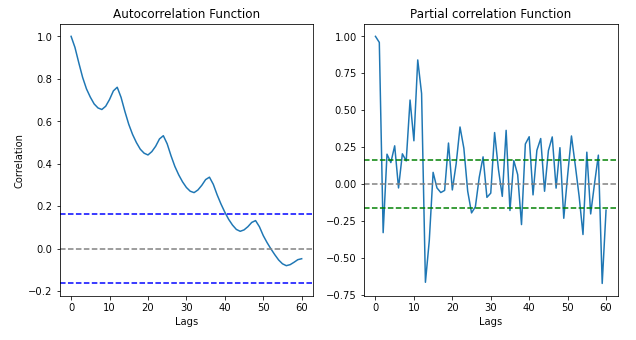
        蓝色和绿色线是我们的时间序列的时间滞后的相关性和部分相关性的置信水平。

        通常，如果 ACF 和 PACF 正在缓慢衰减，则意味着我们必须再做一件事，那就是求差。这应该有助于我们获得残差的平稳性，这在实践中意味着我们解释了时间序列的所有组成部分，并且我们完全“阅读”了它的模式。差分减去两个最接近的时间点。

def differencing(timeseries, second_order=False):diff = timeseries - timeseries.shift(1)diff=diff.dropna()print('Results of stationarity of the first ordered differencing')test_stationarity(diff)if second_order:diff_sec = diff - diff.shift(1)diff_sec=diff_sec.dropna()print('\n', 'Results of stationarity of the SECOND ordered differencing')test_stationarity(diff_sec)
differencing(data, False)

一阶差分并没有使时间序列平稳。

        在这里我们可以看到一阶差分还没有导致平稳时间序列。我们将尝试二阶差分（已差分时间序列的差分）。

differencing(data, True)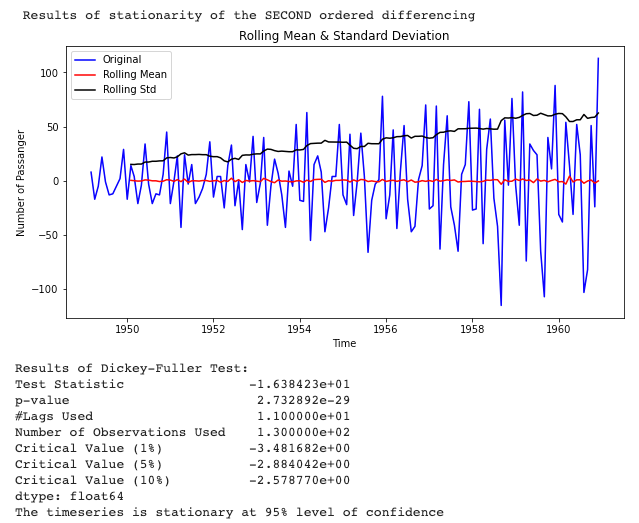

二阶差分导致时间序列的平稳性。

        最后！我们得到了平稳残差。残差的平均值和标准差不随时间变化。这意味着我们在 ARIMA 中的 I 参数应该是 2。但是 AR 和 MA 呢？正如您所猜测的，AR 是自回归参数，而 MA 是移动平均线。阅读上面的相关图，我们可以得出采用哪些参数的结论。公认的规则是，我们有 ACF 的正弦模式，并且在 PACF 中跳跃，它应该是 AR = 2，这意味着我们的预测时间点将采用以下公式： Yt = b0 + b1 Yt-1 + b2 Yt-2 + wt ( wt =白噪声）。维托米尔·约万诺维奇