矩阵理论——Gerschgorin定理，以及用python绘制Gerschgorin圆盘动图

在矩阵的特征值估计理论当中，有一节是盖尔圆盘定理：

对于一个n阶复数矩阵A，每个特征值lambda位于至少一个Gerschgorin圆盘中，这些圆盘的中心为矩阵A的对角线元素aii，半径为该行（或列）的非对角线元素的绝对值之和：

D(i) = {z ∈ C : |z - a_ii| ≤ Σ|a_ij|, j ≠ i}

其中，D(i)表示第i个Gerschgorin圆盘，aii表示矩阵A的第i行（或第i列）的对角线元素，aij表示矩阵A的第i行（或第i列）的非对角线元素。

根据Gerschgorin定理，可以得出以下结论：

1. 矩阵A的所有特征值都位于所有Gerschgorin圆盘的并集内。
2. 如果某个Gerschgorin圆盘不与其他任何圆盘有交集，则该圆盘内至少有一个特征值。
3. 如果k个Gerschgorin圆盘连通，则连通区域中有且仅有k个特征值。此时可能有的圆盘没有特征值。

为了更好的理解这个定理，用python绘制动图，将更好理解这个过程。

其中:
$$A=\left[\begin{array}{cc}1& -0.8\\ 0.5& 0\end{array}\right]=B+D=\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right]+\left[\begin{array}{cc}0& -0.8\\ 0.5& 0\end{array}\right]$$

$$A(\epsilon )=B+\epsilon D=\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right]+ϵ\left[\begin{array}{cc}0& -0.8\\ 0.5& 0\end{array}\right]$$

动图：

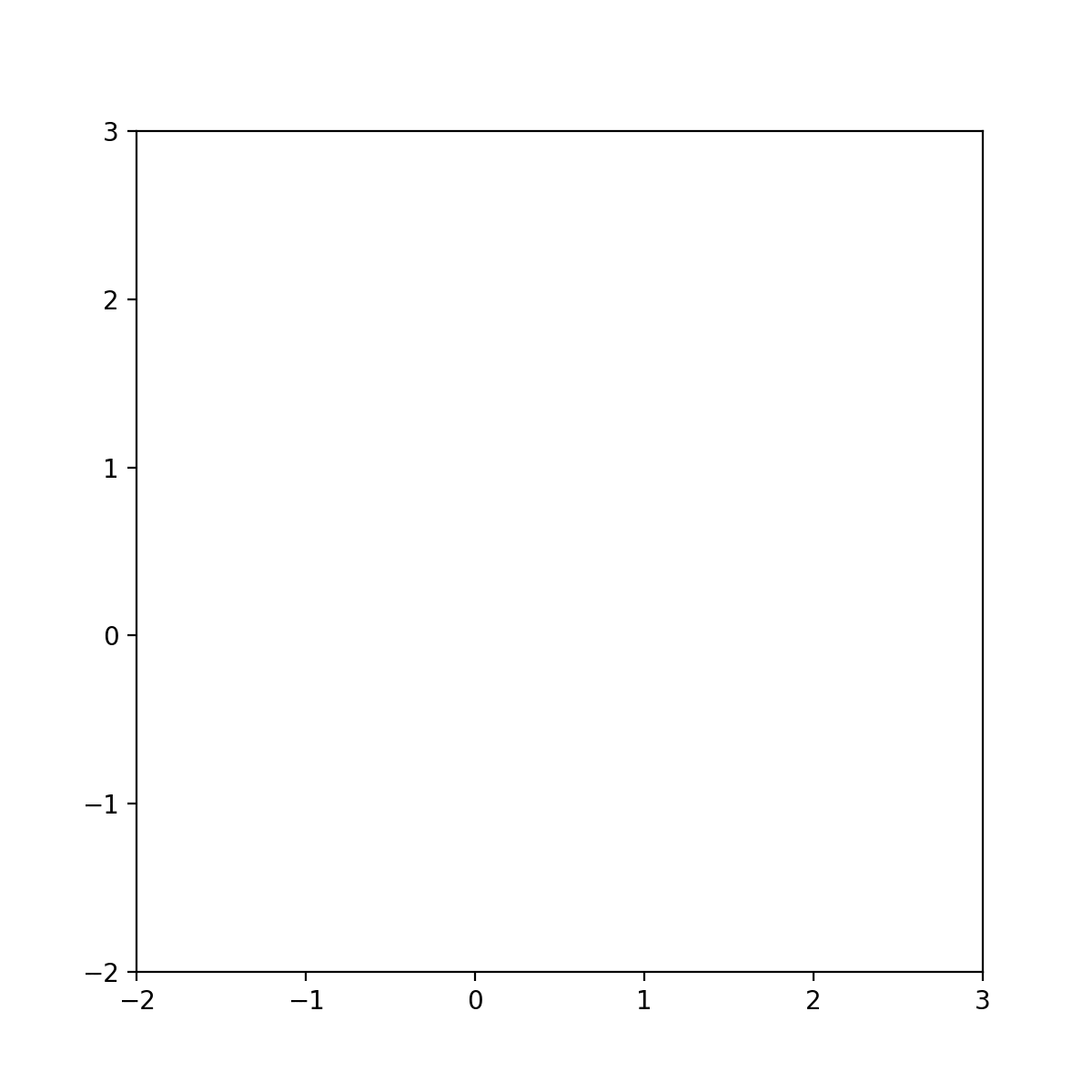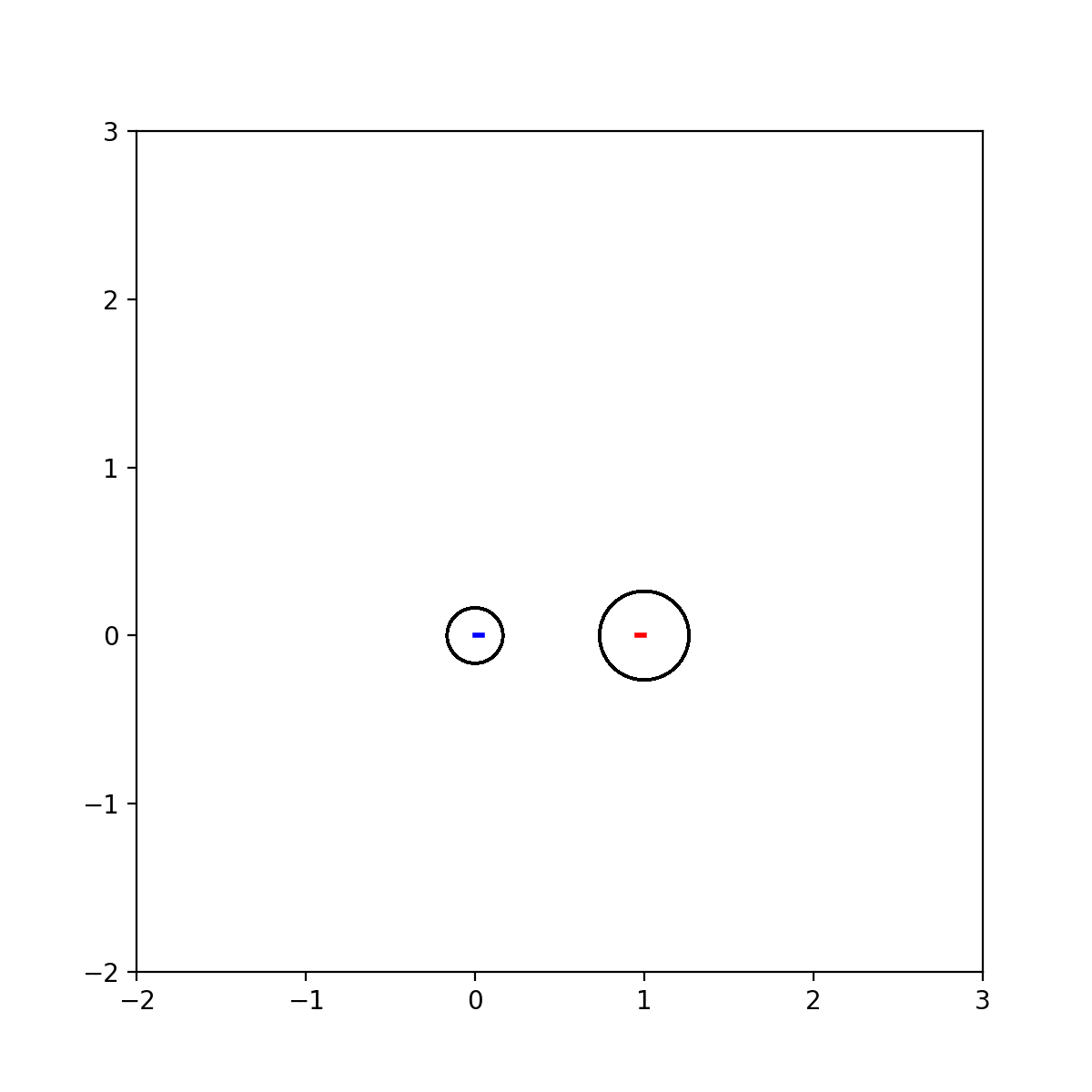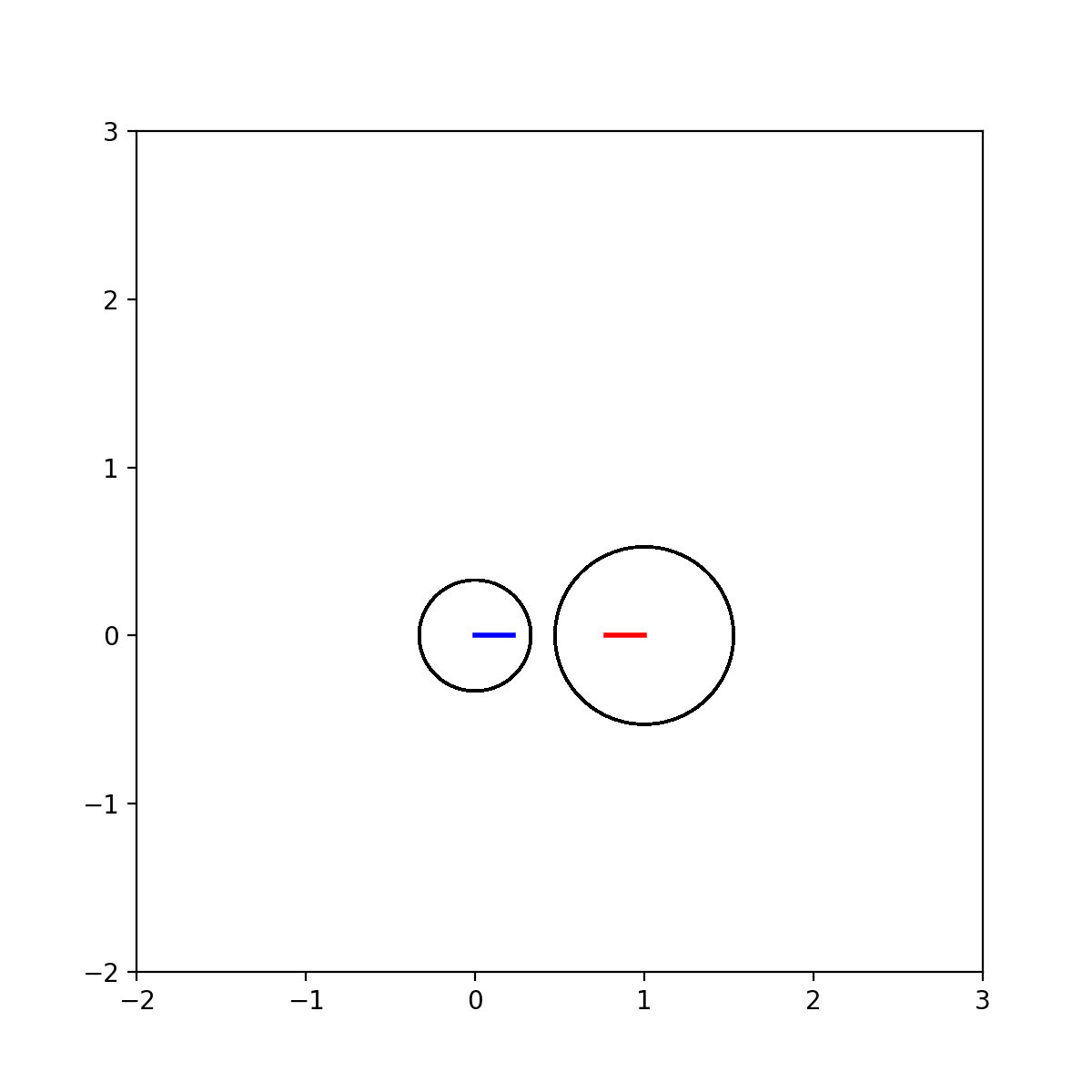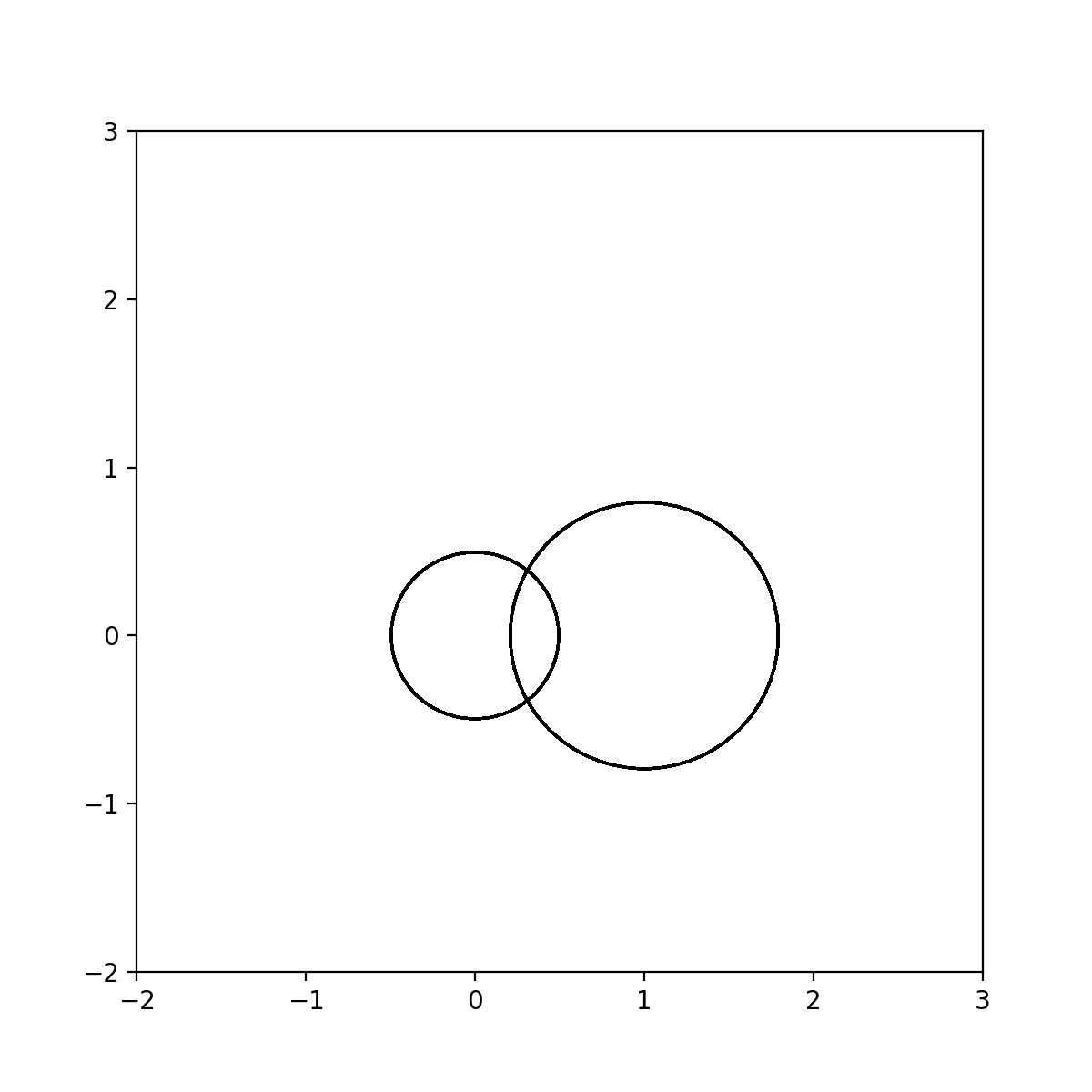
代码：

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Mon Nov 20 13:48:19 2023@author: wangshouguo
"""
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation# 创建一个图形窗口
fig = plt.figure(figsize=(6, 6))
ax = plt.gca()
# 设置坐标轴范围
ax.set_xlim(-2, 3)
ax.set_ylim(-2, 3)# 初始化两个空的圆对象
circle1 = plt.Circle((0, 0), 0.1, edgecolor='black', facecolor='none')
circle2 = plt.Circle((1, 0), 0.1, edgecolor='black', facecolor='none')# 初始化两条空的线对象
line1, = ax.plot([], [], 'r-', lw=2)
line2, = ax.plot([], [], 'b-', lw=2)x1,y1,x2,y2 = [],[],[],[]# 初始化函数，用于绘制每一帧的内容
def init():ax.add_patch(circle1)ax.add_patch(circle2)line1.set_data([], [])line2.set_data([], [])return circle1, circle2, line1, line2# 更新函数，用于更新每一帧的内容
def update(frame):delta = frame/100;radius1 = 0.5*deltaradius2 = 0.8*deltaB = np.array([[1,0],[0,0]])D = np.array([[0,-0.8],[0.5,0]])A = B+D*deltaa,b = np.linalg.eigvals(A)circle1.center = (0, 0)circle1.set_radius(radius1)circle2.center = (1, 0)circle2.set_radius(radius2)x1.append(np.real(a))y1.append(np.imag(a))x2.append(np.real(b))y2.append(np.imag(b))line1.set_data(x1, y1)line2.set_data(x2, y2)if frame==99:x1.clear()x2.clear()y1.clear()y2.clear()return circle1, circle2, line1, line2# 创建动画对象
ani = FuncAnimation(fig, update, frames=100, init_func=init,interval=20, blit=True)# 显示动画
plt.show()