目录
- Why Ray Tracing?(为什么需要光线追踪?)
- Basic Ray Tracing Algorithm(基础的光线追踪算法)
- Ray Casting(光线的投射)
- Generating Eye Rays(生成Eye Rays)
- Recursive(Whitted-Styled) Ray Tracing
- Ray-Surface Intersection(光线和平面的交点)
- Ray Rquation(射线方程)
- Ray Intersection With Sphere(光线和球体求交)
- Ray Intersection With Implicit Surface(光线和隐式曲面求交)
- Ray Intersection With Triangle Mesh(光线和三角网格求交)
- Ray Intersection With Triangle(光线与三角形求交)
- Moller Trumble Algorithm
- Accelerating Ray-Surface Intersection(加速光线和曲面求交)
- Bounding Volumes(包围盒)
- Ray Intersection With Axis-Aligned Box(光线与AABB求交)
- Why Axis-Aligned?
- 参考资料
Why Ray Tracing?(为什么需要光线追踪?)
- 光栅化不能很好地表示全局的效果
- 软阴影
- 光线反弹超过一次(间接光照)
- 光栅化很快,但是质量不高
- 光线追踪是一种准确的方法,但是非常慢
- 光栅化:实时;光线追踪:离线

Basic Ray Tracing Algorithm(基础的光线追踪算法)
关于光线的三个想法:
- 光线是沿直线传播的
- 光线和光线不会发生碰撞
- 光线从光源发射出来后经过传播后到达眼睛。
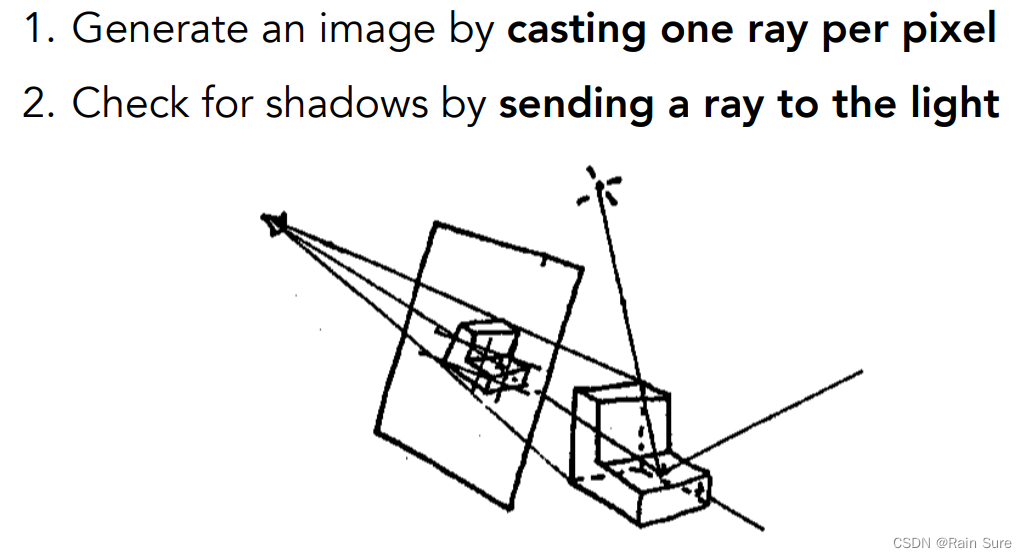
Ray Casting(光线的投射)
- 从相机出发,生成一张图片通过投射每个像素。
- 将物体每个点连接一条光线到光源,通过计算能量来进行着色。
Generating Eye Rays(生成Eye Rays)
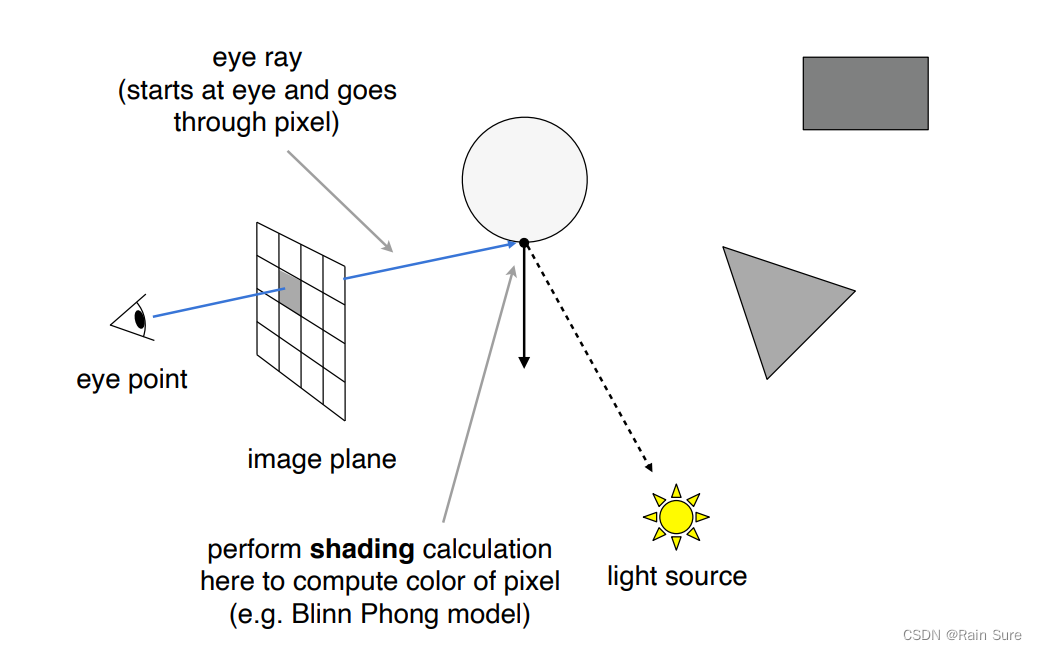
针孔相机模型:
- 从摄像机发出一条光线,打到场景中最近的物体上的某个点上。
- 将该点与光源进行连线,这跟光线称作shadow ray
- 如果这条光线没有被其它物体挡着,我们就认为这个点对光源可见。
- 有了法线,入射方向和出射方向,我们就可以算出这一点的着色(Blinn Phong模型),然后写入像素。
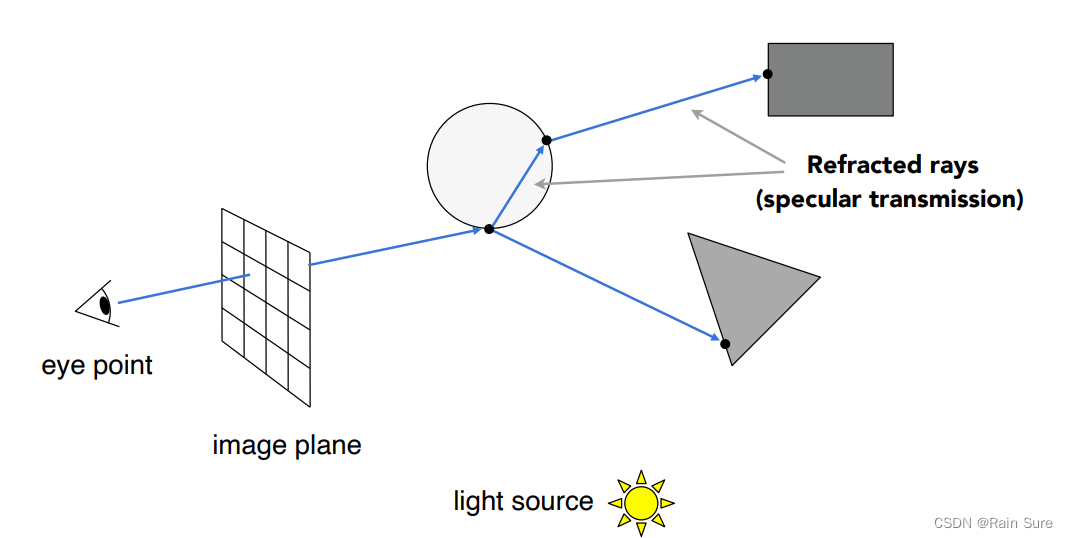
Recursive(Whitted-Styled) Ray Tracing
与上面的模型不同,Whitted光线追踪模型中,一个光线在打到一个物体后可以继续传播,我们只需要知道它的折射方向和反射方向的参数。
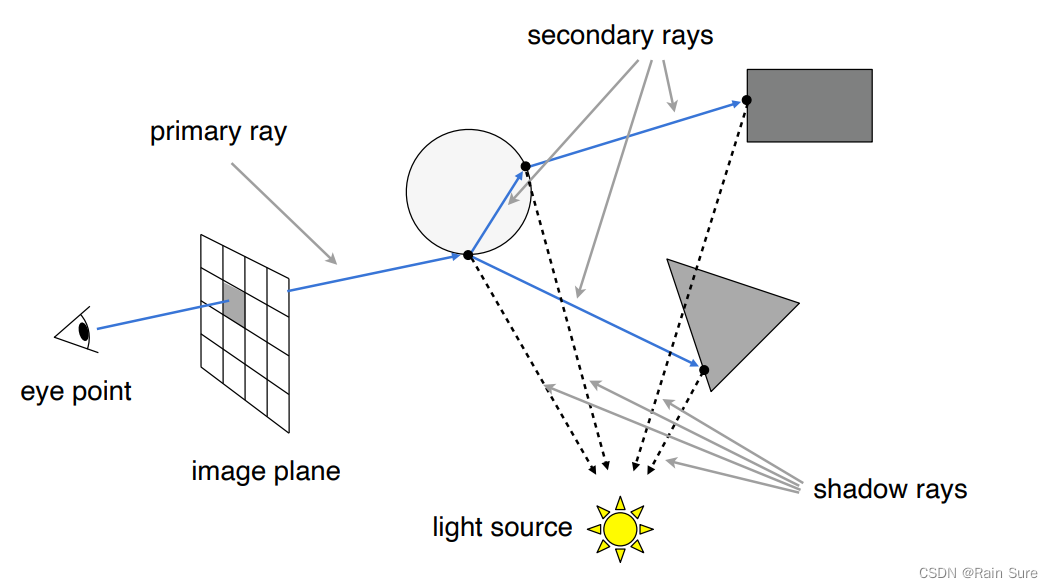
在光线传播中遇到的每个点,都和光线连一条光线判断是否能被光源照亮。
如何光源可以照亮某个点,我们就把这个点的着色算出加到像素的最终着色值上去。
Ray-Surface Intersection(光线和平面的交点)
Ray Rquation(射线方程)
一条光线由起点和传播方向就可以定义。
射线方程:
r ( t ) = o + t d , 0 ≤ t < ∞ r(t) = o + td , 0 \leq t \lt \infty r(t)=o+td,0≤t<∞
Ray Intersection With Sphere(光线和球体求交)
球体方程:
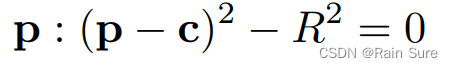
其中, p p p是球面上的点, c c c是球心, R R R是半径。
交点一定同时满足光线的射线方程和球体方程。
可以通过求解方程得到交点:
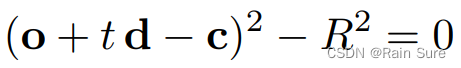
通过二次函数求根公式,得到解:
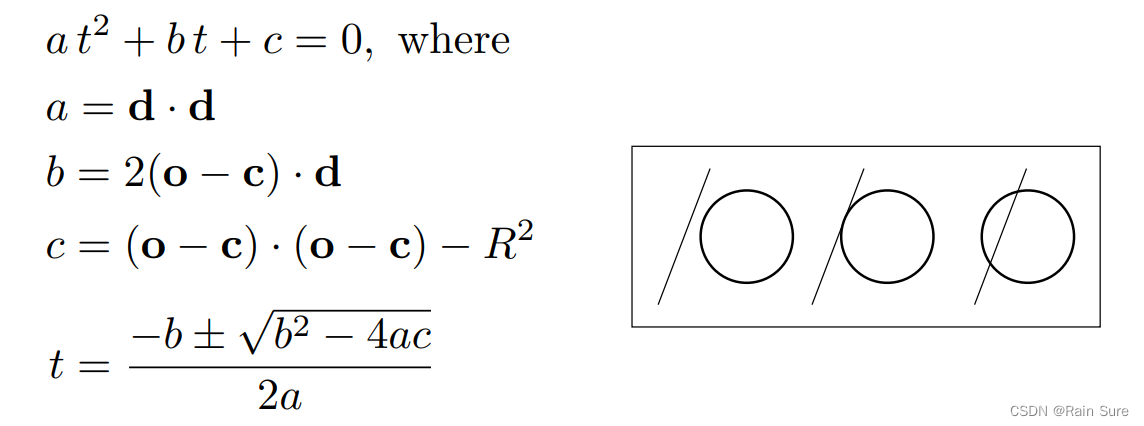
Ray Intersection With Implicit Surface(光线和隐式曲面求交)
联立光线射线方程和曲面的隐式方程求解即可,注意解需要满足是实数并且是正数。

Ray Intersection With Triangle Mesh(光线和三角网格求交)
需求:
- 渲染:可视性、阴影、光照
- 几何:内部/外部测试,如果一个点在物体内部,那么令该点向四周发射光线,交点数一定是奇数。
如何求交呢?
可以将光线与三角网格中的每个三角形分别求交,最后取 t t t最小的值即可。
十分简单,但是效率非常低。
Ray Intersection With Triangle(光线与三角形求交)
三角形是一个平面,可以首先将光线与该平面求交,然后判断交点是否在三角形内部。
平面方程:
我们可以定义成法线 N N N和一个平面经过的某个点 p ′ p' p′的组合。
平面方程定义如下:
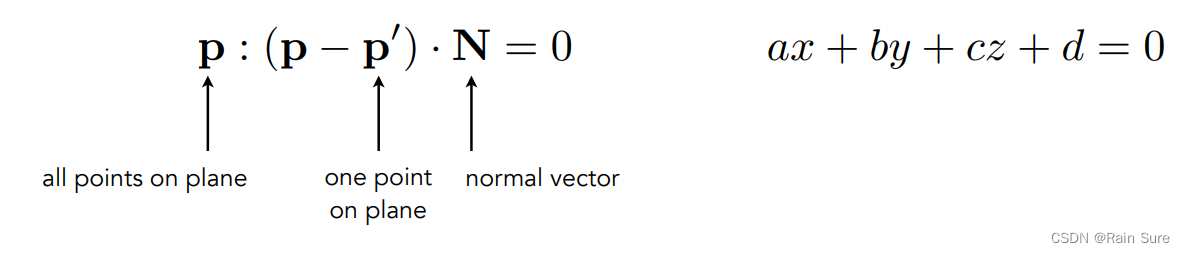
联立光线和平面的方程,求解得到交点:
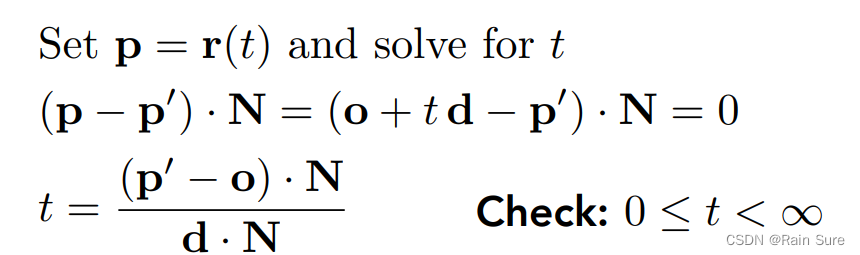
Moller Trumble Algorithm
这个算法可以一步到位地算出光线是否与三角形求交,主要利用的知识是三角形的重心坐标。

Accelerating Ray-Surface Intersection(加速光线和曲面求交)
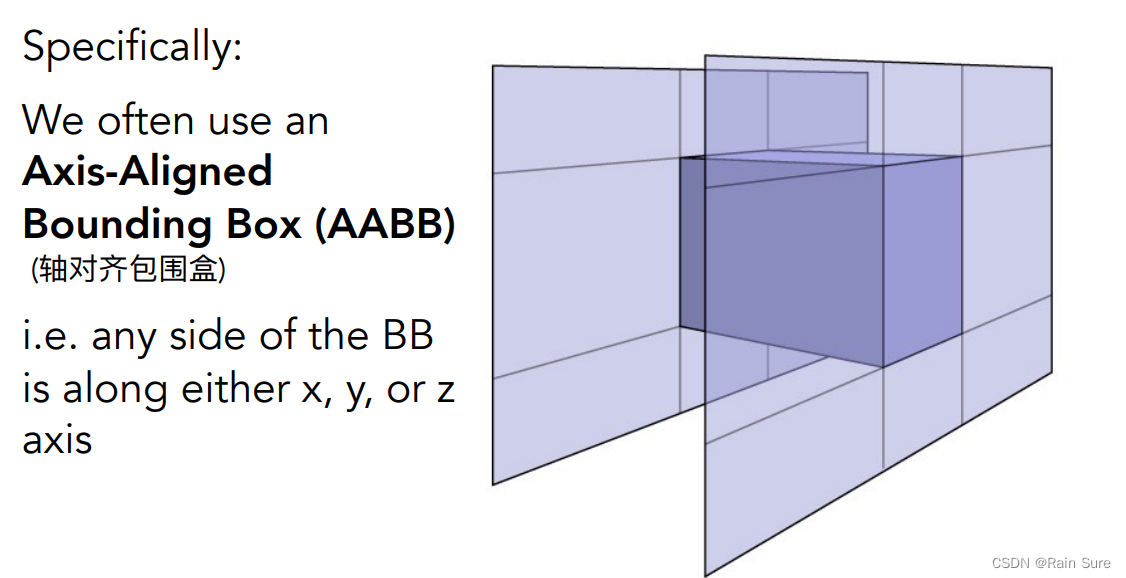
Bounding Volumes(包围盒)
包围盒是一个非常快速的方法来避免求交:将一个复杂的物体用一个简单的包围盒包围起来。
- 物体被完全包围在包围盒中。
- 如果光线连包围盒都不相交,那么一定不和物体求交。
- 所以,首先判断是否与包围盒相交,然后再判断是否和物体相交。
包围盒是三个不同的对立面形成的交集:
Ray Intersection With Axis-Aligned Box(光线与AABB求交)
考虑二维情况,三维同理。
分别考虑每一对面,计算出在最近和最远的交点。
t m i n t_{min} tmin取最大值得到 t e n t e r t_{enter} tenter, t m a x t_{max} tmax取最小值得到 t e x i t t_{exit} texit。
关键思想:
只有当光线全部进入所有对立面的时候,才是真正进入包围盒。
只要光线出任意一个对立面时,光线就穿出包围盒了。
如果 t e n t e r < t e x i t t_{enter} < t_{exit} tenter<texit,光线就和包围盒有交点。
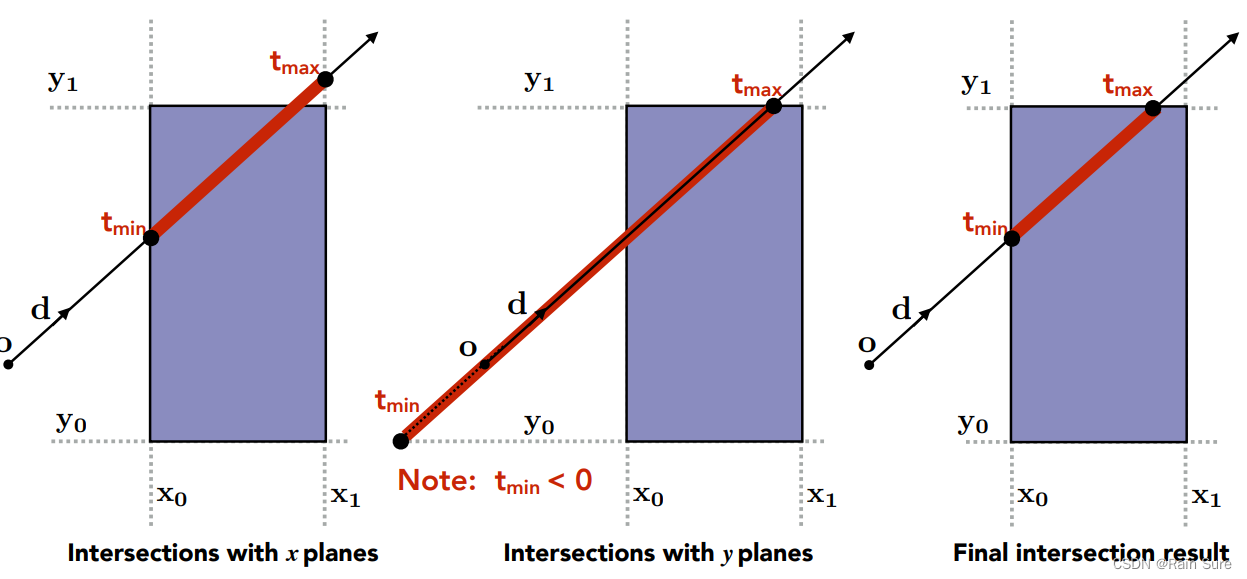
考虑两种特殊情况:
- 如果 t e x i t < 0 t_{exit} < 0 texit<0:
包围盒在光源的后面。 - 如果 t e x i t ≥ 0 , t e n t e r < 0 t_{exit} \geq 0, t_{enter} \lt 0 texit≥0,tenter<0:
光源在包围盒的内部。
Why Axis-Aligned?
选择轴对齐的包围盒,可以使得求交点更简单。
参考资料
GAMES101 Lecture13
)
)



)













