什么是动态规划?
动态规划算法的基本思想-求解步骤-基本要素和一些经典的动态规划问题【干货】-CSDN博客
一、三步问题
面试题 08.01. 三步问题 - 力扣(LeetCode)

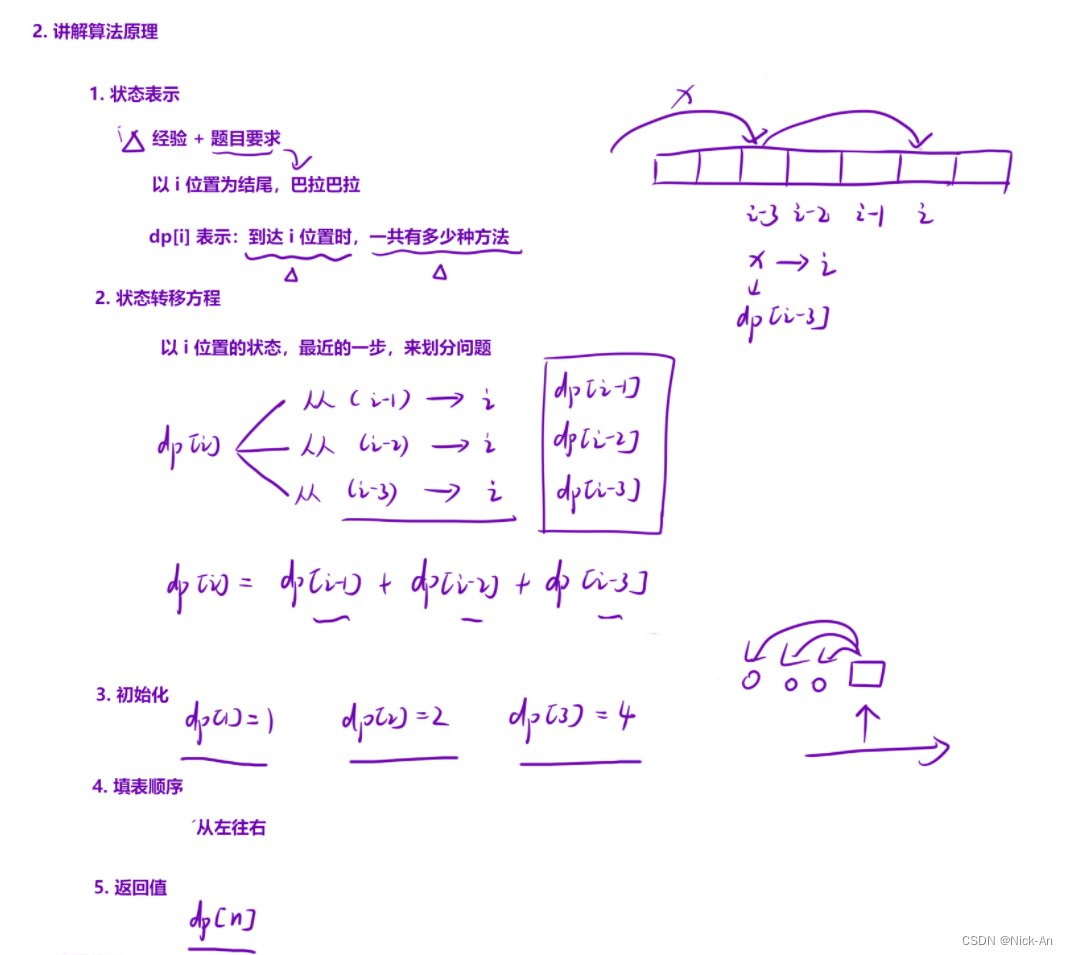
思路
我们要知道,走楼梯,前三个阶梯步数已经知道,那我们若是想走到第四楼,还需要一个个推吗?
走到4层,我们有三种方法
1.从一楼出发,这样只需要走3层即可。
2.从二楼出发,这样只需要走2层即可。
3.从三楼出发,这样只需要走1层即可。
所以在此问题中,我们要找到到达n个阶梯时,离n个阶梯最近的n-1,n-2,n-3的阶梯的最短路径。并且以此来递推出走到第n个阶梯的最短距离。
代码
int waysToStep(int n) {const int MOD=1e9+7;if(n==1||n==2) return n;if(n==3) return 4;vector<int> dp(n+1);dp[1]=1,dp[2]=2,dp[3]=4;for(int i=4;i<=n;i++){dp[i]=((dp[i-1]+dp[i-2])%MOD+dp[i-3])%MOD;}return dp[n];}二、使用最小花费爬楼梯
LCR 088. 使用最小花费爬楼梯 - 力扣(LeetCode)

思路
这也是个动态规划的题目,从底层楼梯爬到最上层,那我们建立表呢?
——设一个dp表,dp[i]表示到第i层需要花费的最少的钱。

由于付一次钱,就可以爬一层或者两层楼梯,所以我们需要比较的是到第i-1层和到第i-2层最小的值————min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]) 因此这就是我们的状态转移方程。
状态转移方程就是要把握到达每一步的值从哪里来?——然后比较出最小的那一步的值,依次类推,最后得出到达第i层最小的值。
代码
int minCostClimbingStairs(vector<int>& cost) {int len=cost.size();vector<int> dp(len+1);if(len==1) return cost[0];if(len==2) return min(cost[0],cost[1]);//返回两个中的最小值dp[0]=0,dp[1]=0;for(int i=2;i<=len;i++){dp[i]=min(cost[i-1]+dp[i-1],dp[i-2]+cost[i-2]);}return dp[cost.size()];}三、解码方法
91. 解码方法 - 力扣(LeetCode)

思路
这里我们知道判断就只有两个,一个是单个数字,一个是两个数字,所以我们也可以按照动态规划的方式,由第n-1个和第n-2个推出第n个的值。
代码
int numDecodings(string s) {int n=s.size();vector<int> dp(n+1);dp[0]=1;for(int i=1;i<=n;i++){if(s[i-1]!='0') dp[i]+=dp[i-1];//单个字母不为0,那么就往上加,一个字母就往前加一个if(i>1&&s[i-2]!='0'&&(s[i-2]-'0')*10+(s[i-1]-'0')<=26) dp[i]+=dp[i-2];//两个字母就加前两个的}return dp[n];}四、不同路径
LCR 098. 不同路径 - 力扣(LeetCode)

思路
首先,我们知道,只能向右或者向下行走,那么我们可以通过动态规划得出转移方程
dp[i][j]=dp[i][j-1]+dp[i-1][j],其中dp表代表的是到达i处的路径数。
初始化呢?——第一行和第一列都只有1,然后通过状态转移方程即可得出最后一个位置的值,也就是打到终点的路径数。
代码
int uniquePaths(int m, int n) {vector<vector<int>> dp(m, vector<int>(n));if(m==1&&n==1)return 1;for (int i = 1; i < n; i++){dp[0][i] = 1;}for (int i = 1; i < m; i++){dp[i][0] = 1;}for (int i = 1; i < m; i++)for (int j = 1; j < n; j++)dp[i][j] = dp[i - 1][j] + dp[i][j - 1];return dp[m - 1][n - 1];
}五、不同路径II
63. 不同路径 II - 力扣(LeetCode)
思路
思路和不同路径的思路一样,只不过需要判断障碍物的位置,若是有障碍物,那么就直接将障碍物所在的dp表的值定为0,表明到此位置的路径数为0,无法到达。
代码
int numDecodings(string s) {int n=s.size();vector<int> dp(n+1);dp[0]=1;for(int i=1;i<=n;i++){if(s[i-1]!='0') dp[i]+=dp[i-1];//单个字母不为0,那么就往上加,一个字母就往前加一个if(i>1&&s[i-2]!='0'&&(s[i-2]-'0')*10+(s[i-1]-'0')<=26) dp[i]+=dp[i-2];//两个字母就加前两个的}return dp[n];}











)






