组件间通讯 Vuex

https://vuex.vuejs.org/zh/

基本原理

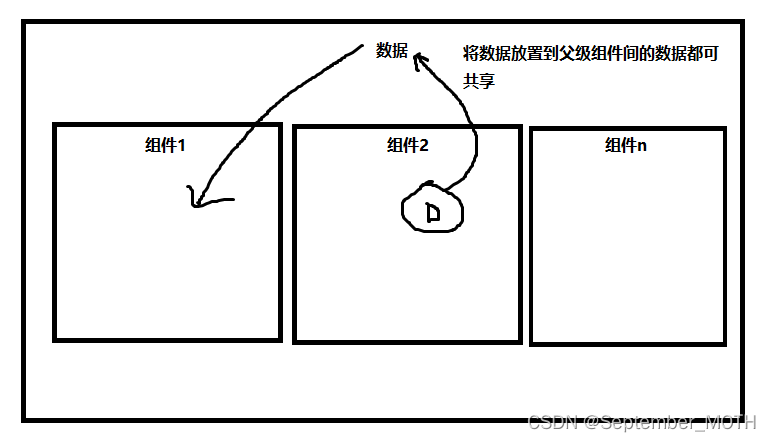
数据提取到父级

// index 文件
import Vue from 'vue'
import Vuex from "vuex"
import tab from './tab' // 引入 modulesVue.use(Vuex) // 全局引入// 创建 Vuex 实例
export default new Vuex.Store({modules: {tab}
})

// tab 模块
export default {state: {isCollapse: false // 控制菜单的展开还是收起},mutations: {// 修改菜单展开收起collapseMenu(state) { state.isCollapse = !state.isCollapse;}}}

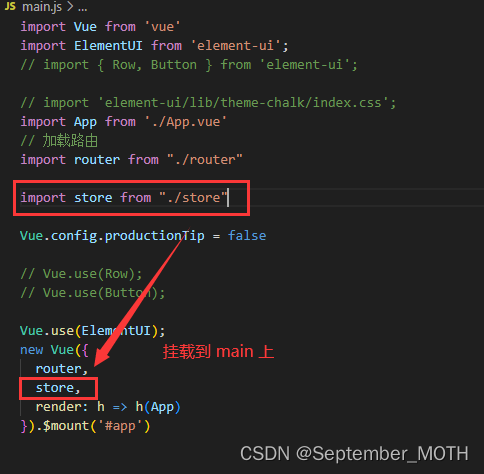
挂在到 min 上

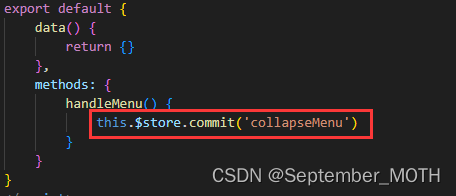
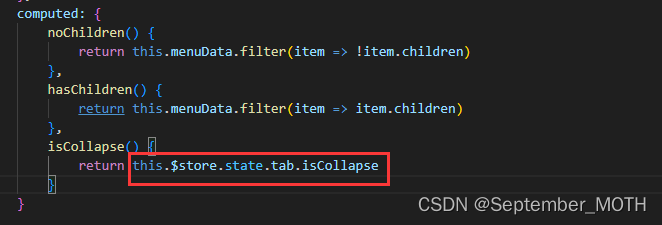
使用全局共享的数据