目录
- 1. Bagging
- 1.1 工作流程
- 1.2 代码实践
- 2. 随机森林
- 2.1 工作流程
- 2.2 代码实践
- 3. Adaboost
- 3.1 工作流程
- 3.2 样本权值的更新策略
- 3.3 代码实践
- 4. Stacking
- 4.1 代码实践
- 5. Voting
- 5.1 代码实践
- 6. 集成学习分类
1. Bagging
Bagging(bootstrap aggregating:自举汇聚法)也叫装袋法,其思想是通过将许多相互独立的学习器的结果进行结合,从而提高整体学习器的泛化能力,是一种并行集成学习方法。
1.1 工作流程
- 从原始样本集中使用Bootstraping(有放回抽样,这种抽样方法产生的样本子集能很好的反映总体的分布特性)方法抽取n个训练样本,共进行K轮抽取,得到K个训练集(训练集之间相互独立)。
- 对于每个训练集,使用相同的数据学习算法(比如决策树、KNN等)独立训练一个基本模型。
- 将测试样例输入到所有基本模型中,每个模型都给出一个预测值。对于分类问题:通过投票的方式确定分类结果(每个模型只有一票);对于回归问题:计算预测值的均值作为预测结果。
1.2 代码实践
from sklearn import neighbors
from sklearn import datasets
from sklearn.ensemble import BaggingClassifier
from sklearn import tree
from sklearn.model_selection import train_test_split
import numpy as np
import matplotlib.pyplot as plt#------------------------------------------------------------------#
# 使用datasets模块导入鸢尾花数据集,并切分特征值和标签值
# train_test_split(x_data, y_data):将数据集划分为测试集和训练集,
# 默认情况下,训练集占3/4,测试集占1/4
#-----------------------------------------------------------------#
iris = datasets.load_iris()
x_data = iris.data[:,:2]
y_data = iris.target
x_train, x_test, y_train, y_test = train_test_split(x_data, y_data)
# 利用等高线绘制分类边界图
def plot(model):# 获取数据值所在的范围x_min, x_max = x_data[:, 0].min() - 1, x_data[:, 0].max() + 1y_min, y_max = x_data[:, 1].min() - 1, x_data[:, 1].max() + 1# 生成网格矩阵元素xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),np.arange(y_min, y_max, 0.02))#-----------------------------------------------------## 预测分类结果# ravel():将多为数据展平为一维数据# np.c_:按列连接两个数组,即拼接成点的坐标的形式# contourf(xx, yy, z):创建填充等高线图,参数需为二维数组#-----------------------------------------------------#z = model.predict(np.c_[xx.ravel(), yy.ravel()])z = z.reshape(xx.shape)cs = plt.contourf(xx, yy, z)
# 创建KNN模型,使用训练集训练模型
knn = neighbors.KNeighborsClassifier()
knn.fit(x_train, y_train)
# 绘制分类边界图
plot(knn)
# 样本散点图
plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data)
# 打印准确率
knn.score(x_test, y_test)
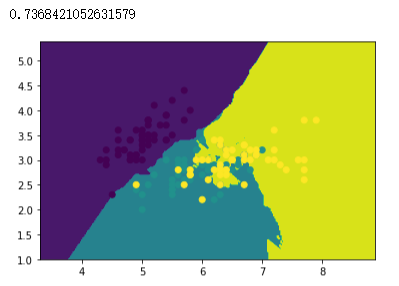
# 创建CART决策树模型,使用训练集训练模型
dtree = tree.DecisionTreeClassifier()
dtree.fit(x_train, y_train)
# 绘制分类边界图
plot(dtree)
# 样本散点图
plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data)
# 打印准确率
dtree.score(x_test, y_test)
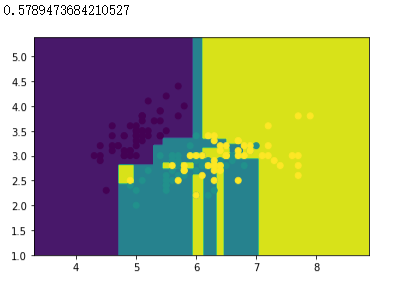
# 创建 Bagging 分类器对象,以KNN分类器作为基分类器,创建100个KNN基分类器
bagging_knn = BaggingClassifier(knn, n_estimators=100)
# 模型拟合
bagging_knn.fit(x_train, y_train)
# 绘制分类边界图
plot(bagging_knn)
# 样本散点图
plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data)
# 打印准确率
bagging_knn.score(x_test, y_test)
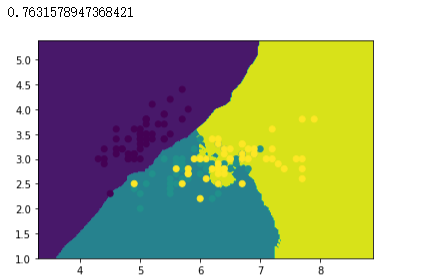
# 创建 Bagging 分类器对象,以CART决策树分类器作为基分类器,创建100个基分类器
bagging_tree = BaggingClassifier(dtree, n_estimators=100)
# 模型拟合
bagging_tree.fit(x_train, y_train)
# 绘制分类边界图
plot(bagging_tree)
# 样本散点图
plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data)
# 打印准确率
bagging_tree.score(x_test, y_test)
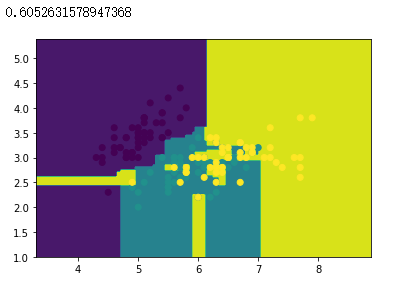
准确率汇总
| 算法 | 准确率 |
|---|---|
| KNN | 73.6 8% |
| Bagging(KNN) | 76.32% |
| DecisionTree | 57.89% |
| Bagging(DecisionTree) | 60.53% |
注:由于数据集切分的随机性和Bagging中每个基分类器所使用的训练集不同,因此每次运行的结果可能不同,且Bagging的准确率可能会比单分类器的准确率低。
2. 随机森林
随机森林(Random Forest)是通过集成学习的思想将多棵树(基分类器)进行集成的一种算法,它的基本单元是决策树。随机森林=决策树+Bagging+随机属性选择。
2.1 工作流程
- 样本随机选择:从原始样本集中使用Bootstraping(有放回抽样,这种抽样方法产生的样本子集能很好的反映总体的分布特性)方法抽取n个训练样本,共进行K轮抽取,得到K个训练集(训练集之间相互独立)。
- 特征随机选择:当决策树的每个节点需要分裂时,从所有属性 M 中随机选择 K 个属性 (K<<M,这样可以增加随机性,避免过拟合,并提高模型的多样性),然后从这 K 个属性中选择最佳分割属性作为节点的分裂属性,直到满足某个停止条件(例如达到最大深度、节点样本数小于阈值等)。
- 重复以上步骤 n 次,建立 n 棵 CART 决策树(决策树形成过程中没有进行剪枝),这 m 棵 CART 决策树形成随机森林。
- 通过投票的方式决定数据属于哪一类。
样本和特征的随机选择能很大程度上减少过拟合的风险(决策树容易过拟合),同时也能增强模型的准确性和泛化能力。
随机森林图示
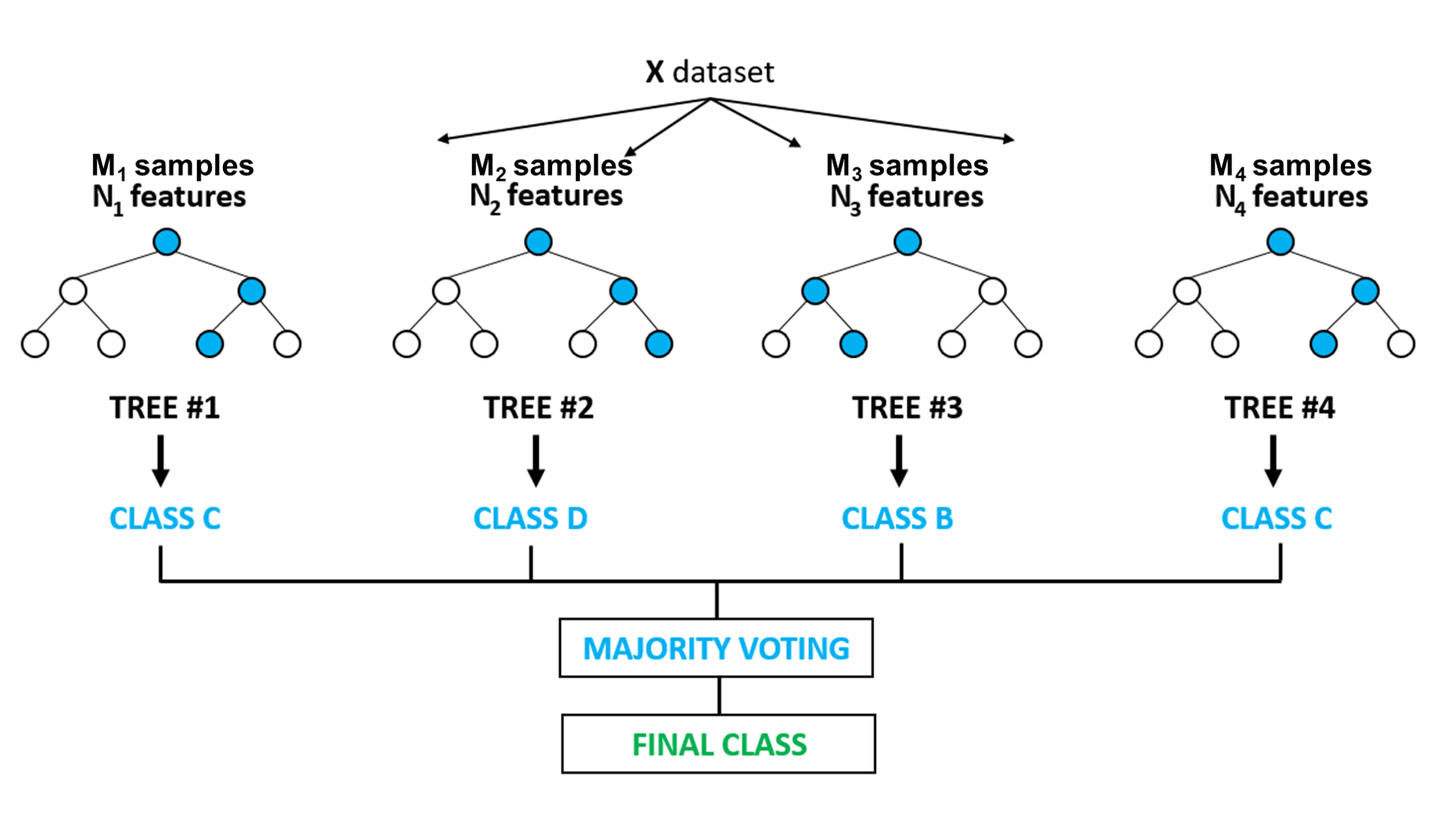
图中每棵树的样本集合和分支节点的特征均不相同。
2.2 代码实践
from sklearn import tree
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
import numpy as np
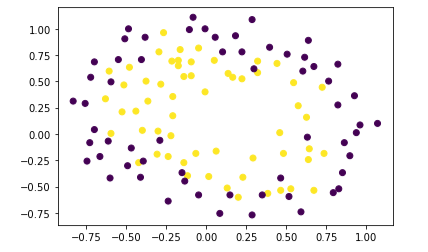
import matplotlib.pyplot as plt# 载入数据集,划分特征数据与标签数据,并绘制散点图
data = np.genfromtxt("LR-testSet2.txt", delimiter=",")
x_data = data[:,:-1]
y_data = data[:, -1]
plt.scatter(x_data[:,0],x_data[:,1],c=y_data)
# 将数据集切分为训练集和测试集,比例为1:1
x_train, x_test, y_train, y_test = train_test_split(x_data, y_data, test_size = 0.5)# 利用等高线绘制分类边界图
def plot(model):# 获取数据值所在的范围x_min, x_max = x_data[:, 0].min() - 1, x_data[:, 0].max() + 1y_min, y_max = x_data[:, 1].min() - 1, x_data[:, 1].max() + 1# 生成网格矩阵元素xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),np.arange(y_min, y_max, 0.02))#-----------------------------------------------------## 预测分类结果# ravel():将多为数据展平为一维数据# np.c_:按列连接两个数组,即拼接成点的坐标的形式# contourf(xx, yy, z):创建填充等高线图,参数需为二维数组#-----------------------------------------------------#z = model.predict(np.c_[xx.ravel(), yy.ravel()])z = z.reshape(xx.shape)cs = plt.contourf(xx, yy, z)
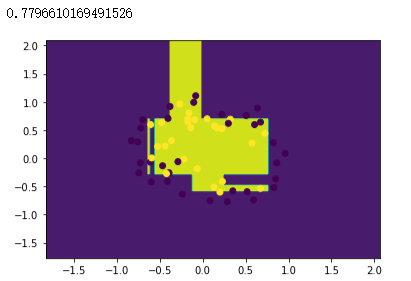
# 创建决策树模型,使用训练数据进行拟合
dtree = tree.DecisionTreeClassifier()
dtree.fit(x_train, y_train)# 绘制分类边界图和样本散点图
plot(dtree)
plt.scatter(x_test[:, 0], x_test[:, 1], c=y_test)
dtree.score(x_test, y_test)
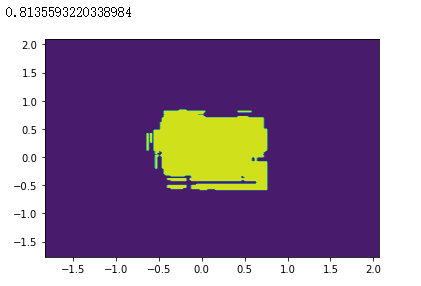
# 创建随机森林模型,其包含50个决策树基分类器
RF = RandomForestClassifier(n_estimators=50)
RF.fit(x_train, y_train)plot(RF)
RF.score(x_test, y_test)
3. Adaboost
AdaBoost(Adaptive Boosting:自适应增强)的自适应在于:前一个基分类器中被错误分类的样本的权值会增大(将学习器的重点放在容易出错的样本上可以提升学习器的性能),而正确分类的样本的权值会减小,并将样本用来训练下一个基分类器。同时,在每一轮迭代中,加入一个新的基分类器,直到达到某个预定的足够小的错误率或达到预先指定的最大迭代次数才确定最终的强分类器 ,Adaboost是一种串行集成学习方法,基学习器之间存在强依赖关系。
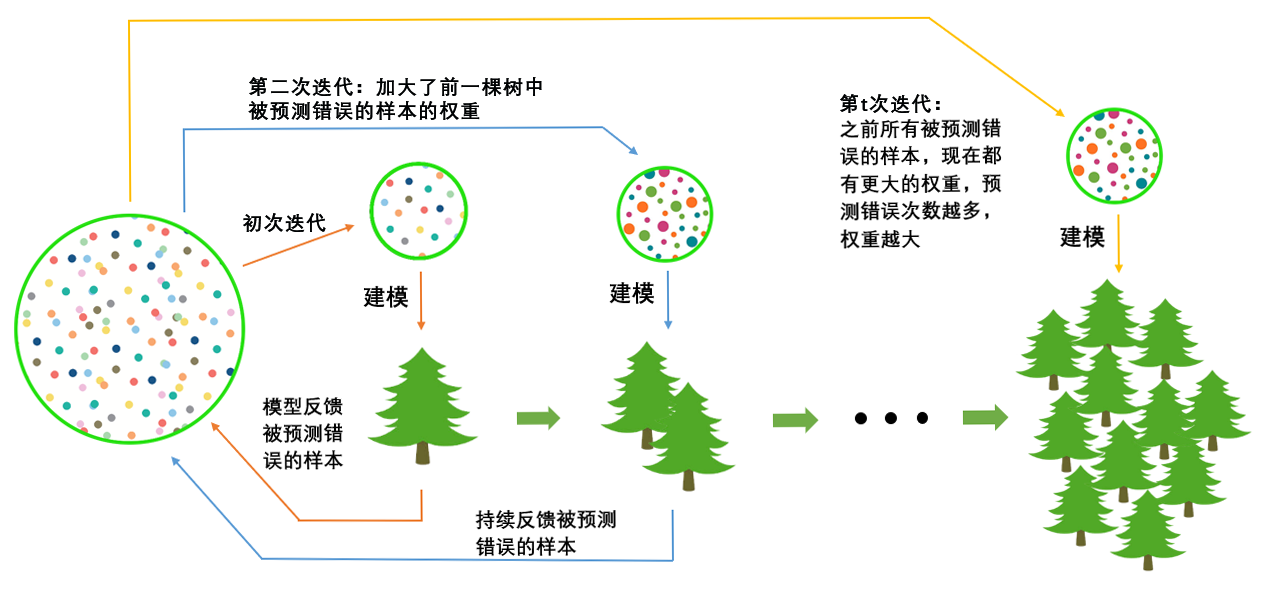
3.1 工作流程
- 初始化训练数据的权值分布,假设有 N 个训练样本,则每一个训练样本最开始时都被赋予相同的权值: w i = 1 N w_i =\frac{1}{N} wi=N1。
- 训练弱分类器 h i h_i hi,具体训练过程:如果某个训练样本被基分类器 h i h_i hi准确地分类,那么在构造下一个样本集时,它对应的权值要减小;相反,如果某个训练样本被错误分类,那么它的权值要增大。权值更新过的样本集被用于训练下一个基分类器,整个训练过程不断迭代。
- 将各个训练得到的弱分类器(基分类器)组合成一个强分类器。各个弱分类器的训练过程结束后,分类误差小的弱分类器的权重较大,使其在最终的分类函数中起着较大的决定作用,分类误差大的弱分类器的权重较小,使其在最终的分类函数中起着较小的决定作用。
3.2 样本权值的更新策略
对于第 t t t轮迭代,基分类器 h h h在训练集 D t D_t Dt上的错误率为 α t \alpha _t αt( α t < 0.5 \alpha _t<0.5 αt<0.5)。
则基分类器 h h h的权重更新公式
α t = 1 2 l n 1 − α t α t \alpha _t=\frac{1}{2}ln\frac{1-\alpha _t}{\alpha_t} αt=21lnαt1−αt
样本 i i i的权重更新公式
W i t + 1 = W i t e − α t Z t , y = y ^ W_i^{t+1}=\frac{W_i^{t}e^{-\alpha _t}}{Z_t},y=\hat{y} Wit+1=ZtWite−αt,y=y^
W i t + 1 = W i t e α t Z t , y ≠ y ^ W_i^{t+1}=\frac{W_i^{t}e^{\alpha _t}}{Z_t},y\ne\hat{y} Wit+1=ZtWiteαt,y=y^
其中, y y y为真实值, y ^ \hat{y} y^为预测值。样本被正确分类时,权重需减小;样本被错误分类时,权重需增大。 Z t Z_t Zt为归一化因子(更新后的样本权重之和),以保证样本权重之和为1。
样本 x x x最终的预测结果
H ( x ) = s i g m o i d ( ∑ t = 1 T α t h t ( x ) ) H(x)=sigmoid(\sum_{t=1}^T\alpha _th_t(x)) H(x)=sigmoid(t=1∑Tαtht(x))
3.3 代码实践
import numpy as np
import matplotlib.pyplot as plt
from sklearn import tree
from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import make_gaussian_quantiles
from sklearn.metrics import classification_report#-------------------------------------------------------------------------#
# make_gaussian_quantiles:生成具有高斯分布的量化数据
# n_samples:样本数量500个样本,2个样本特征,两个样本特征的均值默认为0
# n_features:每个样本的特征数
# n_classes:数据集的类别数
# mean:指定每个类别的均值
#-------------------------------------------------------------------------#
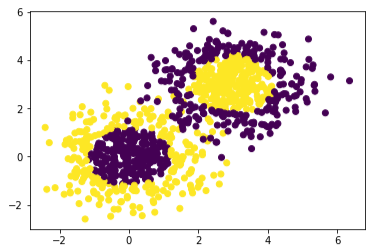
x1, y1 = make_gaussian_quantiles(n_samples=500, n_features=2, n_classes=2)
x2, y2 = make_gaussian_quantiles(mean=(3, 3), n_samples=500, n_features=2, n_classes=2)# 将两组数据合成一组数据
x_data = np.concatenate((x1, x2))
y_data = np.concatenate((y1, - y2 + 1))# 数据集散点图
plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data)
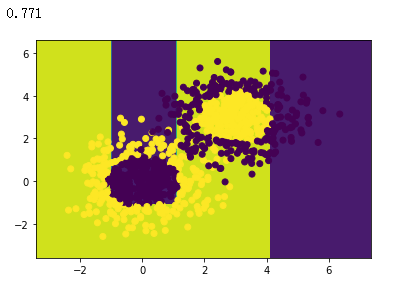
# 创建决策树模型并进行拟合
model = tree.DecisionTreeClassifier(max_depth=3)
model.fit(x_data, y_data)# 获取数据值所在的范围
x_min, x_max = x_data[:, 0].min() - 1, x_data[:, 0].max() + 1
y_min, y_max = x_data[:, 1].min() - 1, x_data[:, 1].max() + 1# 生成网格矩阵元素
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),np.arange(y_min, y_max, 0.02))#--------------------------------------------------------#
# 预测分类结果
# ravel():将多为数据展平为一维数据
# np.c_:按列连接两个数组,即拼接成点的坐标的形式
# contourf(xx, yy, z):创建填充等高线图,参数需为二维数组
#--------------------------------------------------------#
z = model.predict(np.c_[xx.ravel(), yy.ravel()])
z = z.reshape(xx.shape)
cs = plt.contourf(xx, yy, z)# 样本散点图
plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data)# 打印准确率
model.score(x_data,y_data)
# 创建AdaBoost模型,其包含10个基分类器
model = AdaBoostClassifier(DecisionTreeClassifier(max_depth=3), n_estimators=10)
# 训练模型
model.fit(x_data, y_data)# 获取数据值所在的范围
x_min, x_max = x_data[:, 0].min() - 1, x_data[:, 0].max() + 1
y_min, y_max = x_data[:, 1].min() - 1, x_data[:, 1].max() + 1# 生成网格矩阵元素
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),np.arange(y_min, y_max, 0.02))#--------------------------------------------------------#
# 预测分类结果
# ravel():将多为数据展平为一维数据
# np.c_:按列连接两个数组,即拼接成点的坐标的形式
# contourf(xx, yy, z):创建填充等高线图,参数需为二维数组
#--------------------------------------------------------#
z = model.predict(np.c_[xx.ravel(), yy.ravel()])
z = z.reshape(xx.shape)
cs = plt.contourf(xx, yy, z)# 样本散点图
plt.scatter(x_data[:, 0], x_data[:, 1], c=y_data)# 打印准确率
model.score(x_data,y_data)
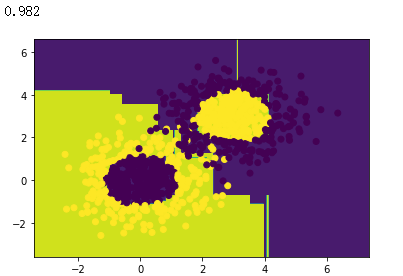
准确率从77.1%增加到98.2%,提升非常大。
4. Stacking
使用多个不同的分类器对训练集进预测,把预测得到的结果作为一个次级分类器的输入。次级分类器的输出是整个模型的预测结果。在Stacking方法中,有两个阶段的模型。 第一个阶段的模型是以原始训练集(无需抽样构造训练集,所有模型均使用相同的训练集)为输入的模型,叫做基模型(也叫 level-0 模型),可以选取多种基模型进行训练。第二个阶段的模型是以基模型在原始训练集上的预测作为训练集,以基模型在原始测试集上的预测作为测试集,叫做元模型(也叫 level-1 模型)1。
Stacking算法的结构图示如下
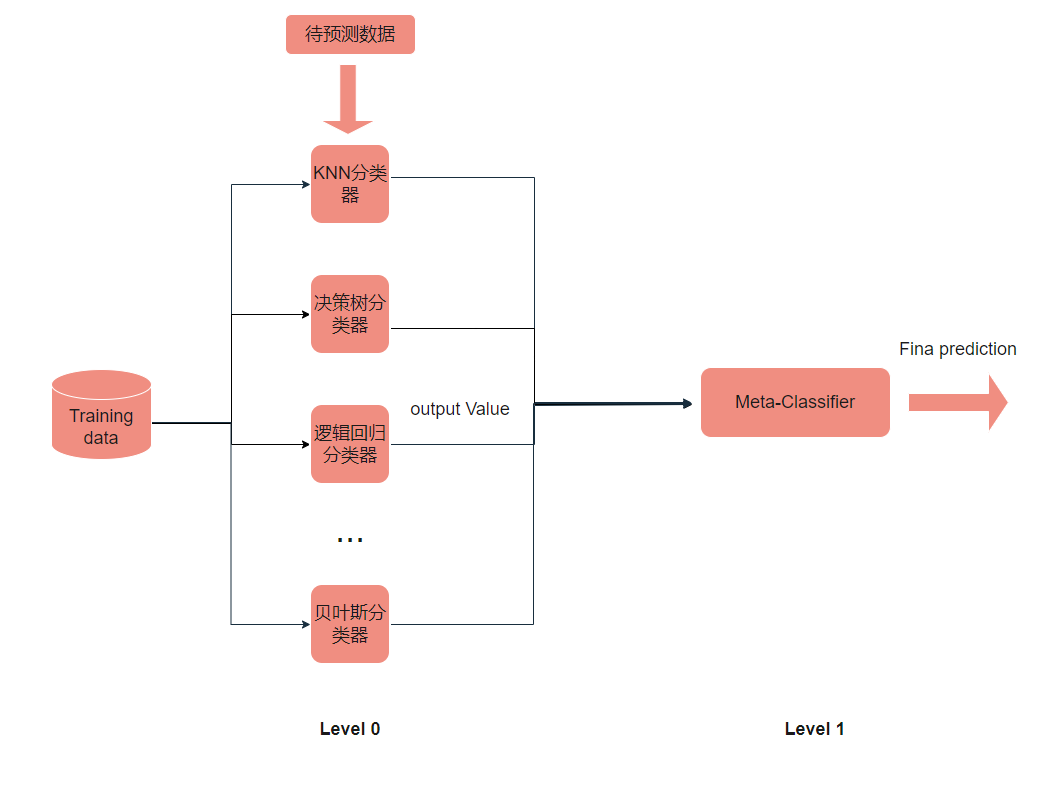
4.1 代码实践
from sklearn import datasets
from sklearn import model_selection
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
# 需安装mlxtend模块:pip install mlxtend
from mlxtend.classifier import StackingClassifier
import numpy as np # 载入数据集,只要第1,2列的特征
iris = datasets.load_iris()
x_data, y_data = iris.data[:, 1:3], iris.target # 定义三个不同的分类器
clf1 = KNeighborsClassifier(n_neighbors=1)
clf2 = DecisionTreeClassifier()
clf3 = LogisticRegression() # 定义一个次级分类器
lr = LogisticRegression()
sclf = StackingClassifier(classifiers=[clf1, clf2, clf3], meta_classifier=lr)# zip:用于将多个可迭代对象(例如列表、元组等)的对应元素打包成一个元组,返回一个迭代器
for clf,label in zip([clf1, clf2, clf3, sclf],['KNN','Decision Tree','LogisticRegression','StackingClassifier']): #------------------------------------------------------------------------------## 在实际使用Stacking方法时,为了避免过拟合的风险,常常伴随着交叉验证操作# 使用3折交叉验证,每次取其中的一份作为测试集,两份作为训练集# 3折交叉验证会输出3个准确率,这里取3个准确率的均值# cross_val_score:计算交叉验证的评分#------------------------------------------------------------------------------#scores = model_selection.cross_val_score(clf, x_data, y_data, cv=3, scoring='accuracy') print("Accuracy: %0.2f [%s]" % (scores.mean(), label))
运行结果
Accuracy: 0.91 [KNN]
Accuracy: 0.93 [Decision Tree]
Accuracy: 0.95 [LogisticRegression]
Accuracy: 0.93 [StackingClassifier]
5. Voting
对基分类器的预测结果使用投票的方式确定最终预测结果。
5.1 代码实践
from sklearn import datasets
from sklearn import model_selection
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import VotingClassifier
from sklearn.model_selection import train_test_split
import numpy as np# 载入数据集,只要第1,2列的特征(使单个分类器与Voting分类器的准确率之间存在差距,便于观察Voting分类器在准确率上的提升)。
iris = datasets.load_iris()
x_data, y_data = iris.data[:, 1:3], iris.target # 定义三个不同的分类器
clf1 = KNeighborsClassifier(n_neighbors=1)
clf2 = DecisionTreeClassifier()
clf3 = LogisticRegression() # 定义Voting分类器
sclf = VotingClassifier([('knn',clf1),('dtree',clf2), ('lr',clf3)]) # zip:用于将多个可迭代对象(例如列表、元组等)的对应元素打包成一个元组,返回一个迭代器
for clf, label in zip([clf1, clf2, clf3, sclf],['KNN','Decision Tree','LogisticRegression','VotingClassifier']): #------------------------------------------------------------------------------## 为了避免过拟合的风险,使用交叉验证方法# 使用3折交叉验证,每次取其中的一份作为测试集,两份作为训练集# 3折交叉验证会输出3个准确率,这里取3个准确率的均值# cross_val_score:计算交叉验证的评分#------------------------------------------------------------------------------#scores = model_selection.cross_val_score(clf, x_data, y_data, cv=3, scoring='accuracy') print("Accuracy: %0.2f [%s]" % (scores.mean(), label))
运行结果
Accuracy: 0.91 [KNN]
Accuracy: 0.91 [Decision Tree]
Accuracy: 0.95 [LogisticRegression]
Accuracy: 0.95 [VotingClassifier]
# 将数据集划分为训练集和测试集
xtrain, xtest, ytrain, ytest = train_test_split(x_data, y_data, test_size=0.2)# 定义并训练三个不同的分类器
clf1 = KNeighborsClassifier(n_neighbors=1)
clf1.fit(xtrain, ytrain)
clf2 = DecisionTreeClassifier()
clf2.fit(xtrain, ytrain)
clf3 = LogisticRegression()
clf3.fit(xtrain, ytrain)# 定义并训练Voting分类器
sclf = VotingClassifier([('knn',clf1),('dtree',clf2), ('lr',clf3)])
sclf.fit(xtrain, ytrain)# 实际预测
print("KNN:{}".format(clf1.score(xtest,ytest)))
print("DecisionTree:{}".format(clf2.score(xtest,ytest)))
print("Logistic:{}".format(clf3.score(xtest,ytest)))
print("Voting:{}".format(sclf.score(xtest,ytest)))
运行结果
KNN:0.9
DecisionTree:0.9666666666666667
Logistic:0.9333333333333333
Voting:0.9666666666666667
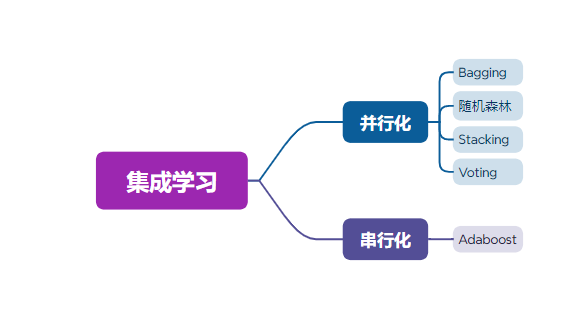
6. 集成学习分类
按照基分类器的生成方式可分为
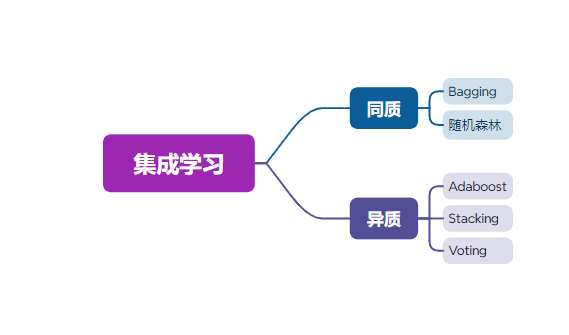
按照是否使用同一种基学习器(使用同一种基学习器的方法称为同质集成方法)可分为
集成学习之Stacking(堆栈)方法 ↩︎




:应用层(待更新))

)




)







—— Flume 自定义组件)