文章目录
- 09 后端 2
- 9.1 滑动窗口滤波和优化
- 9.1.1 实际环境下的 BA 结构
- 9.1.2 滑动窗口法
- 9.2 位姿图
- 9.2.1 位姿图的意义
- 9.2.2 位姿图优化
09 后端 2
9.1 滑动窗口滤波和优化
9.1.1 实际环境下的 BA 结构
由于计算机算力的限制,我们必须控制 BA 的规模,一种简单的思路是仅保留离当前时刻最近的 N N N 个关键帧,去掉时间上更早的关键帧。于是,BA 被固定在一个时间窗口内,离开这个窗口的即被抛弃,称为 滑动窗口法。
或者像 ORB-SLAM 2 那样,定义一种称为 共视图 的结构,即与当前相机存在共同观测的关键帧构成的图。在 BA 优化时,按照某些原则在共视图内取一些关键帧和路标进行优化。
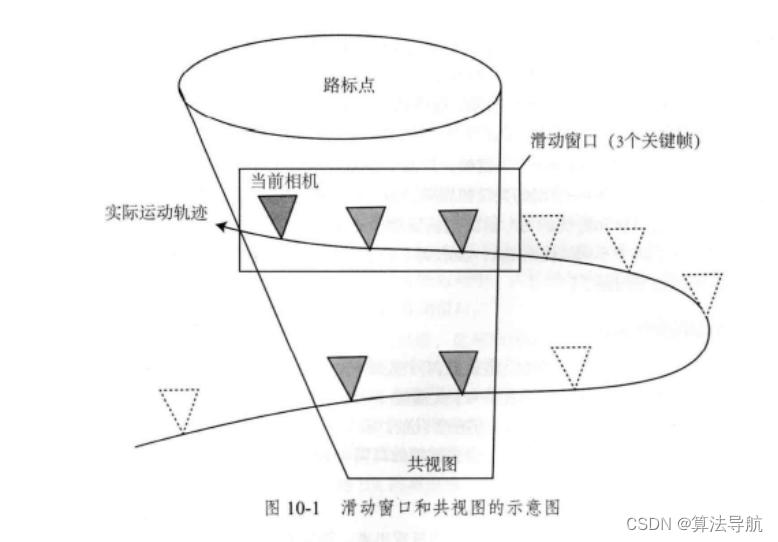
9.1.2 滑动窗口法
(1)现在考虑一个滑动窗口,假设窗口内有 N N N 个关键帧,他们的位姿表达为(李代数形式):
x 1 , x 2 , . . . , x N \boldsymbol{x}_1, \boldsymbol{x}_2,...,\boldsymbol{x}_N x1,x2,...,xN
假设这个滑动窗口中还有 M M M 个路标点 y 1 , y 2 , . . . , y M \boldsymbol{y}_1, \boldsymbol{y}_2,...,\boldsymbol{y}_M y1,y2,...,yM,用上一讲中的 BA 方法来处理这个滑动窗口,包括建立图优化模型,构建海森矩阵,在边缘化所有路标点来加速求解。边缘化时,考虑关键帧的位姿:
[ x 1 , … , x N ] T ∼ N ( [ μ 1 , … , μ N ] T , Σ ) (9-1) \left[\boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{N}\right]^{\mathrm{T}} \sim N\left(\left[\boldsymbol{\mu}_{1}, \ldots, \boldsymbol{\mu}_{N}\right]^{\mathrm{T}}, \boldsymbol{\Sigma}\right) \tag{9-1} [x1,…,xN]T∼N([μ1,…,μN]T,Σ)(9-1)
其中 μ k \boldsymbol{\mu}_k μk 为第 k k k 个关键帧的位姿均值, Σ \boldsymbol{\Sigma} Σ 为所有关键帧的协方差矩阵。显然,均值部分就是 BA 迭代之后的结果, Σ \boldsymbol{\Sigma} Σ 是对整个 BA 的 H \boldsymbol{H} H 矩阵进行边缘化之后的结果。
(2)当窗口结构改变时:
① 先在窗口中新增一个关键帧,以及观测到的路标点;
② 把窗口中一个旧的关键帧删除,可能会删除他观测到的路标点。
- 新增一个关键帧和路标点
将新的关键帧 x N + 1 \boldsymbol{x}_{N+1} xN+1 按照正常的 BA 流程处理即可。
- 删除一个旧的关键帧
删除旧的关键帧时,就比较麻烦。比如删除 x 1 \boldsymbol{x}_1 x1 ,但 x 1 \boldsymbol{x}_1 x1 并不是孤立的,它会和其它帧观测到同样的路标,将 x 1 \boldsymbol{x}_1 x1 边缘化后将导致整个问题不再稀疏(破坏了路标部分的对角块结构)。
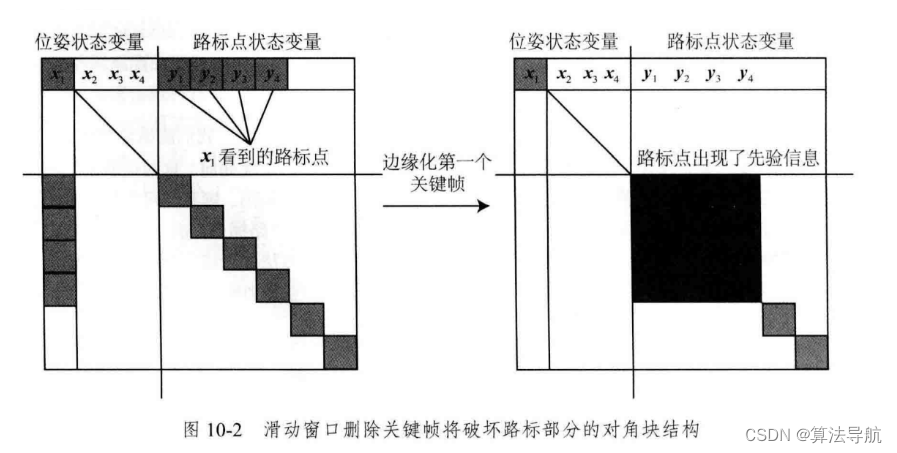
(3)滑动窗口法适合 VO 系统,而不适合大规模建图的系统。
9.2 位姿图
9.2.1 位姿图的意义
(1)随着时间的流逝,机器人的运动轨迹会越来越长,地图规模也会越来越大,BA 的计算效率就会下降。同时我们发现,经过若干次迭代后,收敛的特征点位置变化很小,发散的外点则已被剔除,因此在后续优化中没有必要再将收敛点考虑进来,而是只把他们当做位姿估计的约束。
(2)放开思路,我们完全可以构建一个只有轨迹的图优化,而位姿节点的边,可以由两个关键帧之间通过特征匹配之后得到的运动估计来给定初始值。一旦初始估计完成,就不再优化那些路标点的位置,而只关心相机位姿之间的联系。这样的方式,省去了大量特征点优化的计算,只保留了关键帧的轨迹,构建了所谓的 位姿图。
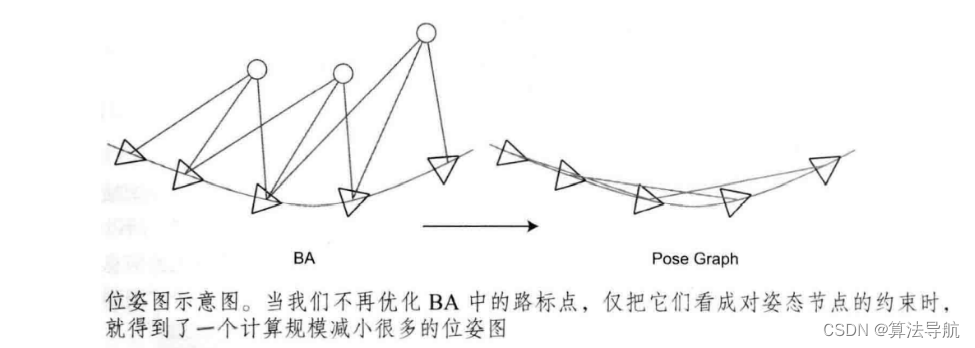
通过舍弃对路标点的优化,提高计算效率。
9.2.2 位姿图优化
位姿图中的节点表示相机位姿,用 T 1 , T 2 , . . . , T n , \boldsymbol{T}_1,\boldsymbol{T}_2,...,\boldsymbol{T}_n, T1,T2,...,Tn, 表示,边则是两个位姿节点之间相对运动的估计,这个估计可以通过特征点法或直接法得到。假设我们估计了 T i \boldsymbol{T}_i Ti 和 T j \boldsymbol{T}_j Tj 之间的相对运动 T i j \boldsymbol{T}_{ij} Tij,则有
T i T i j = T j \boldsymbol{T}_i \boldsymbol{T}_{ij}=\boldsymbol{T}_j TiTij=Tj
也即
T i j = T i − 1 T j (9-2) \boldsymbol{T}_{ij}=\boldsymbol{T}_i^{-1}\boldsymbol{T}_j \tag{9-2} Tij=Ti−1Tj(9-2)
写成李代数形式
ξ i j = ξ i − 1 ∘ ξ j = ln ( T i − 1 T j ) ∨ (9-3) \boldsymbol{\xi}_{i j}=\boldsymbol{\xi}_{i}^{-1} \circ \boldsymbol{\xi}_{j}=\ln \left(\boldsymbol{T}_{i}^{-1} \boldsymbol{T}_{j}\right)^{\vee} \tag{9-3} ξij=ξi−1∘ξj=ln(Ti−1Tj)∨(9-3)
将式(9-2)中的 Δ T i j \Delta \boldsymbol{T}_{ij} ΔTij 移至方程右侧,则
T i j − 1 T i − 1 T j = I (9-4) \boldsymbol{T}_{ij}^{-1}\boldsymbol{T}_i^{-1}\boldsymbol{T}_j=\boldsymbol{I} \tag{9-4} Tij−1Ti−1Tj=I(9-4)
但实际上,并不可能完全相等。定义
e i j = ln ( T i j − 1 T i − 1 T j ) ∨ (9-5) \boldsymbol{e}_{ij}=\ln( \boldsymbol{T}_{ij}^{-1}\boldsymbol{T}_i^{-1}\boldsymbol{T}_j)^{\vee} \tag{9-5} eij=ln(Tij−1Ti−1Tj)∨(9-5)
我们需要优化的是 T i \boldsymbol{T}_i Ti 和 T j \boldsymbol{T}_j Tj,也即 ξ i \boldsymbol{\xi}_i ξi 和 ξ j \boldsymbol{\xi}_j ξj,因此需要求这两个变量关于 e i j \boldsymbol{e}_{ij} eij 的导数。分别左乘一个左扰动: δ ξ i \boldsymbol{\delta \xi}_i δξi 和 δ ξ j \boldsymbol{\delta \xi}_j δξj
e ^ i j = ln ( T i j − 1 T i − 1 exp ( ( − δ ξ i ) ∧ exp ( ( δ ξ j ) ∧ T j ) ∨ (9-6) \boldsymbol{\hat{e}}_{ij}=\ln( \boldsymbol{T}_{ij}^{-1}\boldsymbol{T}_i^{-1} \exp((-\boldsymbol{\delta \xi}_i)^{\wedge}\exp((\boldsymbol{\delta \xi}_j)^{\wedge} \boldsymbol{T}_j)^{\vee} \tag{9-6} e^ij=ln(Tij−1Ti−1exp((−δξi)∧exp((δξj)∧Tj)∨(9-6)
根据伴随矩阵的性质:
exp ( ( Ad ( T ) ξ ) ∧ ) = T exp ( ξ ∧ ) T − 1 (9-7) \exp \left((\operatorname{Ad}(\boldsymbol{T}) \boldsymbol{\xi})^{\wedge}\right)=\boldsymbol{T} \exp \left(\boldsymbol{\xi}^{\wedge}\right) \boldsymbol{T}^{-1} \tag{9-7} exp((Ad(T)ξ)∧)=Texp(ξ∧)T−1(9-7)
稍作改变(把 Ad ( T ) \operatorname{Ad}(\boldsymbol{T}) Ad(T) 移到右侧,$ \boldsymbol{T}^{-1}$ 移到左侧)
exp ( ξ ∧ ) T = T exp ( ( Ad ( T − 1 ) ξ ) ∧ ) (9-9) \exp \left(\boldsymbol{\xi}^{\wedge}\right) \boldsymbol{T}=\boldsymbol{T} \exp \left(\left(\operatorname{Ad}\left(\boldsymbol{T}^{-1}\right) \boldsymbol{\xi}\right)^{\wedge}\right) \tag{9-9} exp(ξ∧)T=Texp((Ad(T−1)ξ)∧)(9-9)
那么,式(9-6)可写为(从右往左化简)
e ^ i j = ln ( T i j − 1 T i − 1 exp ( ( − δ ξ i ) ∧ ) exp ( δ ξ j ∧ ) T j ‾ ) ∨ = ln ( T i j − 1 T i − 1 exp ( ( − δ ξ i ) ∧ ) T j ‾ exp ( ( Ad ( T j − 1 ) δ ξ j ) ∧ ) ) ∨ = ln ( T i j − 1 T i − 1 T j exp ( ( − Ad ( T j − 1 ) δ ξ i ) ∧ ) exp ( ( Ad ( T j − 1 ) δ ξ j ) ∧ ) ) ∨ ≈ ln ( T i j − 1 T i − 1 T j [ I − ( Ad ( T j − 1 ) δ ξ i ) ∧ + ( Ad ( T j − 1 ) δ ξ j ) ∧ ] ) ∨ ≈ e i j + ∂ e i j ∂ δ ξ i δ ξ i + ∂ e i j ∂ δ ξ j δ ξ j (9-10) \begin{aligned} \hat{\boldsymbol{e}}_{i j} &=\ln \left(\boldsymbol{T}_{i j}^{-1} \boldsymbol{T}_{i}^{-1} \exp \left(\left(-\boldsymbol{\delta} \boldsymbol{\xi}_{i}\right)^{\wedge}\right) \underline{\exp \left(\delta \boldsymbol{\xi}_{j}^{\wedge}\right) \boldsymbol{T}_{j}}\right)^{\vee} \\ &=\ln \left(\boldsymbol{T}_{i j}^{-1} \boldsymbol{T}_{i}^{-1} \underline{\exp \left(\left(-\boldsymbol{\delta} \boldsymbol{\xi}_{i}\right)^{\wedge}\right) \boldsymbol{T}_{j}} \exp \left(\left(\operatorname{Ad}\left(\boldsymbol{T}_{j}^{-1}\right) \boldsymbol{\delta} \boldsymbol{\xi}_{j}\right)^{\wedge}\right)\right)^{\vee} \\ &=\ln \left(\boldsymbol{T}_{i j}^{-1} \boldsymbol{T}_{i}^{-1} \boldsymbol{T}_{j} \exp \left(\left(-\operatorname{Ad}\left(\boldsymbol{T}_{j}^{-1}\right) \boldsymbol{\delta} \boldsymbol{\xi}_{i}\right)^{\wedge}\right) \exp \left(\left(\operatorname{Ad}\left(\boldsymbol{T}_{j}^{-1}\right) \boldsymbol{\delta} \boldsymbol{\xi}_{j}\right)^{\wedge}\right)\right)^{\vee} \\ & \approx \ln \left(\boldsymbol{T}_{i j}^{-1} \boldsymbol{T}_{i}^{-1} \boldsymbol{T}_{j}\left[\boldsymbol{I}-\left(\operatorname{Ad}\left(\boldsymbol{T}_{j}^{-1}\right) \boldsymbol{\delta} \boldsymbol{\xi}_{i}\right)^{\wedge}+\left(\operatorname{Ad}\left(\boldsymbol{T}_{j}^{-1}\right) \boldsymbol{\delta} \boldsymbol{\xi}_{j}\right)^{\wedge}\right]\right)^{\vee} \\ & \approx \boldsymbol{e}_{i j}+\frac{\partial \boldsymbol{e}_{i j}}{\partial \boldsymbol{\delta} \boldsymbol{\xi}_{i}} \boldsymbol{\delta} \boldsymbol{\xi}_{i}+\frac{\partial \boldsymbol{e}_{i j}}{\partial \boldsymbol{\delta} \boldsymbol{\xi}_{j}} \boldsymbol{\delta} \boldsymbol{\xi}_{j} \end{aligned} \tag{9-10} e^ij=ln(Tij−1Ti−1exp((−δξi)∧)exp(δξj∧)Tj)∨=ln(Tij−1Ti−1exp((−δξi)∧)Tjexp((Ad(Tj−1)δξj)∧))∨=ln(Tij−1Ti−1Tjexp((−Ad(Tj−1)δξi)∧)exp((Ad(Tj−1)δξj)∧))∨≈ln(Tij−1Ti−1Tj[I−(Ad(Tj−1)δξi)∧+(Ad(Tj−1)δξj)∧])∨≈eij+∂δξi∂eijδξi+∂δξj∂eijδξj(9-10)
其中,第四步将两个指数一阶泰勒展开,相乘后舍去二次项;第四步到第五步则使用了 BCH 近似。
按照李代数上的求导法则,我们得到了误差关于两个位姿的雅克比矩阵,即
∂ e i j ∂ δ ξ i = − J r − 1 ( e i j ) Ad ( T j − 1 ) \frac{\partial \boldsymbol{e}_{i j}}{\partial \boldsymbol{\delta} \boldsymbol{\xi}_{i}}=-\mathcal{J}_{r}^{-1}\left(\boldsymbol{e}_{i j}\right) \operatorname{Ad}\left(\boldsymbol{T}_{j}^{-1}\right) ∂δξi∂eij=−Jr−1(eij)Ad(Tj−1)
∂ e i j ∂ δ ξ j = J r − 1 ( e i j ) Ad ( T j − 1 ) (9-11) \frac{\partial \boldsymbol{e}_{i j}}{\partial \boldsymbol{\delta} \boldsymbol{\xi}_{j}}=\mathcal{J}_{r}^{-1}\left(\boldsymbol{e}_{i j}\right) \operatorname{Ad}\left(\boldsymbol{T}_{j}^{-1}\right) \tag{9-11} ∂δξj∂eij=Jr−1(eij)Ad(Tj−1)(9-11)
J r \mathcal{J}_{r} Jr 的形式比较复杂,通常取它的近似,
J r − 1 ( e i j ) ≈ I + 1 2 [ ϕ e ∧ ρ e ∧ 0 ϕ e ∧ ] (9-12) \mathcal{J}_{r}^{-1}\left(e_{i j}\right) \approx \boldsymbol{I}+\frac{1}{2}\left[\begin{array}{cc} \phi_{e}^{\wedge} & \rho_{e}^{\wedge} \\ 0 & \phi_{e}^{\wedge} \end{array}\right] \tag{9-12} Jr−1(eij)≈I+21[ϕe∧0ρe∧ϕe∧](9-12)
了解雅克比求导后,剩下的部分就是普通的图优化。 记所有的边(也就是位姿)为 E \mathcal{E} E,则总体目标函数为
min 1 2 ∑ i , j ∈ E e i j T Σ i j − 1 e i j (9-13) \min \frac{1}{2} \sum_{i, j \in \mathcal{E}} \boldsymbol{e}_{i j}^{\mathrm{T}} \boldsymbol{\Sigma}_{i j}^{-1} \boldsymbol{e}_{i j} \tag{9-13} min21i,j∈E∑eijTΣij−1eij(9-13)
然后再用高斯牛顿法或 L-M 法优化求解。








)










环形链表)