传递函数的推导和理解
假设有一个线性系统,在一般情况下,它的激励 x ( t ) x(t) x(t)与响应 y ( t ) y(t) y(t)所满足的的关系,可用下列微分方程来表示:
a n y ( n ) + a n − 1 y ( n − 1 ) + a n − 2 y ( n − 2 ) + ⋯ + a 1 y ′ + a 0 y = b m x ( m ) + b m − 1 x ( m − 1 ) + b m − 2 x ( m − 2 ) + ⋯ + b 1 x ′ + b 0 x (1) \begin{array}{l}{a_n}{y^{(n)}} + {a_{n - 1}}{y^{(n - 1)}} + {a_{n - 2}}{y^{(n - 2)}} + \cdots + {a_1}y' + {a_0}y\\ = {b_m}{x^{({\rm{m}})}} + {b_{m - 1}}{x^{({\rm{m - 1}})}} + {b_{m - 2}}{x^{({\rm{m - 2}})}} + \cdots + {b_1}x' + {b_0}x\end{array}\tag1 any(n)+an−1y(n−1)+an−2y(n−2)+⋯+a1y′+a0y=bmx(m)+bm−1x(m−1)+bm−2x(m−2)+⋯+b1x′+b0x(1)
其中, a 0 , a 1 , ⋯ , a n , b 0 , b 1 , ⋯ , b m {a_0},{a_1}, \cdots ,{a_n},{b_0},{b_1}, \cdots ,{b_m} a0,a1,⋯,an,b0,b1,⋯,bm均为常数, m , n m,n m,n为正整数, n ≥ m n \ge m n≥m
设 L [ y ( t ) ] = Y ( s ) , L [ x ( t ) ] = X ( s ) \mathscr{L}[y(t)]=Y(s),\mathscr{L}[x(t)]=X(s) L[y(t)]=Y(s),L[x(t)]=X(s),根据Laplace变换的微分性质,有
L [ a k y ( k ) ] = a k s k Y ( s ) − a k [ s k − 1 y ( 0 ) + s k − 2 y ′ ( 0 ) + s k − 3 y ′ ′ ( 0 ) + ⋯ + s k − ( k − 1 ) y ( k − 2 ) ( 0 ) + s 0 y ( k − 1 ) ( 0 ) ] ( k = 0 , 1 , 2 , ⋯ , n ) {\mathscr L}[{a_k}{y^{(k)}}] = {a_k}{s^k}Y(s) - {a_k}[{s^{k - 1}}y(0) + {s^{k - 2}}y'(0) + {s^{k - 3}}y''(0) + \cdots + {s^{k - (k - 1)}}{y^{(k - 2)}}(0) + {s^0}{y^{(k - 1)}}(0)]\\(k = 0,1,2, \cdots ,n) L[aky(k)]=akskY(s)−ak[sk−1y(0)+sk−2y′(0)+sk−3y′′(0)+⋯+sk−(k−1)y(k−2)(0)+s0y(k−1)(0)](k=0,1,2,⋯,n)
L [ b k x ( k ) ] = b k s k X ( s ) − b k [ s k − 1 x ( 0 ) + s k − 2 x ′ ( 0 ) + s k − 3 x ′ ′ ( 0 ) + ⋯ + s k − ( k − 1 ) x ( k − 2 ) ( 0 ) + s 0 x ( k − 1 ) ( 0 ) ] ( k = 0 , 1 , 2 , ⋯ , m ) {\mathscr L}[{b_k}{x^{(k)}}] = {b_k}{s^k}X(s) - {b_k}[{s^{k - 1}}x(0) + {s^{k - 2}}x'(0) + {s^{k - 3}}x''(0) + \cdots + {s^{k - (k - 1)}}{x^{(k - 2)}}(0) + {s^0}{x^{(k - 1)}}(0)] \\(k = 0,1,2, \cdots ,m) L[bkx(k)]=bkskX(s)−bk[sk−1x(0)+sk−2x′(0)+sk−3x′′(0)+⋯+sk−(k−1)x(k−2)(0)+s0x(k−1)(0)](k=0,1,2,⋯,m)
对式子(1)两边进行Laplace变换并通过整理,可得:
D ( s ) Y ( s ) − M h y ( s ) = M ( s ) X ( s ) − M h x ( s ) D(s)Y(s) - {M_{hy}}(s) = M(s)X(s) - {M_{hx}}(s) D(s)Y(s)−Mhy(s)=M(s)X(s)−Mhx(s)
即:
Y ( s ) = M ( s ) D ( s ) X ( s ) + M h y ( s ) − M h x ( s ) D ( s ) (2) Y(s) = \frac{{M(s)}}{{D(s)}}X(s) + \frac{{{M_{hy}}(s) - {M_{hx}}(s)}}{{D(s)}}\tag2 Y(s)=D(s)M(s)X(s)+D(s)Mhy(s)−Mhx(s)(2)
其中,
D ( s ) = a n s n + a n − 1 s n − 1 + ⋯ + a 1 s + a 0 , D(s) = {a_n}{s^n} + {a_{n - 1}}{s^{n - 1}} + \cdots + {a_1}s + {a_0}, D(s)=ansn+an−1sn−1+⋯+a1s+a0,
M ( s ) = b m s m + b m − 1 s m − 1 + ⋯ + b 1 s + b 0 , M(s) = {b_m}{s^m} + {b_{m - 1}}{s^{m - 1}} + \cdots + {b_1}s + {b_0}, M(s)=bmsm+bm−1sm−1+⋯+b1s+b0,
M h y ( s ) = a n y ( 0 ) s n − 1 + [ a n y ′ ( 0 ) + a n − 1 y ( 0 ) ] s n − 2 + [ a n y ′ ′ ( 0 ) + a n − 1 y ′ ( 0 ) + a n − 2 y ( 0 ) ] s n − 3 + ⋯ + [ a n y ( n − 2 ) ( 0 ) + a n − 1 y ( n − 3 ) ( 0 ) + ⋯ + a 2 y ( 0 ) ] s + [ a n y ( n − 1 ) ( 0 ) + a n − 1 y ( n − 2 ) ( 0 ) + ⋯ + a 1 y ( 0 ) ] , {M_{hy}}(s) = {a_n}y(0){s^{n - 1}} + [{a_n}y'(0) + {a_{n - 1}}y(0)]{s^{n - 2}} + [{a_n}y''(0) + {a_{n - 1}}y'(0) + {a_{n - 2}}y(0)]{s^{n - 3}} + \cdots + [{a_n}{y^{(n - 2)}}(0) + {a_{n - 1}}{y^{(n - 3)}}(0) + \cdots + {a_2}y(0)]s + [{a_n}{y^{(n - 1)}}(0) + {a_{n - 1}}{y^{(n - 2)}}(0) + \cdots + {a_1}y(0)], Mhy(s)=any(0)sn−1+[any′(0)+an−1y(0)]sn−2+[any′′(0)+an−1y′(0)+an−2y(0)]sn−3+⋯+[any(n−2)(0)+an−1y(n−3)(0)+⋯+a2y(0)]s+[any(n−1)(0)+an−1y(n−2)(0)+⋯+a1y(0)],
M h x ( s ) = b m x ( 0 ) s m − 1 + [ b m x ′ ( 0 ) + b m − 1 x ( 0 ) ] s m − 2 + [ b m x ′ ′ ( 0 ) + b m − 1 x ′ ( 0 ) + b m − 2 x ( 0 ) ] s m − 3 + ⋯ + [ b m x ( m − 2 ) ( 0 ) + b m − 1 x ( m − 3 ) ( 0 ) + ⋯ + b 2 x ( 0 ) ] s + [ b m x ( m − 1 ) ( 0 ) + b m − 1 x ( n − 2 ) ( 0 ) + ⋯ + b 1 x ( 0 ) ] , {M_{hx}}(s) = {b_m}x(0){s^{m - 1}} + [{b_m}x'(0) + {b_{m - 1}}x(0)]{s^{m - 2}} + [{b_m}x''(0) + {b_{m - 1}}x'(0) + {b_{m - 2}}x(0)]{s^{m - 3}} + \cdots + [{b_m}{x^{(m - 2)}}(0) + {b_{m - 1}}{x^{(m - 3)}}(0) + \cdots + {b_2}x(0)]s + [{b_m}{x^{(m - 1)}}(0) + {b_{m - 1}}{x^{(n - 2)}}(0) + \cdots + {b_1}x(0)], Mhx(s)=bmx(0)sm−1+[bmx′(0)+bm−1x(0)]sm−2+[bmx′′(0)+bm−1x′(0)+bm−2x(0)]sm−3+⋯+[bmx(m−2)(0)+bm−1x(m−3)(0)+⋯+b2x(0)]s+[bmx(m−1)(0)+bm−1x(n−2)(0)+⋯+b1x(0)],
若令 G ( s ) = M ( s ) G ( s ) G(s) = \frac{{M(s)}}{{G(s)}} G(s)=G(s)M(s), G h ( s ) = M h y ( s ) − M h x ( s ) D ( s ) {G_h}(s) = \frac{{{M_{hy}}(s) - {M_{hx}}(s)}}{{D(s)}} Gh(s)=D(s)Mhy(s)−Mhx(s),则式(2)可写为:
Y ( s ) = G ( s ) X ( s ) + G h ( s ) (3) Y(s) = G(s)X(s) + {G_h}(s)\tag3 Y(s)=G(s)X(s)+Gh(s)(3)
式子中:
G ( s ) = b m s m + b m − 1 s m − 1 + ⋯ + b 1 s + b 0 a n s n + a n − 1 s n − 1 + ⋯ + a 1 s + a 0 (4) G(s) = \frac{{{b_m}{s^m} + {b_{m - 1}}{s^{m - 1}} + \cdots + {b_1}s + {b_0}}}{{{a_n}{s^n} + {a_{n - 1}}{s^{n - 1}} + \cdots + {a_1}s + {a_0}}}\tag4 G(s)=ansn+an−1sn−1+⋯+a1s+a0bmsm+bm−1sm−1+⋯+b1s+b0(4)
我们称 G ( s ) G(s) G(s)为系统的传递函数。它表达了系统本身的特性,而与激励及系统的初始状态无关。
但是 G h ( s ) G_{h}(s) Gh(s)则由激励和系统本身的初值条件所决定。若这些初始条件全为0,即 G h ( s ) G_{h}(s) Gh(s)=0时,式子(3)可写成:
Y ( s ) = G ( s ) X ( s ) 或 G ( s ) = Y ( s ) X ( s ) (5) \begin{array}{l}Y(s) = G(s)X(s) 或 G(s) = \frac{{Y(s)}}{{X(s)}}\end{array}\tag5 Y(s)=G(s)X(s)或G(s)=X(s)Y(s)(5)
式子(5)表明,在零初值条件下,系统的传递函数等于其响应的Laplace变换与其激励的Laplace变换之比。
因此,当我们知道系统的传递函数后,就可以由系统的激励按照式子(3)或式子(5)求出其响应的拉普拉斯变换 Y ( s ) Y(s) Y(s),再通过求逆变换可得其响应 y ( t ) y(t) y(t)。
系统的激励 x ( t ) x(t) x(t),系统的响应 y ( t ) y(t) y(t),以及它们的拉普拉斯变换 X ( s ) X(s) X(s), Y ( s ) Y(s) Y(s)和传递函数的关系如图1所示。
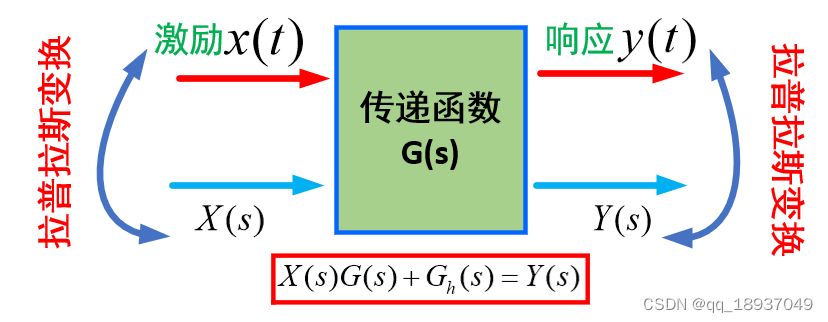
图1 系统激励、响应以及传递函数之间的关系
需要说明的是,传递函数不表明系统的物理性质。许多性质不同的物理系统,可以有相同的传递函数。而传递函数不同的物理系统,即使系统的激励相同,其响应也是不相同的,因此,对传递函数的分析和研究,就能统一处理各种物理性质不同的额线性系统。
简而言之,通过对系统微分方程进行拉普拉斯变换,推导出了系统的传递函数 G ( s ) G(s) G(s)。





—命名空间、缺省参数)













