1、概述
对于稀疏矩阵的解释,就是当矩阵里面零元素远远多于非零元素,且非零元素没有规律,这样的矩阵就叫做稀疏矩阵,反过来就是稠密矩阵,其中非零元素的数量与所有元素的比值叫做稠密度,一般稠密度小于0.05的都叫做稀疏矩阵。
我们知道压缩文件的时候,可以将大文件压缩成一个很小的文件,这是因为存在很多冗余,我们通过压缩算法将其进行压缩,同样的,既然矩阵里面存在很多零元素,我们也是可以将其剔除,这样就可以节省大量的存储空间了,而且可以提高计算的性能节约大量时间。其应用非常广泛,计算流体力学、统计物理、电路模拟、图像处理、纳米材料计算等。
2、压缩稀疏矩阵
那如何对其进行压缩以及还原呢,这里会将稀疏矩阵压缩成三个数组data、indptr、indices,让后通过这三个数组又可以进行还原成原来的矩阵。
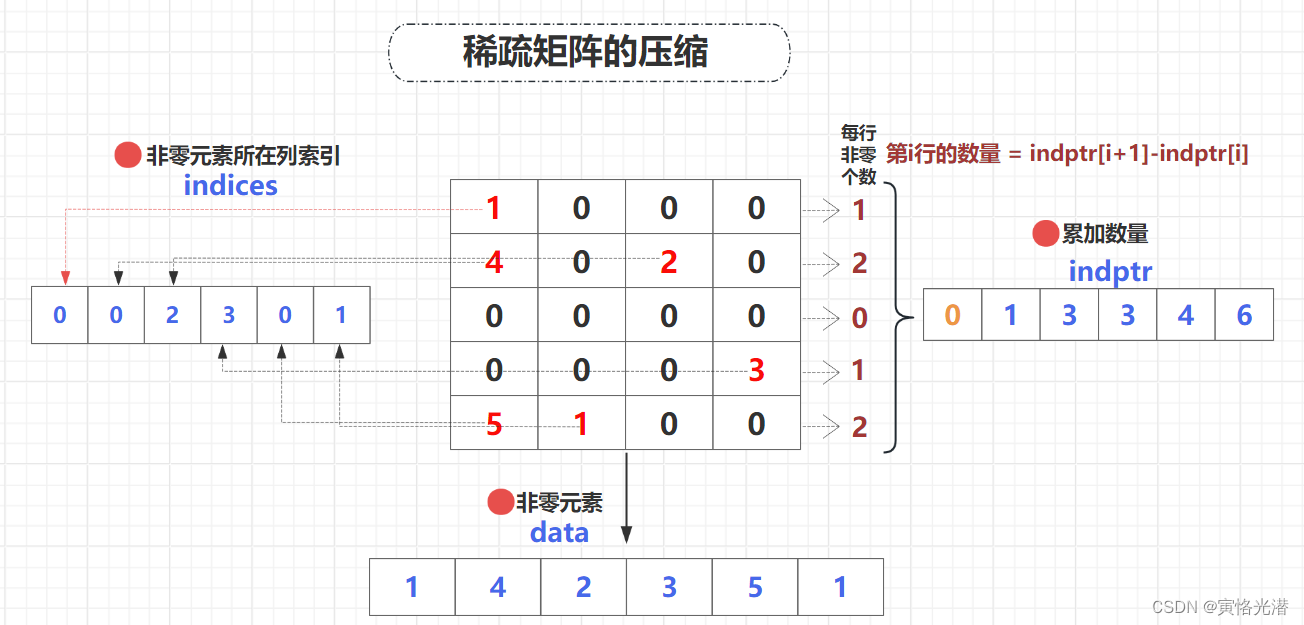
data:只存储非零元素
indptr:存储的是非零元素每行的累加数量,这样就能知道每行有多少个非零元素,当然这里为了计算每行的数量,也就是通过indptr[i+1] - indptr[i]可以计算到第i行的数量,为了便于计算第一行的数量,这里数组第一个元素设定为0
indices:存储非零元素所在列的索引值,这样就可以定位其在稀疏矩阵中的位置
通过这三个数组,我们就能够快速地找到任意非零元素的位置,从而进行矩阵运算和求解,大大减少计算时间。
我们通常会使用一种称为压缩稀疏行(Compressed Sparse Row,CSR)或者压缩稀疏矩阵(Compressed Sparse Matrix,CSM)的存储方式。
接下来我们看下载MXNet中的实际应用。
3、示例1
3.1、拆分稀疏矩阵
from mxnet import nd
import mxnet as mx
n1 = nd.array([[1,0,0,0],[4,0,2,0],[0,0,0,3],[5,1,0,0]])
/*
[[1. 0. 0. 0.][4. 0. 2. 0.][0. 0. 0. 3.][5. 1. 0. 0.]]
<NDArray 4x4 @cpu(0)>
*/稠密矩阵转换成稀疏矩阵
n1_csr = n1.tostype('csr')
<CSRNDArray 4x4 @cpu(0)>非零元素
n1_data = n1_csr.data
[1. 4. 2. 3. 5. 1.]
<NDArray 6 @cpu(0)>非零元素每行的累加数量
n1_indptr = n1_csr.indptr
[0 1 3 4 6]
<NDArray 5 @cpu(0)>这里就可以得到第几行有几个非零元素,比如第二行有两个非零元素,我们通过 n1_indptr[2]-n1_indptr[1] 即可获取。
非零元素的位置
n1_indices = n1_csr.indices
[0 0 2 3 0 1]
<NDArray 6 @cpu(0)>这样就将n1这样一个稀疏矩阵拆分成了三个数组,尤其是在实践中会经常碰见大的稀疏矩阵,这样拆分的小数组,就起到了很好的压缩的效果。
3.2、稀疏转换稠密
前面是稠密矩转换成稀疏矩阵,当然也可以将稀疏矩阵转换成稠密矩阵,两种方法,最简单的就是直接强制类型转换:
n1_csr.asnumpy()
array([[1., 0., 0., 0.],[4., 0., 2., 0.],[0., 0., 0., 3.],[5., 1., 0., 0.]], dtype=float32)另外一种方法就是将三个拆分的数组进行组合:
n1_o = nd.sparse.csr_matrix((n1_data, n1_indices, n1_indptr), shape = (4, 4))
n1_o.asnumpy()
array([[1., 0., 0., 0.],[4., 0., 2., 0.],[0., 0., 0., 3.],[5., 1., 0., 0.]], dtype=float32)这里还可以对形状进行指定,比如只截取3x3的矩阵:
n1_o = nd.sparse.csr_matrix((n1_data, n1_indices, n1_indptr), shape = (3,3))
n1_o.asnumpy()
array([[1., 0., 0.],[4., 0., 2.],[0., 0., 0.]], dtype=float32)也可以直接定义为稀疏矩阵:
src = nd.sparse.zeros('csr', (3,3))
<CSRNDArray 3x3 @cpu(0)>3.3、不同上下文比较
from mxnet import nd
import mxnet as mxx = nd.ones((2,3)) # 默认是CPU
y = x.as_in_context(mx.cpu())
z = x.as_in_context(mx.gpu())y is x # True
z is x # False就算它们的值是一样的,不在同一个上下文的值也是不能比较,这里很明显一个在CPU上计算,另一个是在GPU上计算。
4、示例2
再来看一个例子进行巩固下,后面也会以这个例子做一张图,了解稀疏矩阵的拆分原理。
也就是在上面例子增加一行全是0元素,这样就更加明白那个累加数量indptr的含义
from mxnet import nd
import mxnet as mxn2 = nd.array([[1,0,0,0],[4,0,2,0],[0,0,0,0],[0,0,0,3],[5,1,0,0]])
[[1. 0. 0. 0.][4. 0. 2. 0.][0. 0. 0. 0.][0. 0. 0. 3.][5. 1. 0. 0.]]
<NDArray 5x4 @cpu(0)>n2_csr = n2.tostype('csr')
<CSRNDArray 5x4 @cpu(0)>n2_data = n2_csr.data
[1. 4. 2. 3. 5. 1.]
<NDArray 6 @cpu(0)>n2_indptr = n2_csr.indptr
[0 1 3 3 4 6]
<NDArray 6 @cpu(0)>n2_indices = n2_csr.indices
[0 0 2 3 0 1]
<NDArray 6 @cpu(0)>5、图解
有了以上的介绍,应该都很熟悉这个稀疏矩阵,最后本人画了一张图,这样更能直观感受下稀疏矩阵拆分成三个数组的整个过程。

![算法刷题:P1025 [NOIP2001 提高组] 数的划分](http://pic.xiahunao.cn/算法刷题:P1025 [NOIP2001 提高组] 数的划分)





mnist手写数字分类识别的实现)





)





