2.1 线性代数
符号对照表

量子力学中,向量使用 ∣ ψ ⟩ \ket \psi ∣ψ⟩ (ket)来表示,可以理解为一个列向量。其对偶向量为 ⟨ ψ ∣ \bra \psi ⟨ψ∣ ,可以理解为行向量。
向量空间中零向量直接用 0 0 0 表示, ∣ 0 ⟩ \ket{0} ∣0⟩ 已有了其他含义。
2.1.1 基与线性无关
向量空间中的一个生成集是一组向量 ∣ v 1 ⟩ , ∣ v 2 ⟩ , . . . , ∣ v n ⟩ \ket{v_1},\ket{v_2},...,\ket{v_n} ∣v1⟩,∣v2⟩,...,∣vn⟩,空间中的任意向量 ∣ v ⟩ \ket{v} ∣v⟩ 均能使用该组向量的线性组合来表示,即 ∣ v ⟩ = ∑ i a i ∣ v i ⟩ \ket{v} = \sum_i a_i \ket{v_i} ∣v⟩=∑iai∣vi⟩。
线性相关
一组非零向量 ∣ v 1 ⟩ , ∣ v 2 ⟩ , . . . , ∣ v n ⟩ \ket{v_1},\ket{v_2},...,\ket{v_n} ∣v1⟩,∣v2⟩,...,∣vn⟩,如果存在一组复数 a 1 , a 2 , . . . , a n a_1, a_2,...,a_n a1,a2,...,an,其中至少对一个 i i i ,有 a i ≠ 0 a_i \ne 0 ai=0,
a 1 ∣ v 1 ⟩ + a 2 ∣ v 2 ⟩ + . . . + a n ∣ v n ⟩ = 0 a_1 \ket{v_1} + a_2 \ket{v_2} + ... + a_n \ket{v_n} = 0 a1∣v1⟩+a2∣v2⟩+...+an∣vn⟩=0
成立。反之,则是线性无关的。
对于任意两个线性无关的向量组如果都是向量空间 V V V 的生成集,则必然包含相同数目的元素。
2.1.2 线性算子与矩阵
定义
任意对输入是线性的函数 A : V → W A:V\rightarrow W A:V→W,满足:
A ( ∑ i a i ∣ ψ ⟩ ) = ∑ i a i A ∣ ψ ⟩ A(\sum_i a_i \ket{\psi}) = \sum_i a_i A \ket \psi A(i∑ai∣ψ⟩)=i∑aiA∣ψ⟩
线性算子与矩阵是等价的。
设 A : V → W A: V \rightarrow W A:V→W 是向量空间 V V V 和 W W W 之间的一个线性算子,设 ∣ v 1 ⟩ , ∣ v 2 ⟩ , . . . ∣ v m ⟩ \ket{v_1},\ket{v_2},...\ket{v_m} ∣v1⟩,∣v2⟩,...∣vm⟩ 是 V V V 的一个基而 ∣ w 1 ⟩ , ∣ w 2 ⟩ , . . . , ∣ w n ⟩ \ket{w_1},\ket{w_2},...,\ket{w_n} ∣w1⟩,∣w2⟩,...,∣wn⟩ 是 W W W 的一个基。于是存在
A ∣ v j ⟩ = ∑ i A i j ∣ w i ⟩ A \ket{v_j} = \sum_i A_{ij} \ket{w_i} A∣vj⟩=i∑Aij∣wi⟩
2.1.3 Pauli 阵

2.1.4 内积
内积定义
存在从 V × V V \times V V×V 到 C C C 的函数 ( ∙ , ∙ ) (\bullet,\bullet) (∙,∙),满足:
- ( ∙ , ∙ ) (\bullet,\bullet) (∙,∙) 对第二个自变量是线性的,即
( ∣ v ⟩ , ∑ i λ i ∣ w i ⟩ ) = ∑ i λ i ( ∣ v ⟩ , ∣ w i ⟩ ) (\ket{v}, \sum_i \lambda_i \ket{w_i}) = \sum_i \lambda_i(\ket v,\ket{w_i}) (∣v⟩,i∑λi∣wi⟩)=i∑λi(∣v⟩,∣wi⟩)
-
( ∣ v ⟩ , ∣ w ⟩ ) = ( ∣ w ⟩ , ∣ v ⟩ ) ∗ (\ket v, \ket w) = (\ket w, \ket v)^* (∣v⟩,∣w⟩)=(∣w⟩,∣v⟩)∗,即 ⟨ v ∣ w ⟩ = ( ⟨ w ∣ v ⟩ ) ∗ \braket{v|w} = (\braket{w|v})^* ⟨v∣w⟩=(⟨w∣v⟩)∗
-
( ∣ v ⟩ , ∣ v ⟩ ) ≥ 0 (\ket v, \ket v) \ge 0 (∣v⟩,∣v⟩)≥0, 当且仅当 ∣ v ⟩ = 0 \ket v = 0 ∣v⟩=0 时取等号
例如, C n C^n Cn 具有如下定义的一个内积:
( ( y 1 , y 2 , . . . y n ) , ( z 1 , z 2 , . . . , z n ) ) = ∑ i y i ∗ z i = [ y 1 ∗ , y 2 ∗ , . . . , y n ∗ ] [ z 1 z 2 ⋮ z n ] ((y_1,y_2,...y_n),(z_1,z_2,...,z_n)) = \sum_i y_i^*z_i = [y_1^*,y_2^*,...,y_n^*] \begin{bmatrix} z_1 \\ z_2 \\ \vdots \\ z_n \end{bmatrix} ((y1,y2,...yn),(z1,z2,...,zn))=i∑yi∗zi=[y1∗,y2∗,...,yn∗] z1z2⋮zn
带内积的向量空间称为内积空间,即 Hilbert 空间。
正交
如果向量 ∣ v ⟩ \ket v ∣v⟩ 和 ∣ w ⟩ \ket w ∣w⟩ 的内积为0,则称它们正交。
范数
∥ ∣ v ⟩ ∥ = ⟨ v ∣ v ⟩ \Vert \ket v \Vert = \sqrt{\braket{v|v}} ∥∣v⟩∥=⟨v∣v⟩
如果 ∥ ∣ v ⟩ ∥ = 1 \Vert \ket{v} \Vert = 1 ∥∣v⟩∥=1,则称其为单位向量,或归一化的。
对任意非零向量 ∣ v ⟩ \ket v ∣v⟩,向量除以其范数,称为向量的归一化。
从现在起,提到线性算子的矩阵表示时,我们总是指相对标准正交的输入输出基的矩阵表示,同时约定当线性算子的输入输出空间相同时,除非特别说明,输入输出基也取相同。
对偶向量可以当作一个行向量,其分量对于 ∣ v ⟩ \ket v ∣v⟩ 列向量表示的分量的复共轭,即 ⟨ v ∣ = [ v 1 ∗ , v 2 ∗ , . . . , v n ∗ ] \bra v = [v_1^*,v_2^*,...,v_n^*] ⟨v∣=[v1∗,v2∗,...,vn∗].
外积
设 ∣ v ⟩ \ket v ∣v⟩ 是内积空间 V V V 中的向量,而 ∣ w ⟩ \ket w ∣w⟩ 是内积空间 W W W 中的向量,定义 ∣ w ⟩ ⟨ v ∣ \ket w \bra v ∣w⟩⟨v∣ 为从 V V V 到 W W W 的线性算子:
( ∣ w ⟩ ⟨ v ∣ ) ( ∣ v ′ ⟩ ) = ∣ w ⟩ ⟨ v ∣ v ′ ⟩ = ⟨ v ∣ v ′ ⟩ ∣ w ⟩ (\ket w \bra v)(\ket {v^{'}}) = \ket w \braket {v|v^{'}} = \braket {v|v^{'}} \ket w (∣w⟩⟨v∣)(∣v′⟩)=∣w⟩⟨v∣v′⟩=⟨v∣v′⟩∣w⟩
完备性关系
设 i i i 为向量空间 V V V 的任意标准正交基,任意向量 ∣ v ⟩ \ket v ∣v⟩ 可写成 ∣ v ⟩ = ∑ i v i ∣ i ⟩ \ket v = \sum_i v_i \ket i ∣v⟩=∑ivi∣i⟩, v i v_i vi 是一组复数。注意到 ⟨ i ∣ v ⟩ = v i \braket {i|v} = v_i ⟨i∣v⟩=vi,于是
( ∑ i ∣ i ⟩ ⟨ i ∣ ) ∣ v ⟩ = ∑ i ∣ i ⟩ ⟨ i ∣ v ⟩ = ∑ i v i ∣ i ⟩ = ∣ v ⟩ (\sum_i \ket i \bra i) \ket v = \sum_i \ket i \braket {i | v} = \sum_i v_i \ket i = \ket v (i∑∣i⟩⟨i∣)∣v⟩=i∑∣i⟩⟨i∣v⟩=i∑vi∣i⟩=∣v⟩
故有:
∑ i ∣ i ⟩ ⟨ i ∣ = I \sum_i \ket i \bra i = I i∑∣i⟩⟨i∣=I
完备性关系的一个应用是把任意线性算子表示成外积形式。设 A : V → W A: V \rightarrow W A:V→W 是一个线性算子, ∣ v i ⟩ \ket{v_i} ∣vi⟩ 是 V V V 的一个标准正交基,且 w j w_j wj 是 W W W 的一个标准正交基,两次应用完备性关系得到:
A = I w A I v A = I_w A I_v A=IwAIv
= ∑ i j ∣ w j ⟩ ⟨ w j ∣ A ∣ v i ⟩ ⟨ v i ∣ = \sum_{ij}\ket{w_j} \bra{w_j} A \ket{v_i} \bra{v_i} =ij∑∣wj⟩⟨wj∣A∣vi⟩⟨vi∣
= ∑ i j ⟨ w j ∣ A ∣ v i ⟩ ∣ w j ⟩ ⟨ v i ∣ = \sum_{ij} \bra{w_j} A \ket{v_i} \ket{w_j}\bra{v_i} =ij∑⟨wj∣A∣vi⟩∣wj⟩⟨vi∣
这就是 A A A 的外积表示,从此式也可以看出相对输入基 ∣ v i ⟩ \ket{v_i} ∣vi⟩ 和 输出基 ∣ w ⟩ j \ket w_j ∣w⟩j , A A A 的第 i i i 列第 j j j 行元素是 ⟨ w j ∣ A ∣ v i ⟩ \bra{w_j}A\ket{v_i} ⟨wj∣A∣vi⟩.
2.1.5 特征向量和特征值
线性算子 A A A 在向量空间上的特征向量(本征向量,eigenvector)指非零的向量 ∣ v ⟩ \ket v ∣v⟩,使得 A ∣ v ⟩ = v ∣ v ⟩ A \ket v = v \ket v A∣v⟩=v∣v⟩,其中 v v v 是一个复数,称为 A A A 对应于 ∣ v ⟩ \ket v ∣v⟩ 的特征值(本征值,eigenvalue)。通常为方便起见,采用同一个记号 v v v 表示特征向量的标号和特征值。
向量空间 V V V 上算子 A A A 的对角表示是具有形式 A = ∑ i λ i ∣ i ⟩ ⟨ i ∣ A = \sum_i \lambda_i \ket i \bra i A=∑iλi∣i⟩⟨i∣ 的一个表示,其中向量组 ∣ i ⟩ \ket i ∣i⟩ 是 A A A 的特征向量构成的标准正交向量组,对应的特征值为 λ i \lambda_i λi。
如果一个算子有对角表示,它被称为可对角化。原矩阵与对角化后的矩阵是相似的。
当本征空间大于一维时,称为简并,即同一特征值对应多个线性无关的特征向量。
相似矩阵就是同一个线性变换在不同基下的矩阵表示
2.1.6 伴随与 Hermite 算子
伴随
设 A A A 是 Hilbert 空间 V V V 上的线性算子,实际上 V V V 上存在唯一的线性算子 A † A^{\dagger} A†,使得对所有向量 ∣ v ⟩ ∣ w ⟩ ∈ V \ket v \ket w \in V ∣v⟩∣w⟩∈V 成立:
( ∣ v ⟩ , A ∣ w ⟩ ) = ( A † ∣ v ⟩ , ∣ w ⟩ ) (\ket v, A \ket w) = (A^{\dagger}\ket v,\ket w) (∣v⟩,A∣w⟩)=(A†∣v⟩,∣w⟩)
即 ⟨ v ∣ A † w ⟩ = ⟨ A v ∣ w ⟩ = ⟨ w ∣ A v ⟩ ∗ \braket{v|A^{\dagger}w} = \braket{Av|w} = \braket{w|Av}^* ⟨v∣A†w⟩=⟨Av∣w⟩=⟨w∣Av⟩∗
这个线性算子称为 A A A 的伴随(adjoint)或 Hermite 共轭。如果 ∣ v ⟩ \ket v ∣v⟩ 是向量,则定义 ∣ v ⟩ † = ⟨ v ∣ \ket v ^{\dagger} = \bra v ∣v⟩†=⟨v∣.
性质:
- ( A B ) † = B † A † (AB)^{\dagger} = B^{\dagger}A^{\dagger} (AB)†=B†A† (从定义出发证明)
- ( ∣ w ⟩ ⟨ v ∣ ) † = ∣ v ⟩ ⟨ w ∣ (\ket w \bra v)^{\dagger} = \ket v \bra w (∣w⟩⟨v∣)†=∣v⟩⟨w∣ (用矩阵表示出来,Hermite 共轭运算的作用将矩阵变为共轭转置矩阵,即 A † = ( A ∗ ) T A^{\dagger} = (A^*)^T A†=(A∗)T)
- ( A ∣ v ⟩ ) † = ⟨ v ∣ † A † (A \ket v)^{\dagger} = \bra v^{\dagger} A^{\dagger} (A∣v⟩)†=⟨v∣†A†
- ( ∑ i a i A i ) † = ∑ i a i ∗ A i † (\sum_i a_iA_i)^{\dagger} = \sum_i a_i^* A_i^{\dagger} (∑iaiAi)†=∑iai∗Ai† (伴随的反线性)
- ( A † ) † = A (A^{\dagger})^{\dagger} = A (A†)†=A
厄密(自伴)算符:
如果 A † = A A^{\dagger} =A A†=A,即 ⟨ α ∣ A β ⟩ = ⟨ A α ∣ β ⟩ = ⟨ β ∣ A α ⟩ ∗ \braket{\alpha|A\beta} = \braket{A\alpha|\beta} = \braket{\beta|A\alpha}^* ⟨α∣Aβ⟩=⟨Aα∣β⟩=⟨β∣Aα⟩∗,则称 A A A 为 Hermite 或自伴算子。
从而 ⟨ α ∣ A α ⟩ = ⟨ A α ∣ α ⟩ = ⟨ α ∣ A α ⟩ ∗ \braket{\alpha|A\alpha} = \braket{A\alpha|\alpha} = \braket{\alpha|A\alpha}^* ⟨α∣Aα⟩=⟨Aα∣α⟩=⟨α∣Aα⟩∗,因此 ⟨ α ∣ A α ⟩ \braket{\alpha|A\alpha} ⟨α∣Aα⟩ 是实数。
也因此厄密算符 A A A 的对角元 A i i = ⟨ r i ∣ A r i ⟩ A_{ii} = \braket{r_i|Ar_i} Aii=⟨ri∣Ari⟩ 为实数。
⟨ r i ∣ A r j ⟩ = ⟨ A r i ∣ r j ⟩ = ⟨ r j ∣ A r i ⟩ ∗ \braket{r_i|Ar_j} = \braket{Ar_i|r_j}=\braket{r_j|Ar_i}^* ⟨ri∣Arj⟩=⟨Ari∣rj⟩=⟨rj∣Ari⟩∗,因此 A i j = A j i ∗ A_{ij} = A_{ji}^* Aij=Aji∗
投影算子
设 W W W 是 d d d 维向量空间 V V V 的 k k k 维算子,采用 Gram-Schimdt 过程,可以为 V V V 构造一个标准正交基 ∣ 1 ⟩ , . . . , ∣ d ⟩ \ket 1,...,\ket d ∣1⟩,...,∣d⟩, 使得 ∣ 1 ⟩ , . . . ∣ k ⟩ \ket 1,...\ket k ∣1⟩,...∣k⟩ 是 W W W 的一个标准正交基,定义
P = ∑ i k ∣ i ⟩ ⟨ i ∣ P = \sum_i^{k} \ket i \bra i P=i∑k∣i⟩⟨i∣
是 W W W 上的投影算子。
对任意向量 ∣ v ⟩ \ket v ∣v⟩, ∣ v ⟩ ⟨ v ∣ \ket v \bra v ∣v⟩⟨v∣ 都是厄密的,因此 P P P 也是厄密的,即 P † = P P^{\dagger} = P P†=P.
由完备性关系得, ∑ i ∣ i ⟩ ⟨ i ∣ = I \sum_i \ket i \bra i = I ∑i∣i⟩⟨i∣=I,因此 Q = I − P Q = I - P Q=I−P 为 P P P 的正交补.
对任意投影 P P P 满足 P 2 = P P^2 = P P2=P.
证明:
令 P = ∑ i ∣ i ⟩ ⟨ i ∣ P = \sum_i \ket i \bra i P=∑i∣i⟩⟨i∣,则 P 2 = ∑ i j ∣ i ⟩ ⟨ i ∣ j ⟩ ⟨ j ∣ = ∑ i j δ i j ⟨ i ∣ j ⟩ = ∑ i ∣ i ⟩ ⟨ i ∣ = P P^2 = \sum_{ij}\ket i \braket {i | j} \bra j = \sum_{ij} \delta_{ij}\braket{i|j} = \sum_i \ket i \bra i = P P2=∑ij∣i⟩⟨i∣j⟩⟨j∣=∑ijδij⟨i∣j⟩=∑i∣i⟩⟨i∣=P.
正规算子
算子 A A A 称为正规的,如果 A A † = A † A AA^{\dagger} = A^{\dagger}A AA†=A†A 成立。
性质:
- 正规矩阵是厄密的,当且仅当它的特征值为实数。
谱分解定理
一个算子是正规算子当且仅当它可对角化。
任意正规矩阵都可在经过一个酉变换后变为对角矩阵,反过来所有可在经过一个酉变换后变为对角矩阵的矩阵都是正规矩阵。
酉矩阵
满足 U U † = U † U = I UU^{\dagger} = U^{\dagger}U = I UU†=U†U=I。
-
U − 1 = U † U^{-1} = U^{\dagger} U−1=U†,且 U † U^{\dagger} U† 也是幺正算符
-
U U U 是正规的且有谱分解。
-
幺正算符的乘积也是幺正:
( U V ) ( U V ) † = U V V † U † = I (UV)(UV)^{\dagger} = UVV^{\dagger}U^{\dagger} = I (UV)(UV)†=UVV†U†=I
-
幺正算符保持两个算符内积不变:
⟨ U α ∣ U β ⟩ = ⟨ α ∣ U † U β ⟩ = ⟨ α ∣ β ⟩ \braket{U\alpha|U\beta} = \braket{\alpha|U^{\dagger}U\beta} = \braket{\alpha | \beta} ⟨Uα∣Uβ⟩=⟨α∣U†Uβ⟩=⟨α∣β⟩
-
幺正算符是正交矩阵(比如空间中的转动)的推广。相互正交的向量作相同转动后仍然正交。
-
∣ ψ ( t ) ⟩ = U ( t ) ∣ ψ ( 0 ) ⟩ \ket{\psi(t)} = U(t)\ket{\psi(0)} ∣ψ(t)⟩=U(t)∣ψ(0)⟩ 中的演化算符 U ( t ) U(t) U(t) 是幺正的。
谱分解定理证明
2.1.7 张量积
张量积是将向量空间合在一起,构成更大向量空间的一种方法。
设 V V V 和 W W W 是维数分别是 m m m 和 n n n 的向量空间,并假定 V V V 和 W W W 是 Hilbert 空间,于是 V ⊗ W V \otimes W V⊗W 是一个 m n mn mn 维向量空间。 V ⊗ W V \otimes W V⊗W 的元素是 V V V 的元素 ∣ v ⟩ \ket v ∣v⟩ 和 W W W 的元素 ∣ w ⟩ \ket w ∣w⟩ 的张量积 ∣ v ⟩ ⊗ ∣ w ⟩ \ket v \otimes \ket w ∣v⟩⊗∣w⟩ 的线性组合。如果 ∣ i ⟩ \ket i ∣i⟩ 和 ∣ j ⟩ \ket j ∣j⟩ 是 V V V 和 W W W 的标准正交基,则 ∣ i ⟩ ⊗ ∣ j ⟩ \ket i \otimes \ket j ∣i⟩⊗∣j⟩ 是 V ⊗ W V\otimes W V⊗W 的一个基。
性质:
- 对任意标量 z z z, V V V 的元素 v v v 和 W W W 的元素 w w w,满足 z ( ∣ v ⟩ ⊗ ∣ w ⟩ ) = ( z ∣ v ⟩ ) ⊗ ∣ w ⟩ = ∣ v ⟩ ⊗ ( z ∣ w ⟩ ) z(\ket v \otimes \ket w) = (z\ket v) \otimes \ket w = \ket v \otimes (z\ket w) z(∣v⟩⊗∣w⟩)=(z∣v⟩)⊗∣w⟩=∣v⟩⊗(z∣w⟩).
- 对 V V V 中任意的 v 1 v_1 v1 和 v 2 v_2 v2 和 W W W 中的 ∣ w ⟩ \ket w ∣w⟩,满足 ( ∣ v 1 ⟩ + ∣ v 2 ⟩ ) ⊗ ∣ w ⟩ = ∣ v 1 ⟩ ⊗ ∣ w ⟩ + ∣ v 2 ⟩ ⊗ ∣ w ⟩ (\ket {v_1} + \ket {v_2}) \otimes \ket w = \ket {v_1} \otimes \ket w + \ket {v_2} \otimes \ket w (∣v1⟩+∣v2⟩)⊗∣w⟩=∣v1⟩⊗∣w⟩+∣v2⟩⊗∣w⟩.
- 对 V V V 中任意的 ∣ v ⟩ \ket v ∣v⟩ 和 W W W 中的 w 1 w_1 w1 和 w 2 w_2 w2,满足 ∣ v ⟩ ⊗ ( ∣ w 1 ⟩ + ∣ w 2 ⟩ ) = ∣ v ⟩ ⊗ ∣ w 1 ⟩ + ∣ v ⟩ ⊗ ∣ w 2 ⟩ \ket v \otimes (\ket {w_1} + \ket {w_2}) = \ket v \otimes \ket {w_1} + \ket v \otimes \ket {w_2} ∣v⟩⊗(∣w1⟩+∣w2⟩)=∣v⟩⊗∣w1⟩+∣v⟩⊗∣w2⟩.
矩阵表示
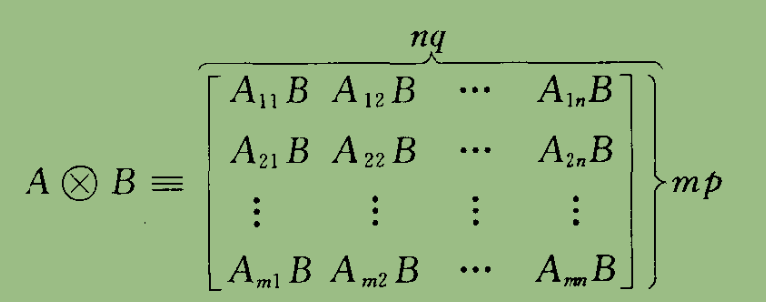
2.1.8 算子函数
定义
T r ( A ) = ∑ i = 1 n A i i Tr(A) = \sum_{i=1}^nA_{ii} Tr(A)=i=1∑nAii
如果有一组正交单位特征基 { ∣ i ⟩ } \{\ket i\} {∣i⟩},则存在 T r ( A ) = ∑ i ⟨ i ∣ A ∣ i ⟩ Tr(A) = \sum_i \bra i A \ket i Tr(A)=∑i⟨i∣A∣i⟩.
性质
-
T r ( A + B ) = T r ( A ) + T r ( B ) Tr(A+B) = Tr(A) + Tr(B) Tr(A+B)=Tr(A)+Tr(B)
-
T r ( c A ) = c T r ( A ) Tr(cA) = cTr(A) Tr(cA)=cTr(A)
-
T r ( A B ) = T r ( B A ) Tr(AB) = Tr(BA) Tr(AB)=Tr(BA)
证明
T r ( A B ) = ∑ i ⟨ i ∣ A B ∣ i ⟩ = ∑ i k ⟨ i ∣ A ∣ k ⟩ ⟨ k ∣ B ∣ i ⟩ = ∑ i k ⟨ k ∣ B ∣ i ⟩ ⟨ i ∣ A ∣ k ⟩ = ∑ k ⟨ k ∣ B A ∣ k ⟩ = T r ( B A ) Tr(AB) = \sum_i \bra i A B \ket i = \sum_{ik} \bra i A \ket k \bra k B \ket i = \sum_{ik}\bra k B \ket i \bra i A \ket k = \sum_k \bra k BA \ket k = Tr(BA) Tr(AB)=∑i⟨i∣AB∣i⟩=∑ik⟨i∣A∣k⟩⟨k∣B∣i⟩=∑ik⟨k∣B∣i⟩⟨i∣A∣k⟩=∑k⟨k∣BA∣k⟩=Tr(BA)
-
T r ( A 1 A 2 . . . A n ) = T r ( A 2 A 3 . . . A n A 1 ) = . . . = T r ( A n A 1 . . . A n − 1 ) Tr(A_1A_2...A_n) = Tr(A_2A_3...A_nA_1) = ... = Tr(A_nA_1...A_{n-1}) Tr(A1A2...An)=Tr(A2A3...AnA1)=...=Tr(AnA1...An−1)
迹与表象选择无关:选取 { ∣ i ⟩ } \{\ket i\} {∣i⟩} 和 { ∣ j ⟩ } \{\ket j\} {∣j⟩} 两组基, ∑ i ⟨ i ∣ A ∣ i ⟩ = ∑ i j ⟨ i ∣ j ⟩ ⟨ j ∣ A ∣ i ⟩ = ∑ i j ⟨ j ∣ A ∣ i ⟩ ⟨ i ∣ j ⟩ = ∑ j ⟨ j ∣ A ∣ j ⟩ \sum_i \bra{i} A \ket i = \sum_{ij}\braket {i|j} \bra j A \ket i = \sum_{ij} \bra j A \ket i \braket {i|j} = \sum_j \bra j A \ket j ∑i⟨i∣A∣i⟩=∑ij⟨i∣j⟩⟨j∣A∣i⟩=∑ij⟨j∣A∣i⟩⟨i∣j⟩=∑j⟨j∣A∣j⟩.
任何幺正算符 U U U:
T r ( U † A U ) = T r ( U U † A ) = T r ( A ) Tr(U^{\dagger}AU) = Tr(UU^{\dagger}A) = Tr(A) Tr(U†AU)=Tr(UU†A)=Tr(A)
算符期望值可写成迹:
T r ( A ∣ α ⟩ ⟨ α ∣ ) = ∑ i ⟨ i ∣ A ∣ α ⟩ ⟨ α ∣ i ⟩ = ∑ i ⟨ α ∣ i ⟩ ⟨ i ∣ A ∣ α ⟩ = ⟨ α ∣ A ∣ α ⟩ Tr(A\ket \alpha \bra \alpha) = \sum_i \bra i A \ket \alpha \braket {\alpha|i} = \sum_i \braket{\alpha|i}\bra i A \ket \alpha = \bra \alpha A \ket \alpha Tr(A∣α⟩⟨α∣)=i∑⟨i∣A∣α⟩⟨α∣i⟩=i∑⟨α∣i⟩⟨i∣A∣α⟩=⟨α∣A∣α⟩
∣ ψ ⟩ \ket \psi ∣ψ⟩ 扩展成一个以 ψ \psi ψ 为首个元的标准正交基 ∣ i ⟩ \ket i ∣i⟩,因此 ⟨ α ∣ i ⟩ = δ α i \braket {\alpha|i} = \delta_{\alpha i} ⟨α∣i⟩=δαi.
2.1.9 对易式和反对易式
两个算子 A A A 和 B B B 之间的对易式定义为 [ A , B ] = A B − B A [A,B]=AB-BA [A,B]=AB−BA.
若 A B = B A AB = BA AB=BA,则说明 A A A 和 B B B 是对易的。
两个算子 A A A 和 B B B 的反对易式定义为 { A , B } = A B + B A \{A,B\} = AB + BA {A,B}=AB+BA.
若 { A , B } = 0 \{A,B\} = 0 {A,B}=0,则说明 A A A 和 B B B 反对易。
同时对角化定理
设 A A A 和 B B B 是厄密算子,当且仅当存在一个标准正交基,使 A A A 和 B B B 在这个基下同时是对角的,则 [ A , B ] = 0 [A,B] = 0 [A,B]=0.在这种情况下, A A A 和 B B B 称为可同时对角化。
Gram-Schmidt正交化(构造正交归一基)
考虑完备集 { ∣ α 1 ⟩ , ∣ α 2 ⟩ , . . . , ∣ α n ⟩ } \{\ket{\alpha_1},\ket{\alpha_2},...,\ket{\alpha_n}\} {∣α1⟩,∣α2⟩,...,∣αn⟩}.
∣ β 1 ⟩ = ∣ α 1 ⟩ \ket{\beta_1} = \ket{\alpha_1} ∣β1⟩=∣α1⟩.
∣ β i ⟩ = ∣ α i ⟩ − P 1... i − 1 ∣ α i ⟩ \ket{\beta_i} = \ket{\alpha_i} - P_{1...i-1}\ket{\alpha_i} ∣βi⟩=∣αi⟩−P1...i−1∣αi⟩ (从 α i \alpha_i αi 中去除其在 ∣ β 1 ⟩ , . . . , ∣ β i − 1 ⟩ \ket{\beta_1},...,\ket{\beta_{i-1}} ∣β1⟩,...,∣βi−1⟩ 上的分量)
其中 P 1... i − 1 = ∑ k = 1 i − 1 ∣ β ′ ⟩ ⟨ β ′ ∣ P_{1...i-1} = \sum_{k=1}^{i-1}\ket{\beta^{'}}\bra{\beta^{'}} P1...i−1=∑k=1i−1∣β′⟩⟨β′∣ 是 ∣ β 1 ′ ⟩ , . . . , ∣ β i − 1 ′ ⟩ \ket{\beta^{'}_1},...,\ket{\beta^{'}_{i-1}} ∣β1′⟩,...,∣βi−1′⟩ 张成的子空间的投影算符。
可以得到 ∣ β i ⟩ = ∣ α i ⟩ − ∑ k = 1 i − 1 ⟨ β k ∣ α i ⟩ ⟨ β k ∣ β k ⟩ ∣ β k ⟩ \ket{\beta_i} = \ket{\alpha_i} - \sum_{k=1}^{i-1}\frac{\braket{\beta_k|\alpha_i}}{\braket{\beta_k|\beta_k}}\ket{\beta_k} ∣βi⟩=∣αi⟩−∑k=1i−1⟨βk∣βk⟩⟨βk∣αi⟩∣βk⟩
β ′ = ∣ β i ⟩ ∣ ∣ ∣ β i ⟩ ∣ ∣ , i = 1 , 2 , . . . , n \beta^{'} = \frac{\ket{\beta_i}}{||\ket{\beta_i}||}, i=1,2,...,n β′=∣∣∣βi⟩∣∣∣βi⟩,i=1,2,...,n 正交归一基。
完备性关系
已知 α i \alpha_i αi 是 ∣ α ⟩ \ket{\alpha} ∣α⟩ 的基向量, a i = ⟨ α i ∣ α ⟩ a_i = \braket{\alpha_i|\alpha} ai=⟨αi∣α⟩, ∑ i ∣ α i ⟩ ⟨ α i ∣ = I \sum_i \ket{\alpha_i}\bra{\alpha_i} = I ∑i∣αi⟩⟨αi∣=I.
证明: ( ∑ i ∣ α i ⟩ ⟨ α i ∣ ) ∣ α ⟩ = ∑ i ∣ α i ⟩ ⟨ α i ∣ α ⟩ = ∑ i a i ∣ α i ⟩ = ∣ α ⟩ (\sum_i \ket{\alpha_i}\bra{\alpha_i})\ \ket{\alpha} = \sum_i\ket{\alpha_i}\braket{\alpha_i|\alpha} = \sum_i a_i \ket{\alpha_i} = \ket{\alpha} (∑i∣αi⟩⟨αi∣) ∣α⟩=∑i∣αi⟩⟨αi∣α⟩=∑iai∣αi⟩=∣α⟩,因此 ∑ i ∣ α i ⟩ ⟨ α i ∣ = I \sum_i \ket{\alpha_i}\bra{\alpha_i} = I ∑i∣αi⟩⟨αi∣=I.
)

 重磅更新!黑入工业PLC设备!)

)



——接口)


)
——相机基础)


)
上部署静态网站)
位置、Mono打包输出的dll(程序集)位置)

