- 一、题目
- 二、数据合并、清洗、描述性统计
- 1、数据获取
- 2、数据合并
- 3、选择董监高薪酬作为解释变量的理论逻辑分析
- 三、多元回归模型的参数估计、结果展示与分析
- 1、描述性统计分析
- 2、剔除金融类上市公司
- 3、对所有变量进行1%缩尾处理
- 4、0-1标准化,所有解释变量
- 5、绘制热力图
- 6、逐步加入关键解释变量
- 7、制作显著性表格
- 8、经典logit回归
- 首先,一件非常崩溃的事情,昨天晚上使用jupyter notebook跑的数据、代码全部没了,非常难受。
- 不过好在自己
足够坚强,反思了一下,当时要关闭的时候显示未保存,但是明明自己保存了,所以还是自己的问题。其次,我懂得了以后使用jupyter notebook 会更加小心谨慎。 - 过一段重装一下,看看是什么原因导致无法正常保存。
一、题目

- 四个文件的资料已经放在Q群里面了
二、数据合并、清洗、描述性统计
1、数据获取
- 从CSMAR【国泰安金融数据库】数据库下载上市公司基本信息、个股日度收益率、公司董监高等高管个人资料(含个人特征、兼任信息、总经理变更等)、关联交易or股权质押or交叉持股情况、财务指标(包括比率结构、相对价值指标、盈利能力指标)
- 当然,我实际用到的数据没有那么多,就4个表格。
df1数据如下:
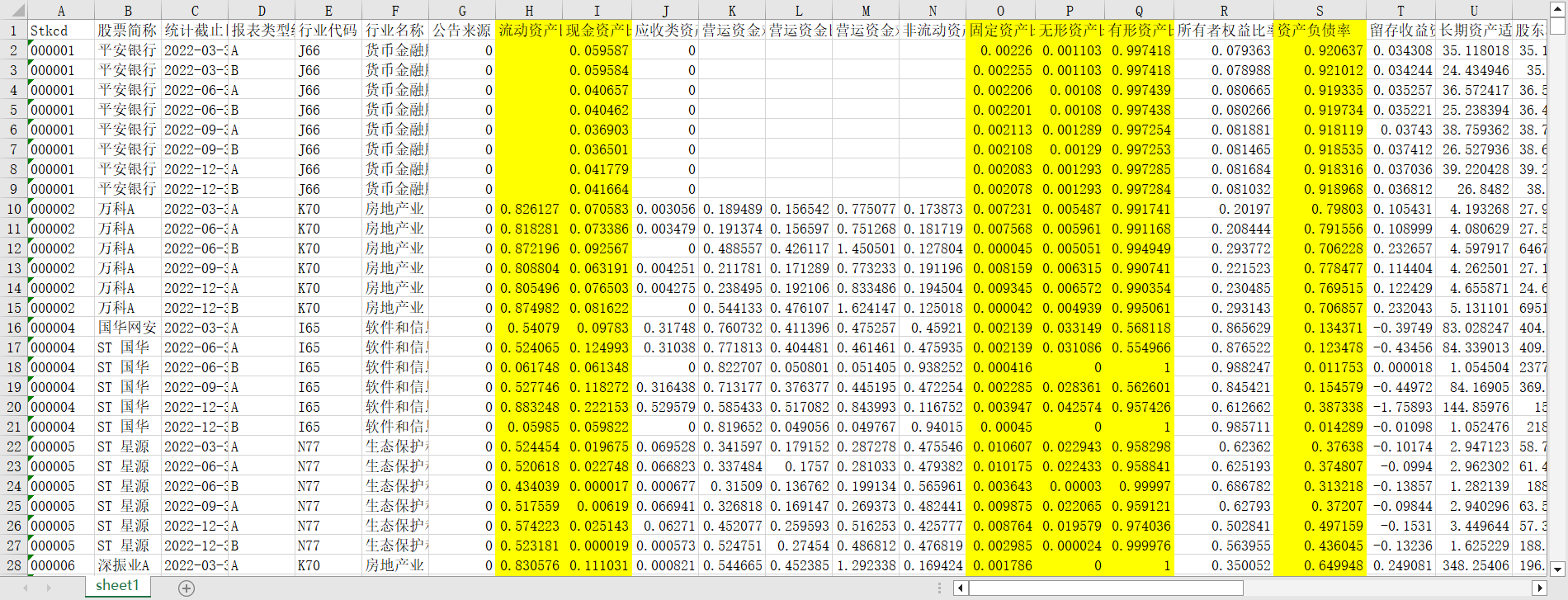
df2数据如下:
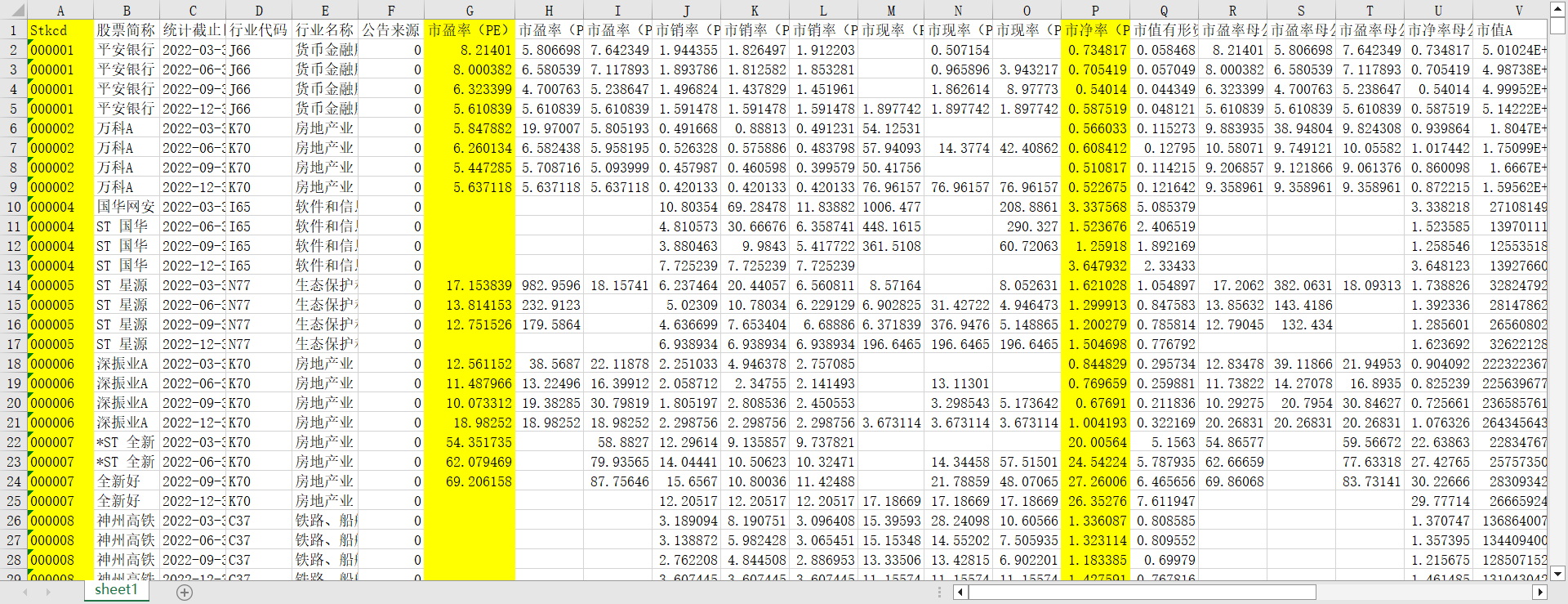
df3数据如下:

df4数据如下:
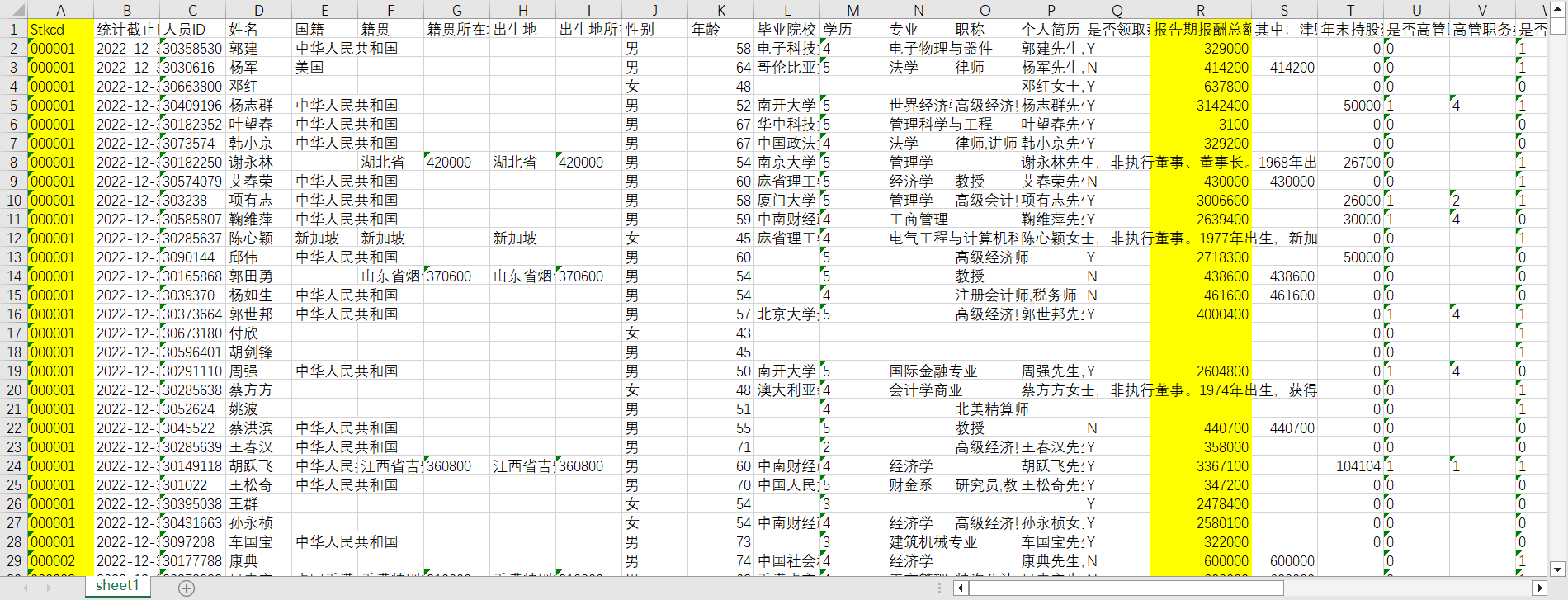
- df4的数据我只使用了报告期薪酬这列数据,与上面的三张表格的部分数据进行合并。
- 此外发现统计截止日期都是同一个日期,因此需要进行处理。
2、数据合并
from scipy.stats.mstats import winsorize
import statsmodels.api as sma
from sklearn.preprocessing import MinMaxScaler # min-max 标准化
import pandas as pd
import numpy as np
df1=pd.read_excel("比例结构.xlsx")
df2=pd.read_excel("相对价值指标.xlsx")
df3=pd.read_excel("盈利能力.xlsx")
df4=pd.read_excel("副本董监高个人特征文件.xlsx")
# 删除'报告期报酬总额'列为空的行
df4 = df4[df4['报告期报酬总额']>0]
import pandas as pd# 假设df1, df2, df3已经被创建并且包含了相应的列# 首先,合并df1和df2
data1 = pd.merge(df1[['Stkcd', '股票简称', '统计截止日期', '流动资产比率', '现金资产比率', '固定资产比率', '无形资产比率', '有形资产比率', '资产负债率','归属于母公司净利润占比', '主营业务利润占比']], df2[['Stkcd', '股票简称', '统计截止日期', '市盈率(PE)1', '市净率母公司(PB)', '托宾Q值B', '账面市值比A']], on=['Stkcd', '股票简称', '统计截止日期'], how='inner')# 然后,将df4与df3合并
data1 = pd.merge(data1, df3[['Stkcd', '股票简称', '统计截止日期', '销售费用率', '管理费用率', '总资产净利润率(ROA)A']], on=['Stkcd', '股票简称', '统计截止日期'], how='inner')# 现在df4包含了所有需要的列
# 缺失值直接去除
data1=data1.dropna()
data1
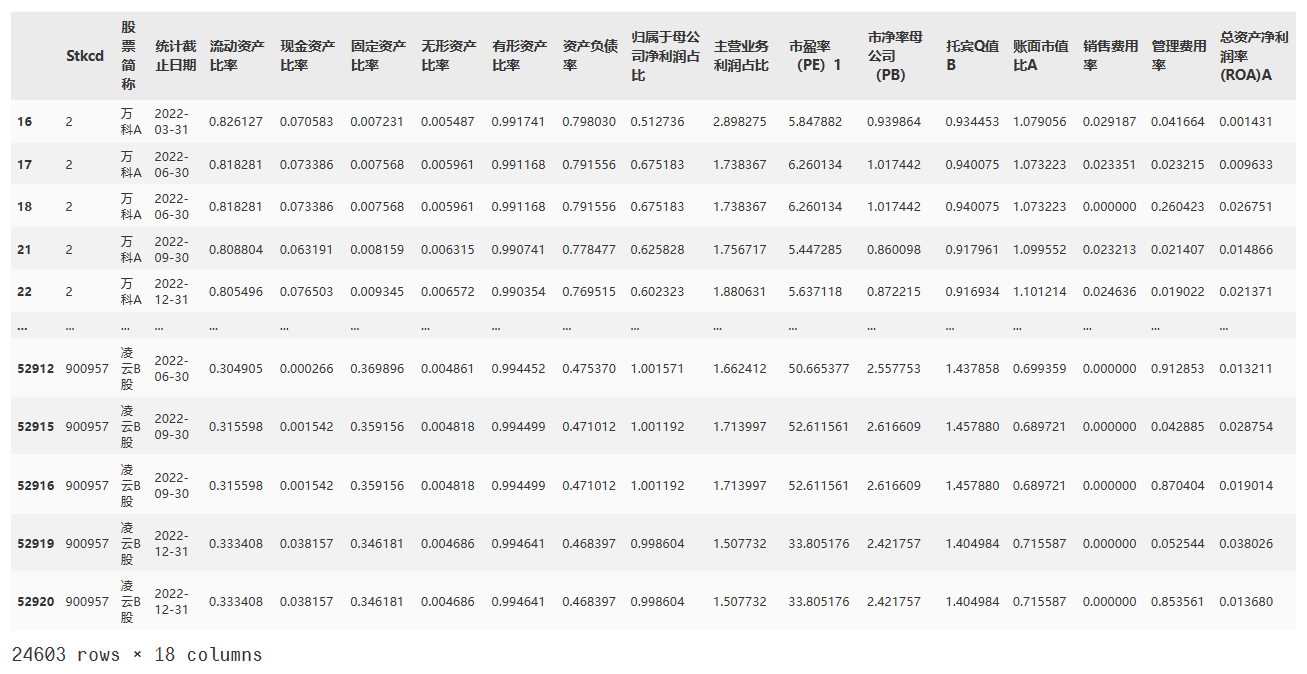
# 对df4的数据进行处理,使用groupby和agg进行聚合操作
df44 = df4.groupby(['Stkcd', '统计截止日期']).agg({'报告期报酬总额': ['sum', 'count']})# 重命名列名
df44.columns = ['总和', '计数']# 计算均值
df44['均值'] = df44['总和'] / df44['计数']# 重置索引以获得所需的结果
df44.reset_index(inplace=True)
df44 = pd.DataFrame(df44)
df44
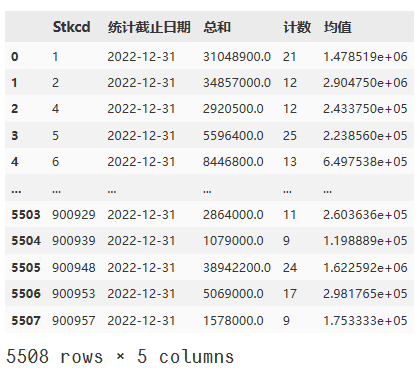
# 然后,将df4与df3合并
data1 = pd.merge(data1, df44[['Stkcd', '均值']], on=['Stkcd'], how='inner')
data1
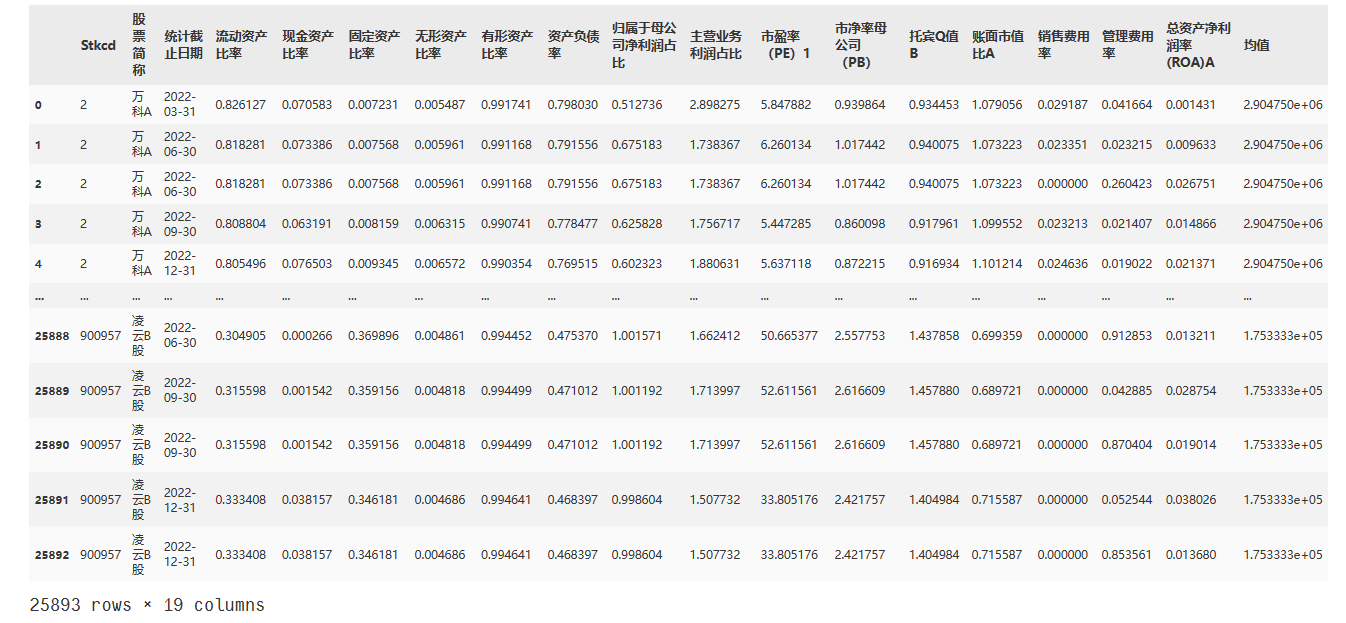
data1.rename(columns={'均值': '董监高报告期报酬均值'}, inplace=True)
data1.columns
data1.isnull().sum()
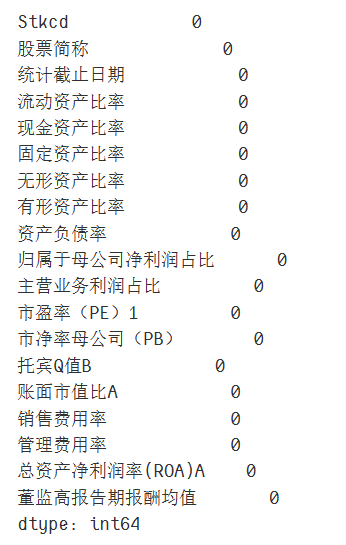
被解释变量:
- 总资产净利润率(ROA)A :指的是企业总资产的净利润率,是一种衡量公司经营效率的财务指标。
解释变量:
-
流动资产比率:流动资产比率是指企业流动资产与总资产的比例,反映了企业流动性的程度。
-
现金资产比率:现金资产比率是指企业现金资产与总资产的比例,反映了企业现金储备的情况。
-
固定资产比率:固定资产比率是指企业固定资产与总资产的比例,反映了企业固定资产在总资产中的占比。
-
有形资产比率:有形资产比率是指企业有形资产与总资产的比例,有形资产指的是可以触摸和看到的资产,如土地、建筑物等。
-
无形资产比率:无形资产比率是指企业无形资产与总资产的比例,无形资产指的是无形的资产,如专利、商标等。
-
资产负债率:资产负债率是指企业负债总额与总资产的比例,反映了企业负债的程度。
-
管理费用率:管理费用率是指企业管理费用与营业收入的比例,反映了企业管理费用在营业收入中的占比。
-
销售费用率:销售费用率是指企业销售费用与营业收入的比例,反映了企业销售费用在营业收入中的占比。
-
归属于母公司净利润占比:归属于母公司净利润占比是指企业归属于母公司的净利润与净利润的比例,反映了母公司对净利润的占有程度。
-
主营业务利润占比:主营业务利润占比是指企业主营业务利润与净利润的比例,反映了主营业务对净利润的贡献程度。
-
董监高报告期报酬均值:董监高报告期报酬均值是指企业董事、监事和高级管理人员在报告期内的平均报酬水平。
3、选择董监高薪酬作为解释变量的理论逻辑分析
- 吴育辉(2010)以 2004—2008 年我国全部 A 股上研究对象,发现高管薪酬与公司 ROA 显著正相关。张燕红(2016)和蒋泽芳(2019)的研究结果也证明高管薪酬激励对企业经营业绩存在显著正向影响。
- [1] 吴育辉,吴世农.高管薪酬:激励还是自利[J].会计研究,2010(11):40-48+96-97.
- [2]张燕红.高管薪酬激励对企业绩效的影响[J].经济问题,2016(06):116-120.
- [3]蒋泽芳,陈祖英.高管薪酬、股权集中度与企业绩效[J].财会通讯,2019(18):64-68.
三、多元回归模型的参数估计、结果展示与分析
1、描述性统计分析
xVars =['流动资产比率', '现金资产比率', '固定资产比率', '有形资产比率', '无形资产比率','资产负债率', '管理费用率', '销售费用率', '归属于母公司净利润占比', '主营业务利润占比', '董监高报告期报酬均值']
yVar = ['总资产净利润率(ROA)A']
xyVars = yVar + xVars
perct = [0.005,0.01,0.02,0.03, 0.04, 0.05, 0.1,0.15,0.25]
perct += [1-a for a in perct]
perct += [0.5]
sorted(perct)
data1[xVars].describe(percentiles = perct)
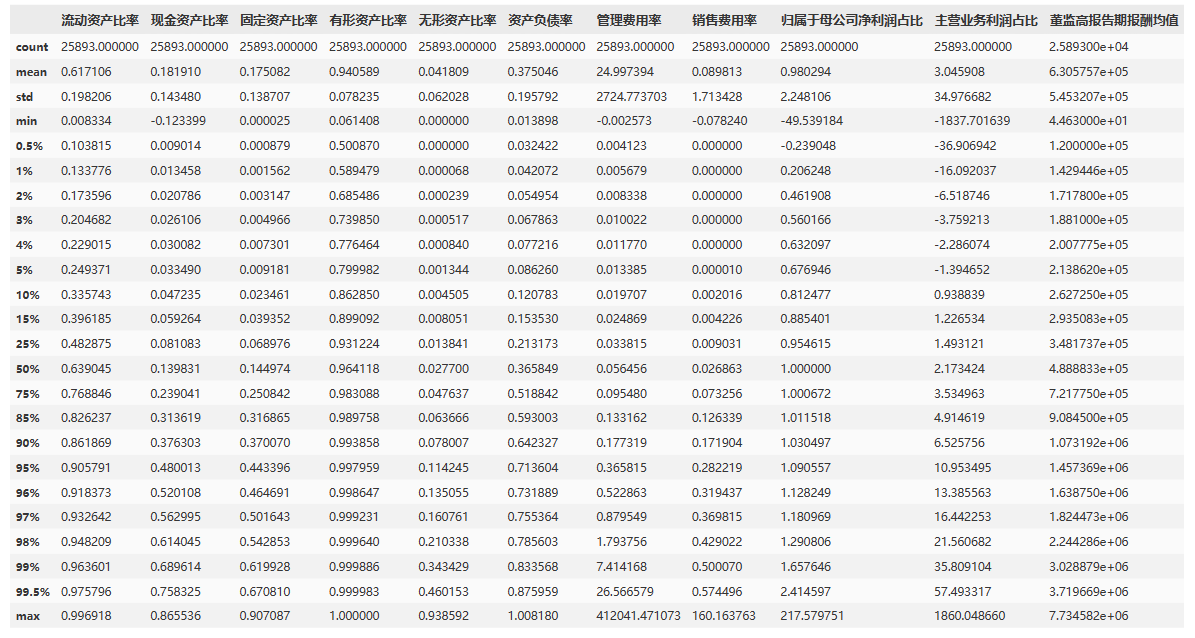
结合上面的描述性统计结果,可以看出:
- 流动资产比率:流动资产比率最小值为0.008334,最大值为0.996918,中位数为0.639045。
- 现金资产比率:现金资产比率最小值为-0.123399,最大值为0.865536,中位数为0.139831。
- 固定资产比率:固定资产比率最小值为0.000025,最大值为0.907087,中位数为0.144974。
- 有形资产比率:有形资产比率最小值为0.061408,最大值为1,中位数为0.964118。
- 无形资产比率:无形资产比率最小值为0,最大值为0.938592,中位数为0.0277。
- 资产负债率:资产负债率最小值为0.013898,最大值为1.00818,中位数为0.365849。最大值接近1可能表示某些公司存在高度杠杆,这可能是金融机构的特点。因此,剔除上市公司当中的金融机构以减小金融机构对分析的影响。
- 管理费用率:管理费用率最小值为-0.002573,最大值为412041.4711,中位数为0.056456。
- 销售费用率:销售费用率最小值为-0.07824,最大值为160.163763,中位数为0.026863。
- 归属于母公司净利润占比:归属于母公司净利润占比最小值为-49.539184,最大值为217.579751,中位数为1。
- 主营业务利润占比:主营业务利润占比最小值为-1837.701639,最大值为1860.04866,中位数为2.173424。
- 董监高报告期报酬均值:董监高报告期报酬均值最小值为4.46E+01,最大值为7734582.353,中位数为4.89E+05。
2、剔除金融类上市公司
data1 = data1[~data1['股票简称'].str.contains('金融')]
data1
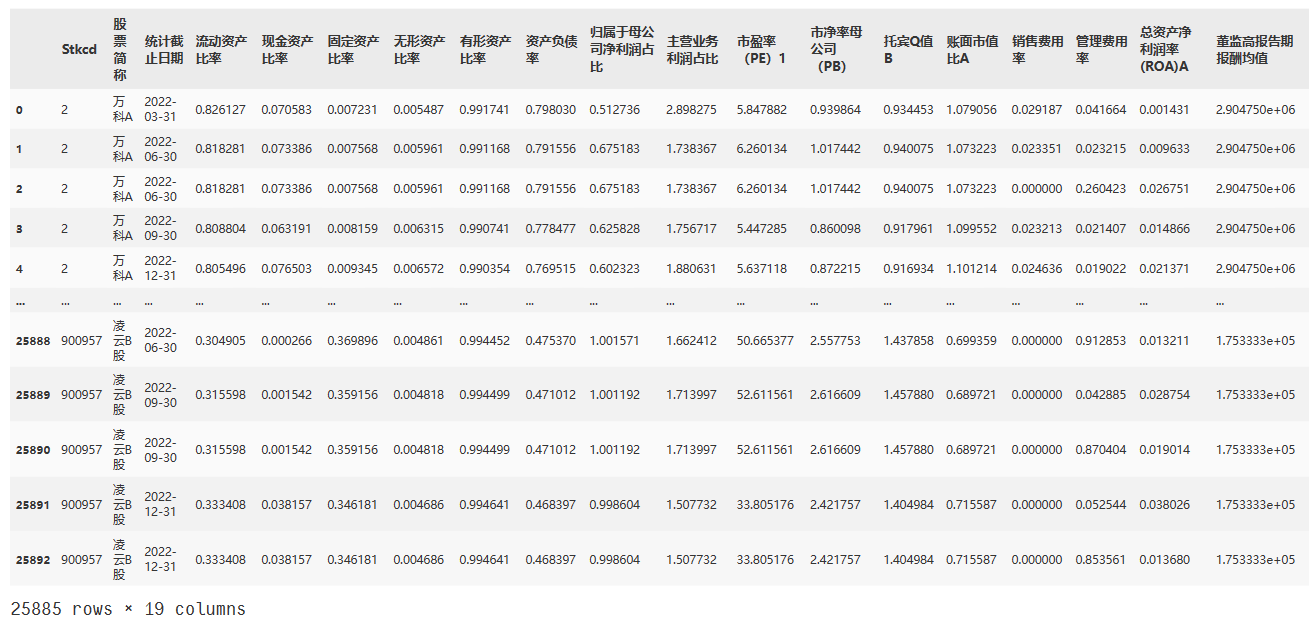
- 注:其实就减少了几条数据而已
3、对所有变量进行1%缩尾处理
cols_to_winsorize = ['流动资产比率', '现金资产比率', '固定资产比率', '有形资产比率', '无形资产比率','资产负债率', '管理费用率', '销售费用率', '归属于母公司净利润占比', '主营业务利润占比', '董监高报告期报酬均值']# 对每个变量进行缩尾处理
for col in cols_to_winsorize:data1[col] = winsorize(data1[col], limits=(0.01, 0.01))
data1[xVars].describe(percentiles = perct)
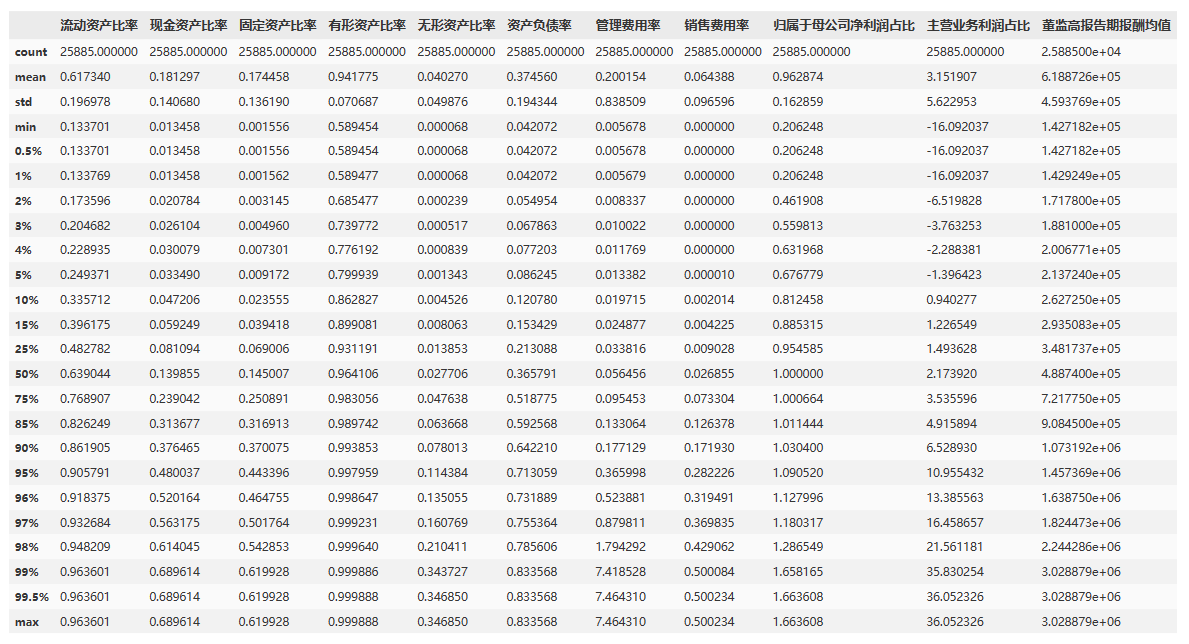
4、0-1标准化,所有解释变量
data1[xVars] = MinMaxScaler().fit_transform(data1[xVars])
data1[xVars].describe()
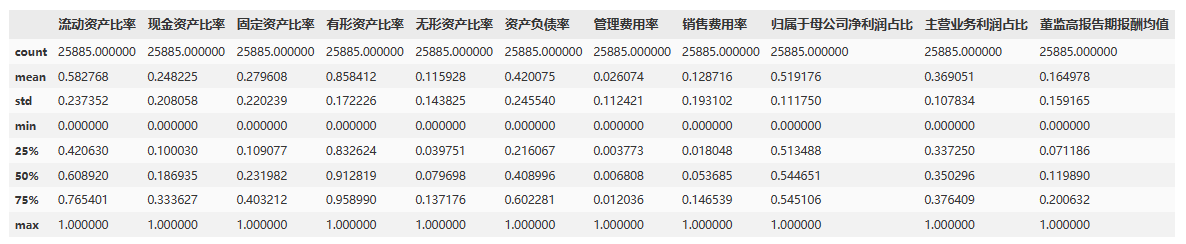
5、绘制热力图
import matplotlib.pyplot as plt
import seaborn as sns # 画热度图
plt.rcParams["font.sans-serif"] = ["SimHei"] #设置字体
plt.rcParams["axes.unicode_minus"] = False #该语句解决图像中的“-”负号的乱码问题
a = data1[xVars].corr()
plt.figure(figsize=(10, 8)) # 调整图的大小为10x8
sns.heatmap(a, vmin=-1, vmax=1, annot=True, fmt=".2f", cmap="coolwarm", annot_kws={"size": 12, "color": "red"})
plt.show()
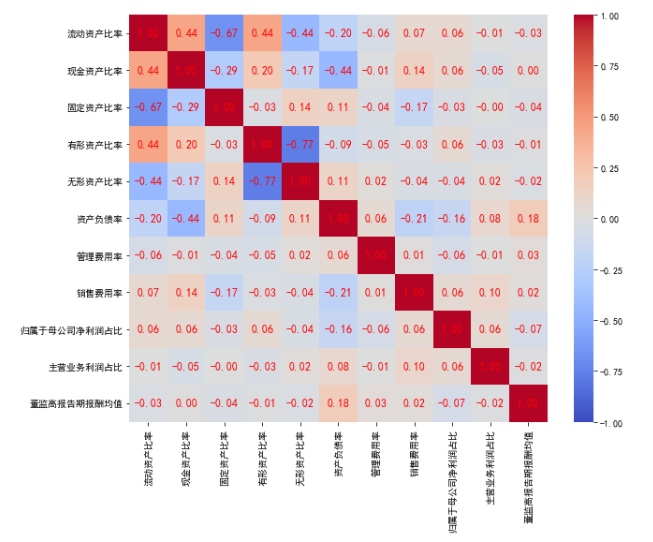
从解释变量之间的相关性分析可以看出:解释变量中(正/负)高相关性的变量需要从解释变量剔除
- “有形资产比率”与“无形资产比率”的相关系数为-0.77,考虑保留“无形资产比率”,同时删除“有形资产比率”
- “流动资产比率”与“固定资产比率”的相关系数为-0.67,考虑保留“流动形资产比率”,同时删除“固定资产比率”
xVars =['流动资产比率', '现金资产比率', '无形资产比率','资产负债率', '管理费用率', '销售费用率', '归属于母公司净利润占比', '主营业务利润占比', '董监高报告期报酬均值']
xd = data1[xVars]
xdcons = sma.add_constant(xd)
yd = data1[yVar]
# 参数估计
model = sma.OLS(yd, xdcons).fit()
model.summary2().tables[1]
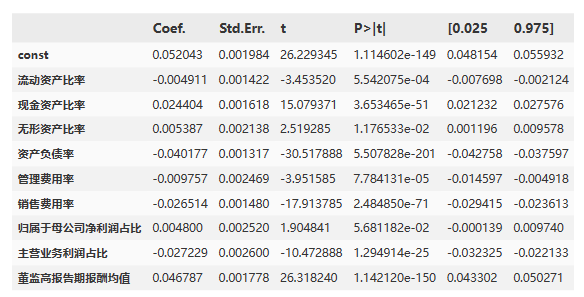
根据给出的回归系数和统计显著性水平,对每个解释变量进行分析:
-
流动资产比率(Coefficient: -0.004911, P-value: 0.000554):流动资产比率的增加与因变量的减少呈负相关关系,且统计上显著。
-
现金资产比率(Coefficient: 0.024404, P-value: 3.653465e-51):现金资产比率的增加与因变量的增加呈正相关关系,且统计上显著。
-
无形资产比率(Coefficient: 0.005387, P-value: 0.011765):无形资产比率的增加与因变量的增加呈正相关关系,但统计上显著性较低。
-
资产负债率(Coefficient: -0.040177, P-value: 5.507828e-201):资产负债率的增加与因变量的减少呈负相关关系,且统计上显著。
-
管理费用率(Coefficient: -0.009757, P-value: 7.784131e-05):管理费用率的增加与因变量的减少呈负相关关系,且统计上显著。
-
销售费用率(Coefficient: -0.026514, P-value: 2.484850e-71):销售费用率的增加与因变量的减少呈负相关关系,且统计上显著。
-
归属于母公司净利润占比(Coefficient: 0.004800, P-value: 0.056812):归属于母公司净利润占比的增加与因变量的增加呈正相关关系,但统计上显著性较低。
-
主营业务利润占比(Coefficient: -0.027229, P-value: 1.294914e-25):主营业务利润占比的增加与因变量的减少呈负相关关系,且统计上显著。
-
董监高报告期报酬均值(Coefficient: 0.046787, P-value: 1.142120e-150):董监高报告期报酬均值的增加与因变量的增加呈正相关关系,且统计上显著。
-
结论:流动资产比率、资产负债率、管理费用率、销售费用率和主营业务利润占比对因变量有显著影响,而现金资产比率、无形资产比率、归属于母公司净利润占比和董监高报告期报酬均值对因变量的影响可能较弱。
model.summary()
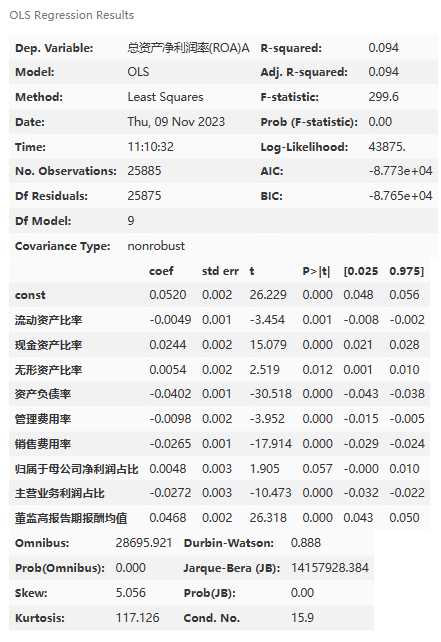
6、逐步加入关键解释变量
# 需要逐步加入的变量
xStepVars = ['流动资产比率', '现金资产比率', '无形资产比率', '管理费用率', '销售费用率', '归属于母公司净利润占比', '主营业务利润占比', '董监高报告期报酬均值']# 始终保留的变量(控制变量)
x0Vars = ['资产负债率']sts = ['Coef.', 'Std.Err.', 'P>|t|']
dst = ['Adj.$R^2$', 'AIC', 'BIC','Log-Likelihood']
step_res = pd.DataFrame(columns = pd.MultiIndex.from_product([xStepVars + ['整体回归'], sts]), # 最后加上一列,全部变量的整体回归index = xVars + dst )
for xsv in xStepVars:xns = [xsv] + x0Varsres = sma.OLS(yd, xdcons[xns]).fit()t_res = res.summary2().tables[1]t_res = t_res[sts]step_res[xsv] = t_res# 取出诊断统计量,放在 Coef. 列t_res = res.summary2().tables[0] for i in range(len(dst)):step_res[xsv, 'Coef.'][dst[i]] = t_res.iloc[i,3]# print(dst[i], ' = ', t_res.iloc[i + 1,3], '填充后 ', step_res[xsv, 'Coef.'][dst[i]])# 全部变量的整体回归结果
res = sma.OLS(yd, xdcons[xStepVars + x0Vars]).fit()
t_res = res.summary2().tables[1] # 取出系数估计结果
step_res['整体回归'] = t_res[sts] # 自动按照 index 匹配赋值# 取出诊断统计量,放在 Coef. 列
t_res = res.summary2().tables[0]
for i in range(len(dst)):step_res['整体回归', 'Coef.'][dst[i]] = t_res.iloc[i,3]
step_res
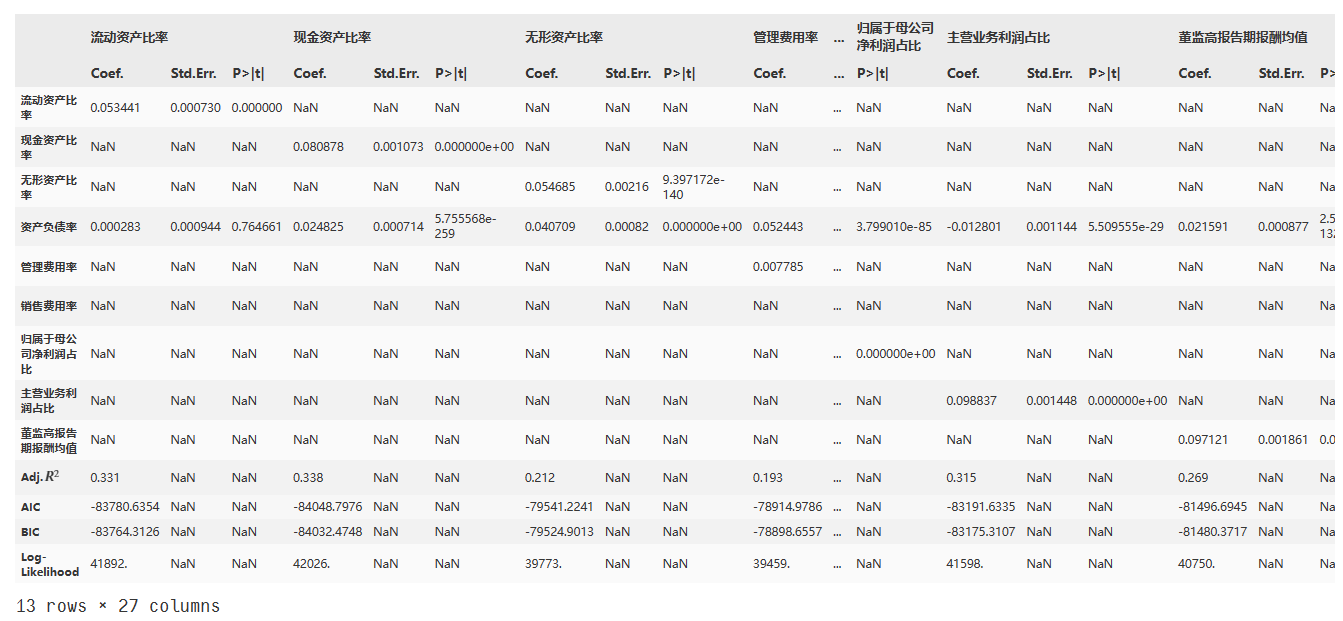
7、制作显著性表格
# 制作显著性表格
df = step_res
rows = df.indexdfres = pd.DataFrame(index = rows, columns = xStepVars + ['整体回归'])for xsv in xStepVars + ['整体回归']:coef = df[xsv].astype(float)['Coef.'].map(lambda x: '' if np.isnan(x) else ('%.3f') % x )pvs = df[xsv]['P>|t|'].map(lambda x: '***' if x<=0.01 else '**' if x<=0.05 else '*' if x<=0.1 else '')dfres[xsv] = coef + pvs
dfres.loc['Adj.$R^2$',:] = dfres.loc['Adj.$R^2$',:].map(lambda x: '' if np.isnan(float(x)) else ('%.3f%%') % (float(x)*100) )
dfres
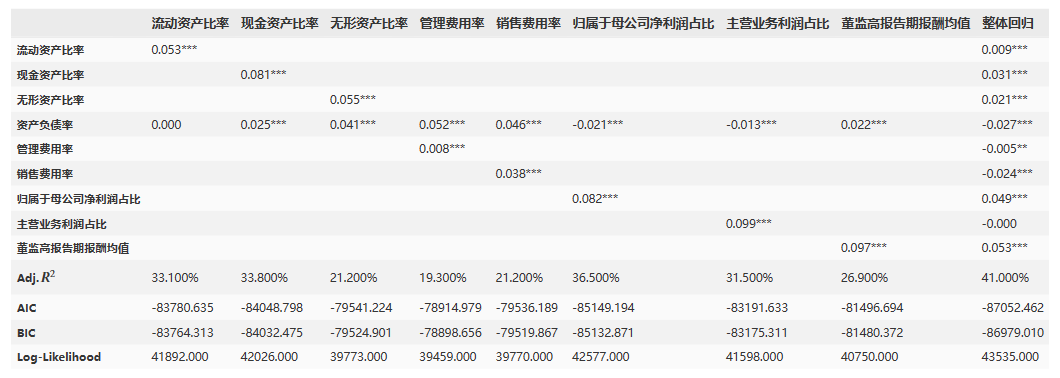
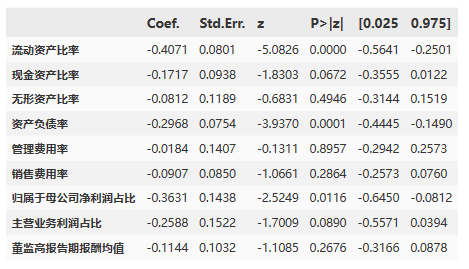
由上述显著性表格可知:
-
流动资产比率:流动资产比率与整体回归呈显著正相关。
-
现金资产比率:现金资产比率与整体回归呈显著正相关。
-
无形资产比率:无形资产比率与整体回归呈显著正相关。
-
资产负债率:资产负债率与整体回归呈显著负相关。
-
管理费用率:管理费用率与整体回归呈显著负相关。
-
销售费用率:销售费用率与整体回归呈显著负相关。
-
归属于母公司净利润占比:归属于母公司净利润占比与整体回归呈显著正相关。
-
主营业务利润占比:主营业务利润占比与整体回归呈显著正相关。
-
董监高报告期报酬均值:董监高报告期报酬均值与整体回归呈显著正相关。
8、经典logit回归
# 将因变量归一化
yd = MinMaxScaler().fit_transform(yd)
import statsmodels.api as sma# 将自变量和因变量赋值给Xbs和ybs
Xbs = xdcons[xStepVars + x0Vars]
ybs = yd# 为自变量添加常数列
Xbs_cons = sma.add_constant(Xbs)# 创建logit回归模型并拟合
lr = sma.Logit(ybs, Xbs_cons)
logit_res = lr.fit(method='lbfgs', maxiter=500)# 打印logit回归结果
logit_res.summary()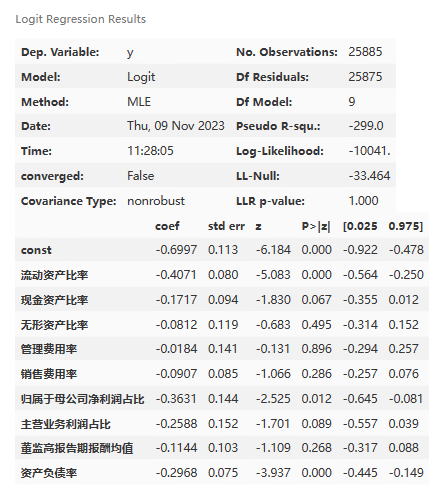
描述:
- No. Observations: 25885 - 观测样本的数量是25885。
- Model: Logit - 使用的模型是逻辑回归模型。
- Df Residuals: 25875 - 残差的自由度是25875。
- Method: MLE - 使用的估计方法是最大似然估计。
- Df Model: 9 - 模型的自由度是9,表示有9个自变量。
- Pseudo R-squ.: -299.0 - 伪R平方值为-299.0,表示模型拟合效果较差。 Time: 11:28:05 - 模型拟合的时间是上午11:28:05。
- Log-Likelihood: -10041. - 对数似然值为-10041.,表示模型的对数似然函数值。
- converged: False - 模型是否收敛,False表示模型未收敛。
- LL-Null: -33.464 - 空模型的对数似然值为-33.464。
- Covariance Type: nonrobust - 协方差类型为非鲁棒性。
- LLR p-value: 1.000 - 对数似然比检验的p值为1.000,表示模型的拟合效果不显著。
lr = sma.Logit(ybs, Xbs_cons)
# logit_res = lr.fit(method = 'lbfgs', maxiter = 500)
logit_res = lr.fit_regularized(method = 'l1', maxiter = 500, alpha = 1, trim_mode = 'size')
logit_res.summary()
res = logit_res.summary2().tables[1]
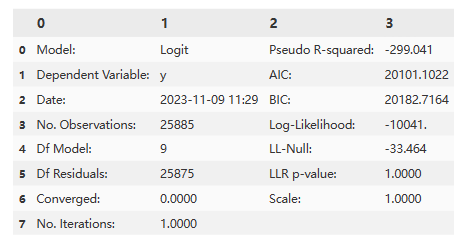
logit_res.summary2().tables[0]
round(res.loc[xVars,:],4)




)

)

)
)









