1.空间复杂度
空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用存储空间大小的量度 。
空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。 空间复杂度计算规则基本跟实践复杂度类似,也使用大O渐进表示法。
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。 实例1:
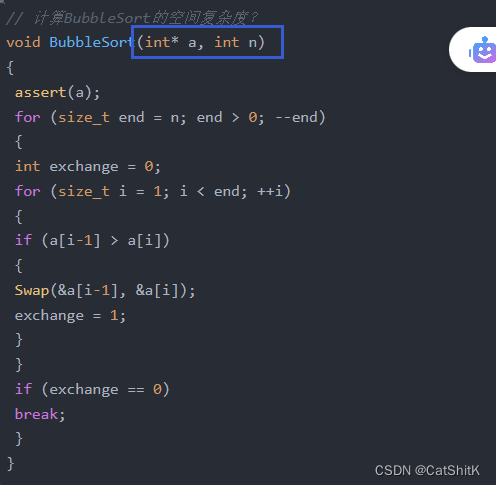
// 计算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
O(1)
我们理解空间复杂度就可以用这个函数为了完成这个功能所额外开辟的空间
因为是初始值,所以指针a和n不算是额外开辟的(必须要有他们才能开始执行函数)
而这三个就是额外创建的变量所以
O(3)->O(1)
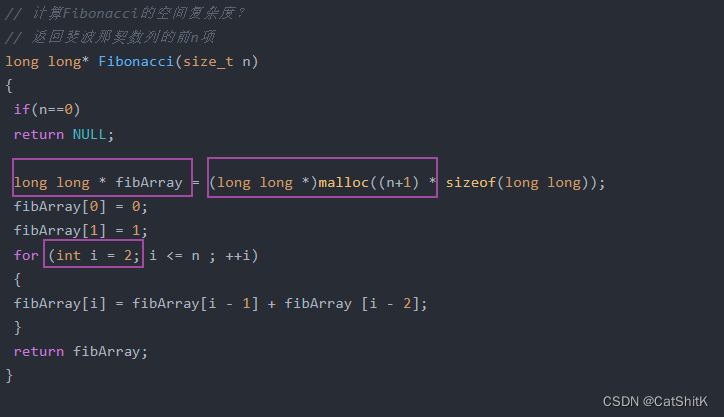
// 计算Fibonacci的空间复杂度?
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{if(n==0)return NULL;long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n ; ++i){fibArray[i] = fibArray[i - 1] + fibArray [i - 2];}return fibArray;
}O(n)
O(n+3)->O(n)
大多数空间复杂度为O(1)或O(n)
// 计算阶乘递归Fac的空间复杂度?
long long Fac(size_t N)
{if(N == 0)return 1;return Fac(N-1)*N;
}O(n)
因为函数栈帧也算是空间的开辟 而这里函数开辟了n块空间
如果用的是for循环,就只需要O(1)
// 计算斐波那契递归Fib的时间复杂度?
long long Fib(size_t N)
{if(N < 3)return 1;return Fib(N-1) + Fib(N-2);
}
O(n)
简单理解就是调用递归函数时,会先从下图的紫框的顺序向下调用函数,而调用这些函数的同时,在函数右边的的还会使用同一块空间,所以,真正开辟的空间是O(n),调用完函数后就会销毁,所以不是累加O(n^2)
2. 常见复杂度对比
一般算法常见的复杂度如下:
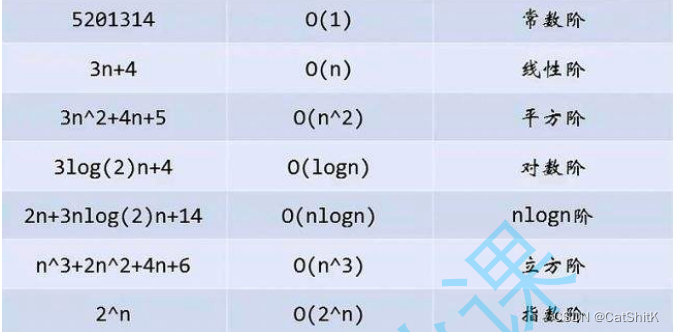
3.进阶题目练习
189. 轮转数组 - 力扣(LeetCode)
给定一个整数数组
nums,将数组中的元素向右轮转k个位置,其中k是非负数。示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3 输出:[5,6,7,1,2,3,4]解释: 向右轮转 1 步:[7,1,2,3,4,5,6]向右轮转 2 步:[6,7,1,2,3,4,5]向右轮转 3 步:[5,6,7,1,2,3,4]示例 2:
输入:nums = [-1,-100,3,99], k = 2 输出:[3,99,-1,-100] 解释: 向右轮转 1 步: [99,-1,-100,3] 向右轮转 2 步: [3,99,-1,-100]提示:
1 <= nums.length <= 105-231 <= nums[i] <= 231 - 10 <= k <= 105
3.1 方法一(暴力求解)
通过暴力求解直接将数组最后一位保存在tmp里,前面的数组向后移动1位,循环k次
方法直接但是时间复杂度不符合要求,最差的情况是要交换n-1次,当k=n时数组旋转不变。

3.2 方法二(牺牲空间换时间)

我们翻转后可以得到规律:当我们轮转3次,,前4个数组(7-3)移动到了后面,而后三个数组(k)移动到了前面,我们就可以拷贝数组到一个新的数组里去。再把他拷贝回去

实现:
void rotate(int* nums, int numsSize, int k) {int* tmp = (int*)malloc(sizeof(int) * numsSize); //创建新的数组int n = numsSize; //存放n的值好进行运算k%= n; //旋转次数等于数组大小等于没有旋转memcpy(tmp, nums + n - k, sizeof(int) * k); //后n-k=4的值存放在tmp前面memcpy(tmp+k, nums, sizeof(int) * (n-k)); //前k=3的值存放在tmp(n-k)=4的位置memcpy(nums, tmp, sizeof(int) * n); //拷贝回去覆盖3.3 方法三(前交换,后交换,整体交换)
找规律,正常情况不容易想出来
void reveune(int* a, int left, int right)
{while (left < right){int tmp = a[left];a[left] = a[right];a[right] = tmp;left++;right--;}}void rotate(int* nums, int numsSize, int k)
{int n = numsSize;k %= n;reveune(nums, 0, n - k-1);reveune(nums, n-k, n-1);reveune(nums, 0, n-1 );
}

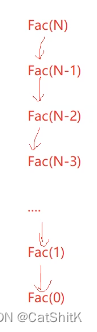




主副控智能自动断电桌面PDU插排)






)






/阻塞队列)

)
