17-Java语言概述-Java语言的特点和JVM的功能_哔哩哔哩_bilibili
1.java优点
跨平台性
在jvm上运行
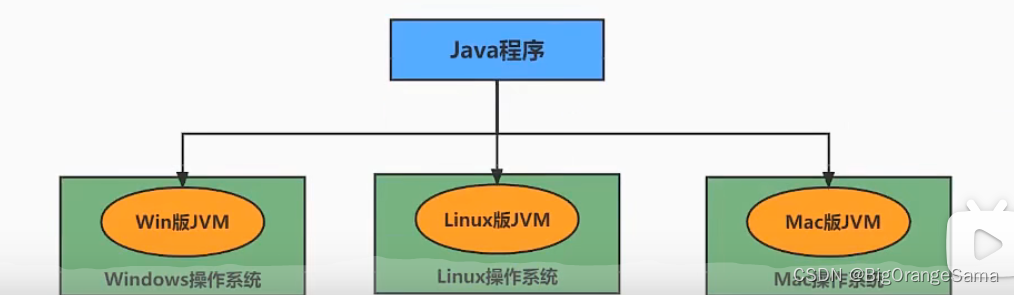
2.jvm
2.1实现跨平台性
不需要对每一种指令集编写编译器，只需要针对jvm编程，jvm会自动转换
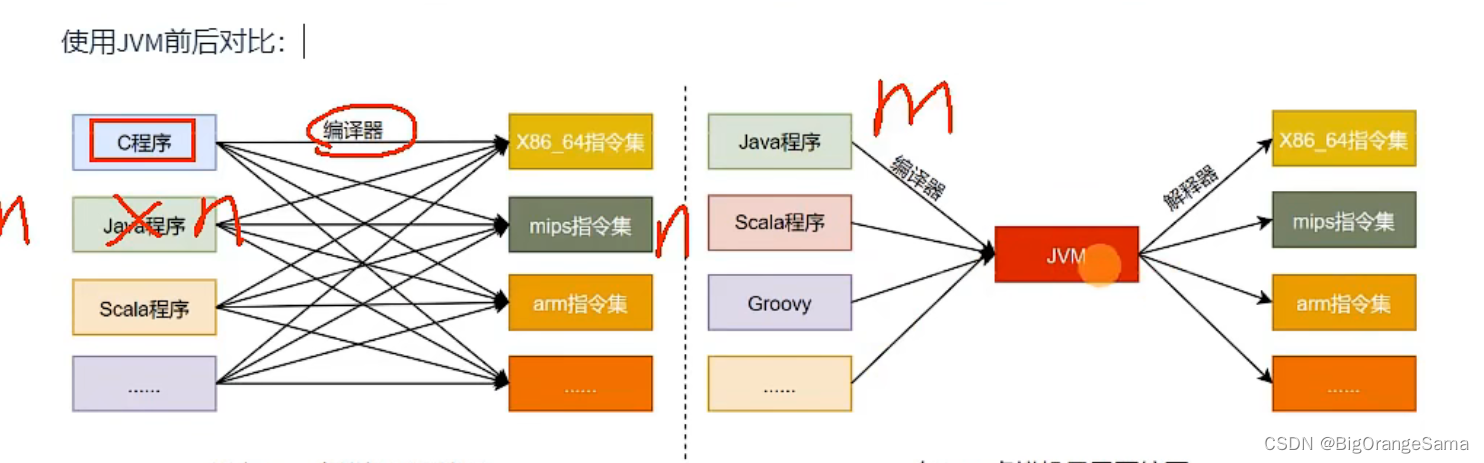
2.2内存回收
内存溢出：用的内存太多已经占满了，且都不是垃圾无法回收，那么新申请内存就会溢出
内存泄露：以为回收了内存，但实际没有，导致一块内存一直没法使用
3.后续安排
4.一些术语
JDK、JRE、JVM三者之间的关系：前者包含后者
5.一些常见问题
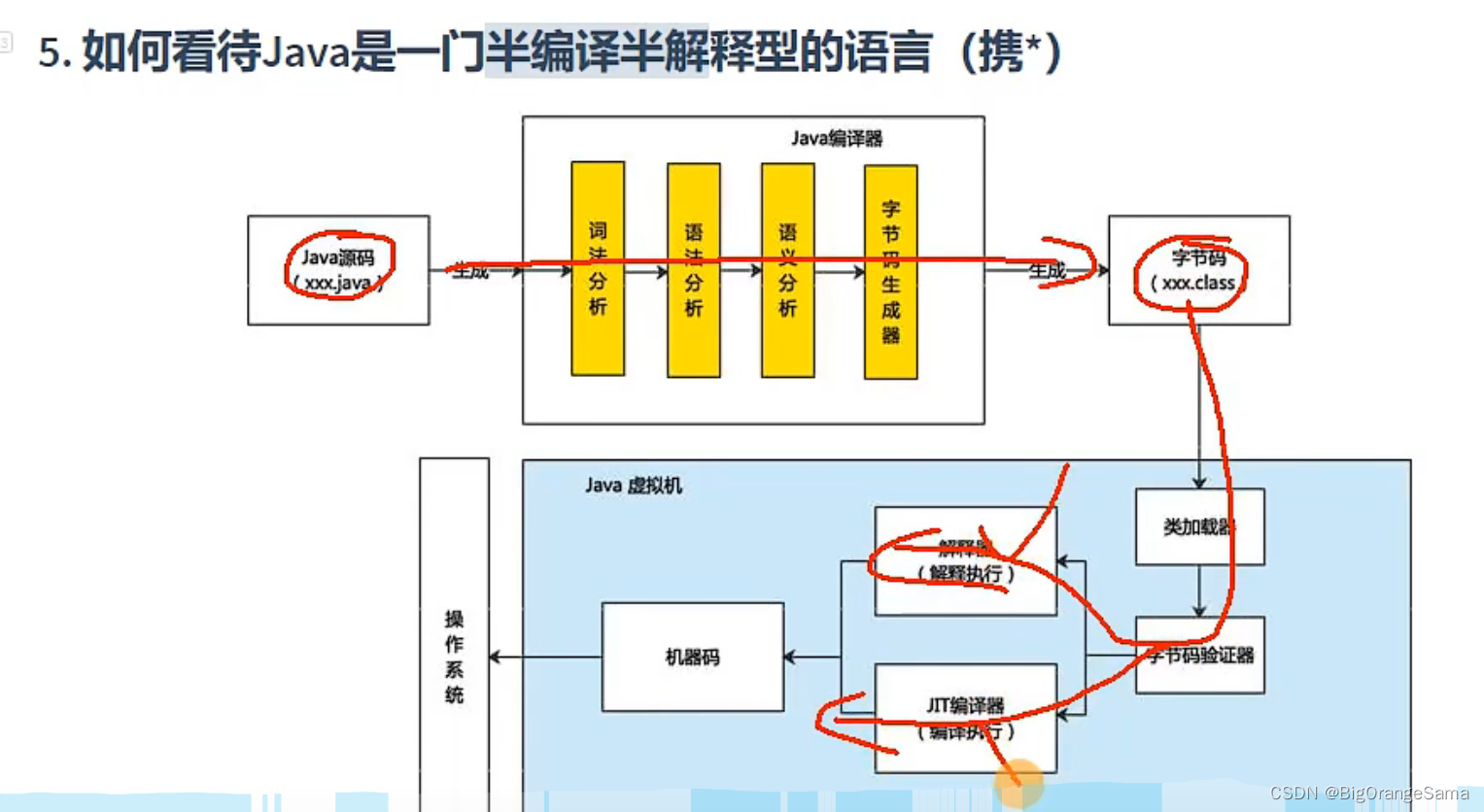
先编译成字节码，然后在jvm中，可能走解释器也可能走JIT编译器
)
