41题

41题解答：

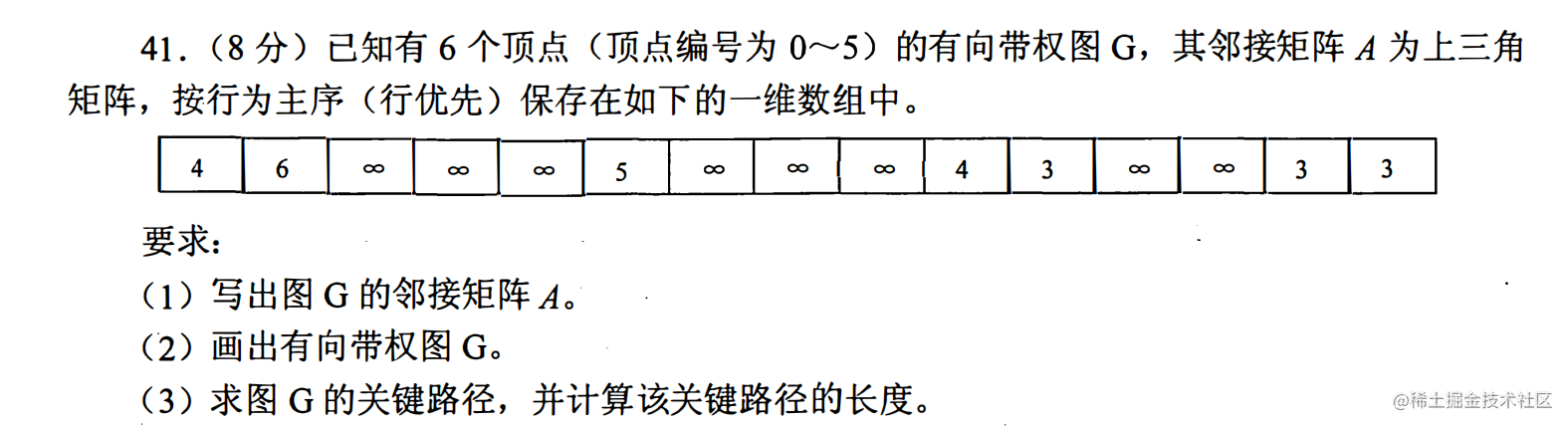
（1）图 G 的邻接矩阵 A 如下所示：

由题意得，A为上三角矩阵，在上三角矩阵A[6][6]中，第1行至第5行主对角线上方的元素个数分别为5, 4, 3, 2, 1

用 “ 平移” 的思想，将题目中前5个、后4个、后3个、后2个、后1个元素，分别移动到矩阵对角线 (“O”) 右边的行上,可得下图

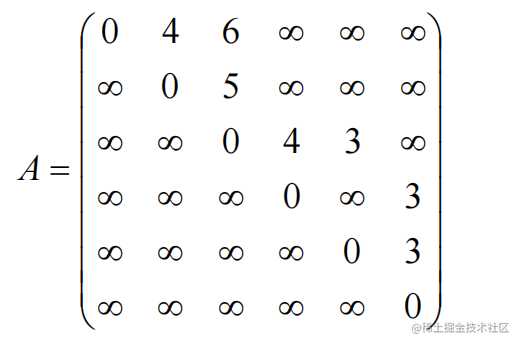
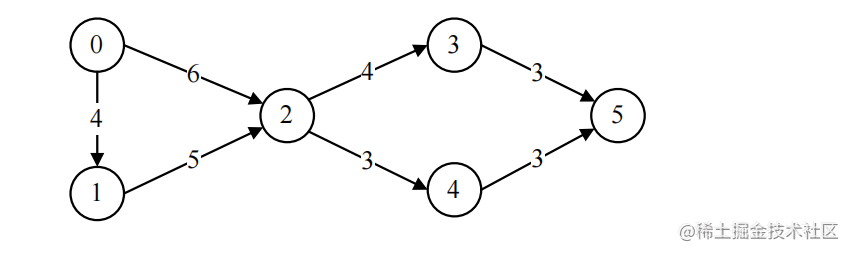
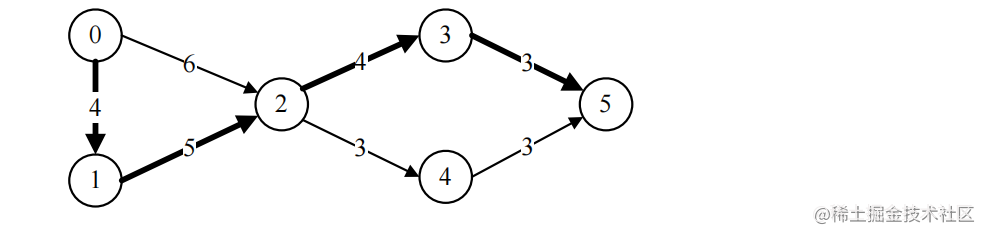
（2）根据上面的邻接矩阵，画出有向带权图G

（3）按照算法，先计算各个事件的最早发生时间，计算过程如下：

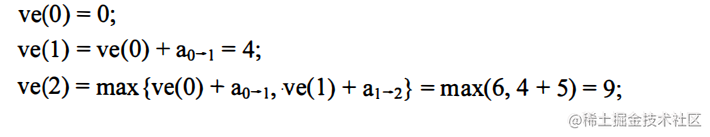
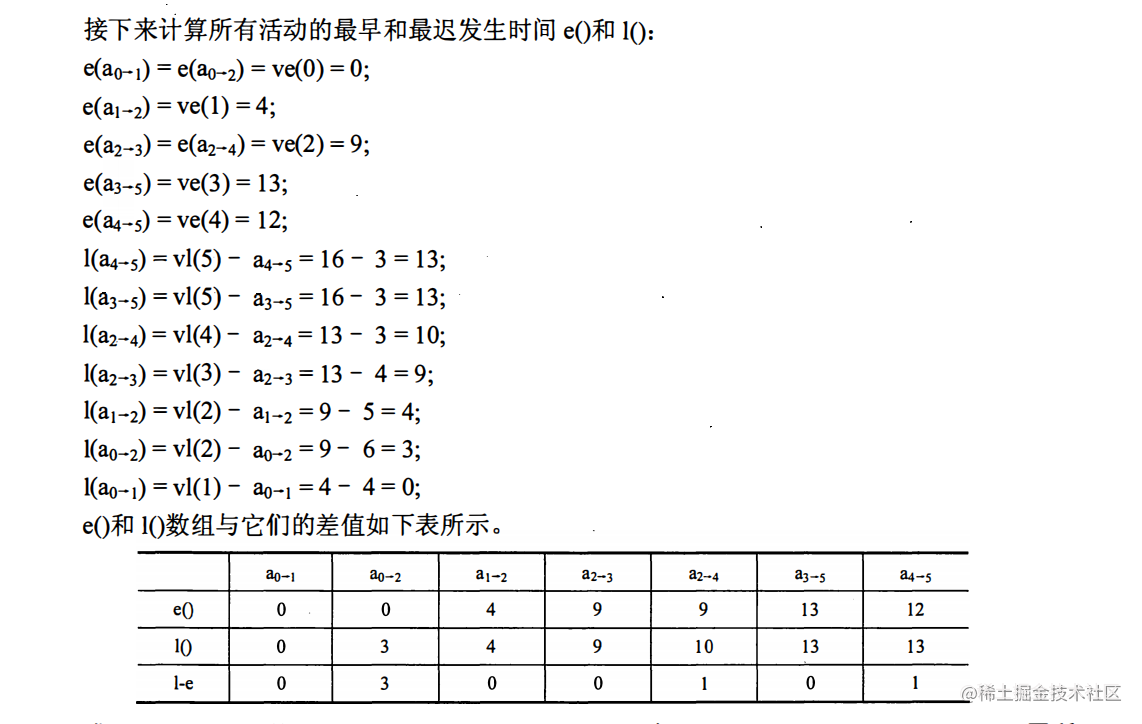
关键路径为 0->1->2->3->5（如下图所示粗线表示），长度为 4+5+4+3=16。

---

42题

暴力解1：将两个数组合并成一个，然后找中位数即可

int merge(Sqlist A,Sqlist B) {int i=0,j=0,count=0;while(1){if(A.data[i]<B.data[i]){if(++count==(A.length+B.length)/2){return A.data[i];}++i;}else{if(++count==(A.length+B.length)/2){return B.data[i];}++j;}}
}

暴力解2：

• 新建一个数组C
• 合并到数组C
• 排序

---

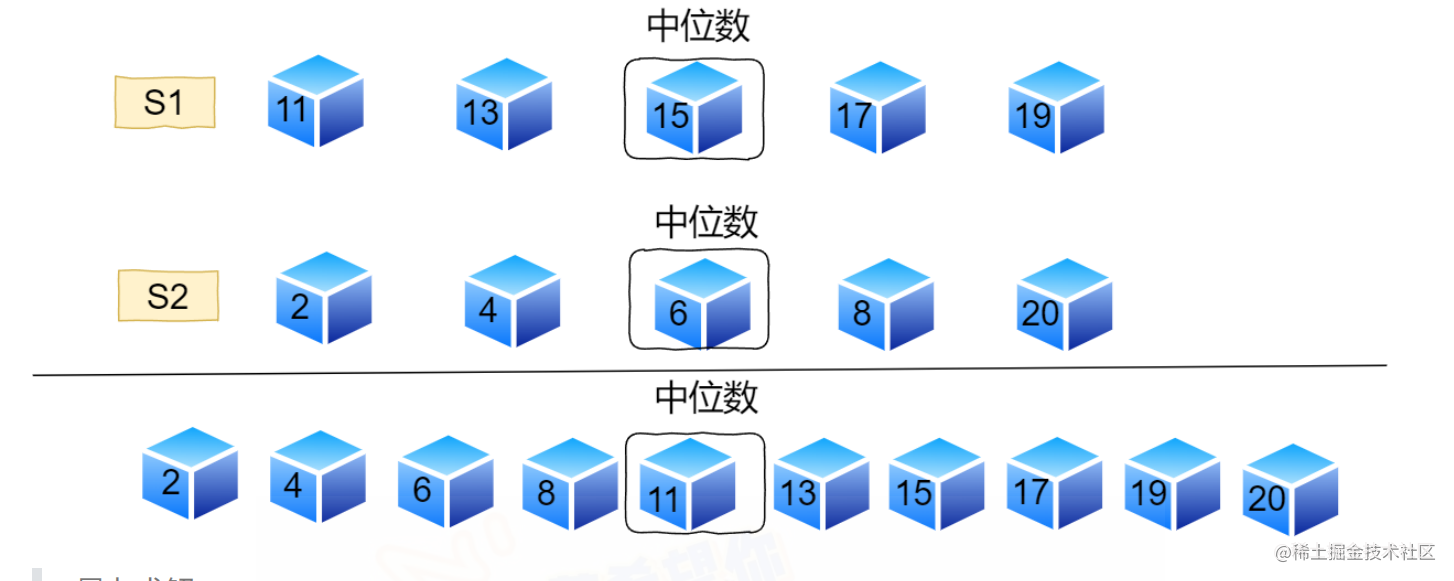
• 要求找到两个等长有序序列合并后的中位数，暴力解就直接合并
• 但你会发现并不需要合并全部，我们只需要中间位置的一个值即可
• 所以 mid 就是 len-1，我们按照常规合并有序序列的方法，只移动指针即可

int serach_mid(int A[], int B[], int len) {int i = 0, j = 0;while (i + j < len - 1) {if (A[i] <= B[j]) {i++;} else {j++;}return A[i] <= B[j] ? A[i] : B[j];}
}

最优解：

思路:

1）求两个序列A和B的中位数最简单的办法就是将两个升序序列进行归并排序，然后求其中位数。这种解法虽可求解，但在时间和空间两方面都不大符合高效的要求，但也能获得部分分值。

根据题目分析，分别求两个升序序列A和B的中位数，设为a和b。

① 若a=b，则a或b即为所求的中位数。

原因：容易验证，如果将两个序列归并排序，则最终序列中，排在子序列ab前边的元素为先前两个序列中排在a和b前边的元素；排在子序列ab后边的元素为先前两个序列中排在a和b后边的元素。所以子序列ab一定位于最终序列的中间，又因为a=b，显然a就是中位数。

② 否则（假设a<b），中位数只能出现（a，b）范围内。

原因：同样可以用归并排序后的序列来验证，归并排序后必然有形如…a…b…的序列出现，中位数必出现在（a，b）之间。因此可以做如下处理：舍弃a所在序列A的较小一半，同时舍弃b所在序列B的较大一半。在保留两个升序序列中求出新的中位数a和b，重复上述过程，直到两个序列中只含一个元素时为止，则较小者即为所求的中位数。每次总的元素个数变为原来的一半。

算法的基本设计思想如下。

分别求出序列A和B的中位数，设为a和b，求序列A和B的中位数过程如下：

① 若a=b，则a或b即为所求中位数，算法结束。

② 若a<b，则舍弃序列A中较小的一半，同时舍弃序列B中较大的一半，要求舍弃的长度相等。

③ 若a>b，则舍弃序列A中较大的一半，同时舍弃序列B中较小的一半，要求舍弃的长度相等。

在保留的两个升序序列中，重复过程①、②、③，直到两个序列中只含一个元素时为止，较小者即为所求的中位数。

int M_Search(int A[], int B[], int n) {int s1 = 0, d1 = n - 1, m1, s2 = 1, d2 = n - 1, m2;//分别表示序列A和B的首位数、末位数和中位数while (s1 != d1 || s2 != d2) {m1 = (s1 + d1) / 2;m2 = (s2 + d2) / 2;if (A[m1] == B[m2])return A[m1];           //满足条件1）if (A[m1] < B[m2]) {        //满足条件2）if ((s1 + d1) % 2 == 0) { //若元素个数为奇数s1 = m1;            //舍弃A中间点以前的部分，且保留中间点d2 = m2;            //舍弃B中间点以后的部分，且保留中间点} else {               //元素个数为偶数s1 = m1 + 1;          //舍弃A中间点及中间点以前部分d2 = m2;              //舍弃B中间点以后部分且保留中间点}} else {                     //满足条件3）if ((s1 + d1) % 2 == 0) { //若元素个数为奇数d1 = m1;            //舍弃A中间点以后的部分，且保留中间点s2 = m2;            //舍弃B中间点以前的部分，且保留中间点}else {                 //元素个数为偶数d1 = m1 + 1;          //舍弃A中间点以后部分，且保留中间点s2 = m2;              //舍弃B中间点及中间点以前部分}}}return A[s1] < B[s2] ? A[s1] : B[s2];
}