目录
串行传输和并行传输
同步传输和异步传输
单工、半双工和全双工通信
串行传输和并行传输
串行传输是指数据是一个比特一个比特依次发送的。因此在发送端和接收端之间,只需要一条数据传输线路即可。

并行传输是指一次发送n个比特,而不是一个比特,为此在发送端和接收端之间,需要有n条传输线路。
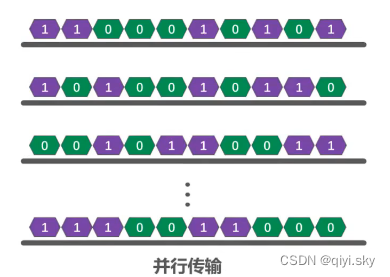
并行传输的优点是:速度为串行传输的n倍;但也存在一个严重的缺点,即成本高 。
在计算机网络中,数据在传输线路上的传输采用的是串行传输
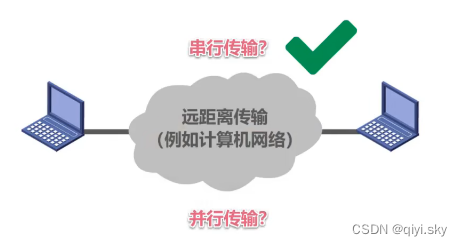
计算机内部的数据传输,常采用并行传输方式。例如CPU与内存之间,通过总线进行数据传输,常见的数据总线宽度有8位16位,32位和64位 。

同步传输和异步传输
再来看同步传输和异步传输,
采用同步传输方式,数据块以稳定的比特流的形式传输,字节之间没有间隔。

接收端在每个比特信号的中间时刻进行检测,以判别接收到的是比特0还是比特1:

由于不同设备的时钟频率存在一定差异,不可能做到完全相同。所以在传输大量数据的过程中,所产生的判别时刻的累积误差会导致接收端对比特信号的判别错位。

因此需要采取方法,使收发双方的时钟保持同步,实现收发双方时钟同步的方法主要有两种:
一种是外同步,也就是在收发双方之间添加一条单独的时钟信号线,发送端在发送数据信号的同时,另外发送一路时钟同步信号,接收端按照时钟同步信号的节奏,来接收数据。
另一种是内同步,也就是发送端将时钟同步信号编码到发送数据中一起传输,例如传统以太网所采用的就是曼彻斯特编码,这部分内容我们将在以后详细讨论。

采用异步传输方式时,以字节为独立的传输单位。

字节之间的时间间隔不是固定的,接收端仅在每个字节的起始处对字节内的比特实现同步。为此通常要在每个字节前后,分别加上起始位和结束位。

这里异步是指字节之间异步,也就是字节之间的时间间隔不固定,但字节中的每个比特仍然要同步,也就是各比特的持续时间是相同的。

单工、半双工和全双工通信
再来看单工、半双工和全双工,
单工通信又称为单向通信,通信双方只有一个数据传输方向。
例如:无线电广播采用的就是这种通信方式:

半双工又称为双向交替通信,通信双方可以相互传输数据,但不能同时进行。
例如:对讲机采用的就是这种通信方式:

全双工通信又称为双向同时通信,通信双方可以同时发送和接收信息
例如:电话采用的就是这种通信方式 :

单向通信只需要一条信道,而双向交替通信或双向同时通信,则都需要两条信道(每个方向各一条)。
END
学习自:湖科大——计算机网络微课堂



)


2016c语言题)












,模糊清晰、划痕修复及黑白上色的实践)