什么是栈?
一种特殊的线性表,只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶,另一端称为栈底。栈中的数据元素遵守后进先出(LIFO - Last In First Out)的原则。
从数据结构的角度来看,栈 就是一种数据结构。
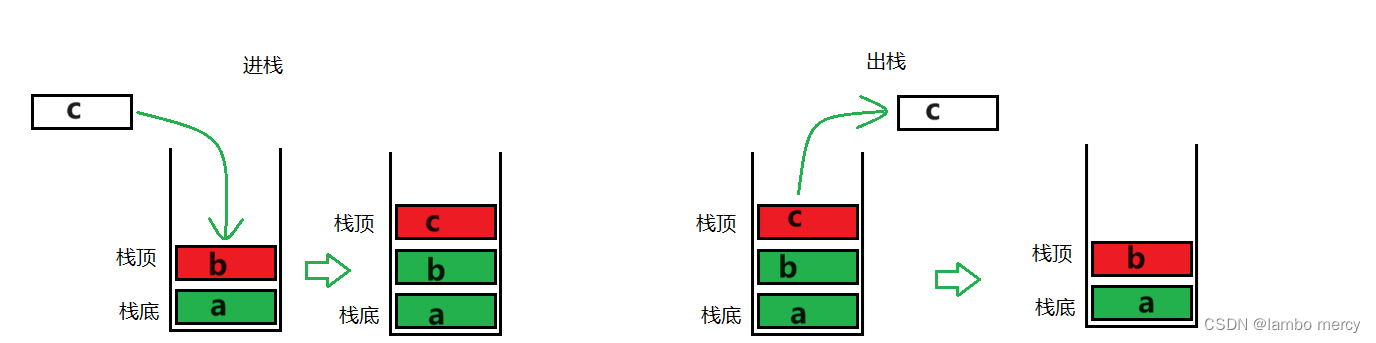
压栈 和 出栈
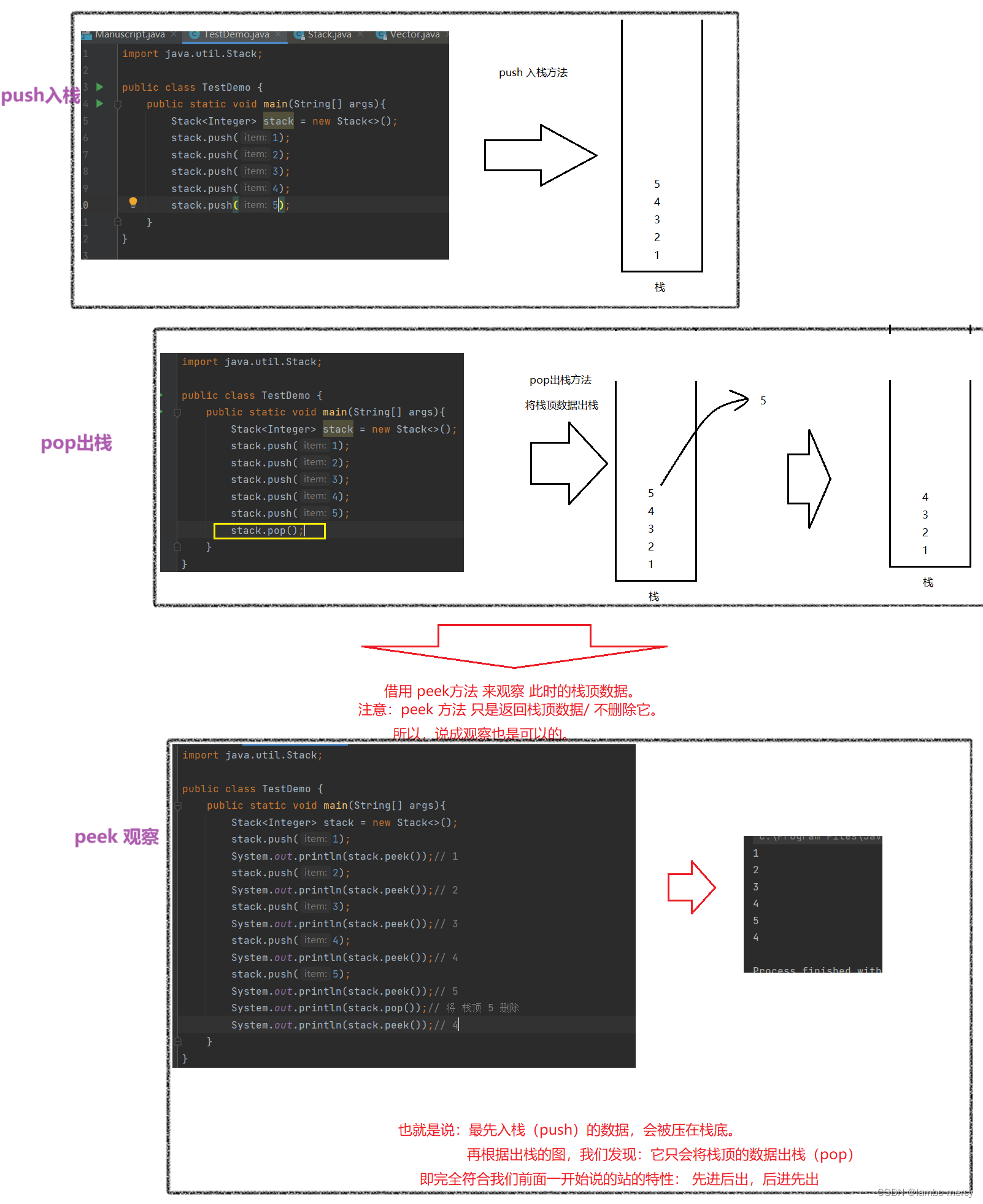
- 压栈:栈的插入操作叫做进栈/压栈/入栈,入数据在栈顶。
- 出栈:栈的删除操作叫做出栈。出数据在栈顶。
Java 虚拟机栈
Java 虚拟机 JVM 可分五个部分
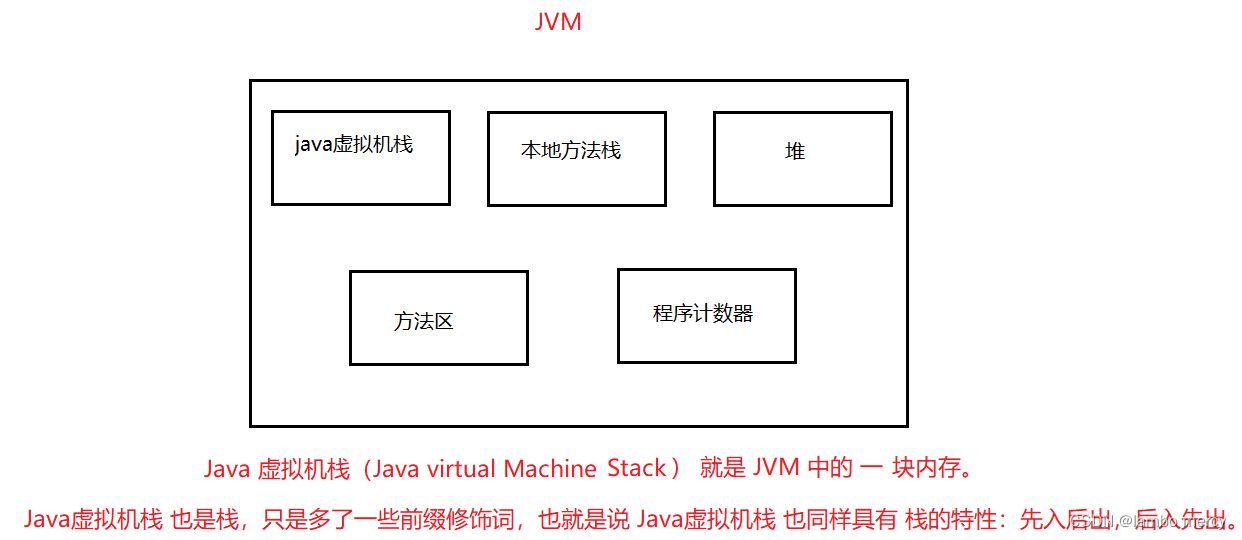
方法区:存放类定义信息、字节码、常量等数据,在Sun HotSpot JVM中,这块也称为Perm Gen。
堆:创建的对象信息将放入堆中,堆内部如何实现各虚拟机各不相同,对于Sun HotSpot JVM来说又分为Young Gen和Tenured Gen,更详细描述参见《[Java性能剖析]Sun JVM内存管理和垃圾回收 》
Java栈:对于每个执行线程,会分配一个Java栈,JVM在执行过程当中,每执行一个方法,都会为方法在当前栈中增加一个栈帧,每个栈帧的信息与具体实现相关,但一般会由3部分组成:变量区,方法参数和本地变量会放入这个位置,大小是固定的,在进行方法时会先分配好,在类定义中,会由max local来指定这块区的大小;方法信息区,会包括当前类常量池的入口地址等信息,这块大小也是固定的;操作栈,与Intel体系架构中的运算使用寄存器来进行不一样,JVM的字节码的方法调用、运算等需要的参数,都是通过操作栈来传递的。在类定义中,会由max stack指定最大的操作栈。关于Java栈的更详细描述参见《Java 栈内存介绍 》
本地方法栈:对本地方法的调用,并不会使用Java栈而是使用本地方法栈,本地方法栈的组成取决于所使用的平台和操作系统.
PC寄存器/程序计数器:对于每个执行线程会分配一个PC寄存器,寄存器中存放当前字节码的执行位置
栈帧
在调用函数的时候,我们会为这个函数在java虚拟机栈中开辟一块内存,叫做栈帧。

栈的使用
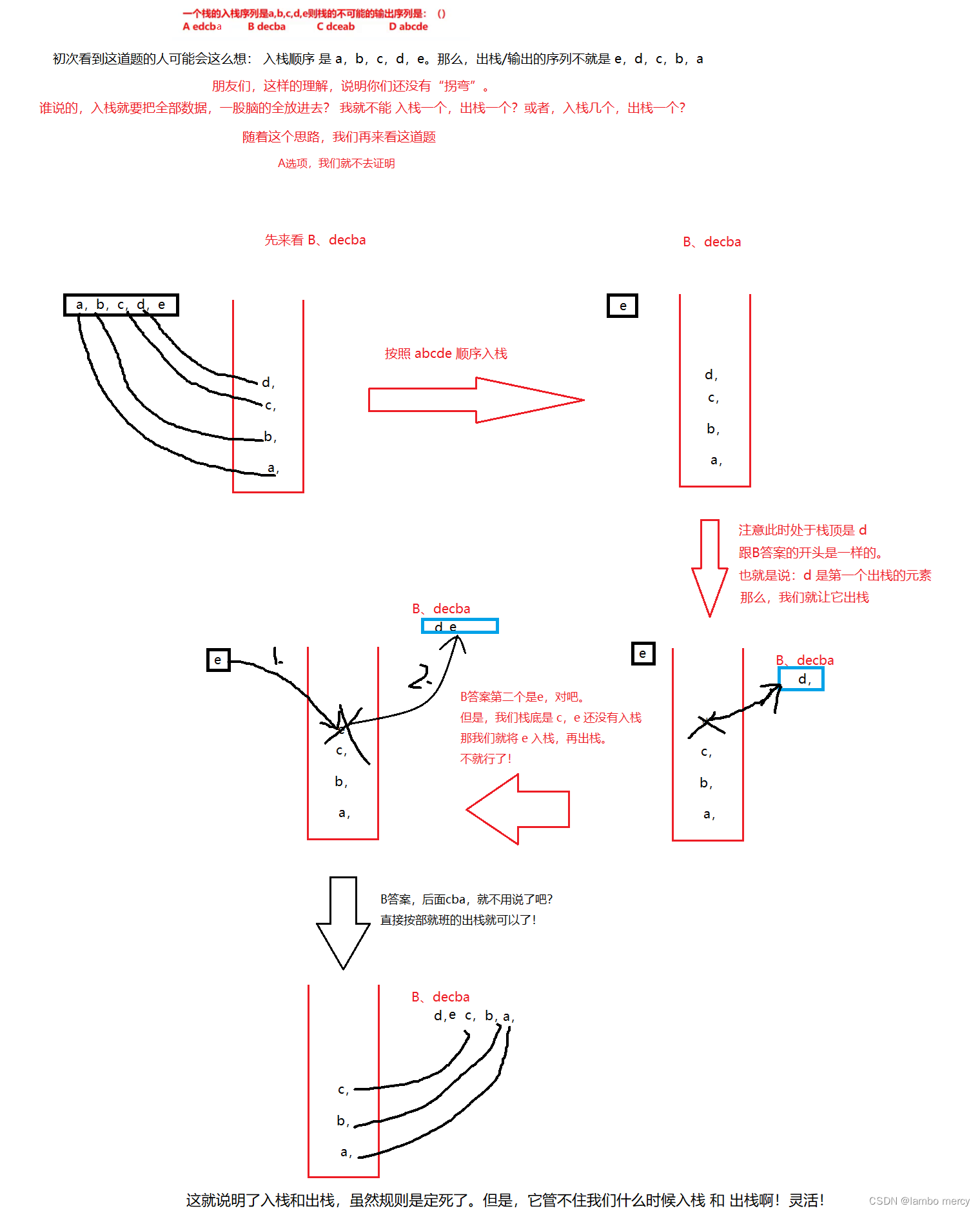
1.入栈 和 出栈的顺序
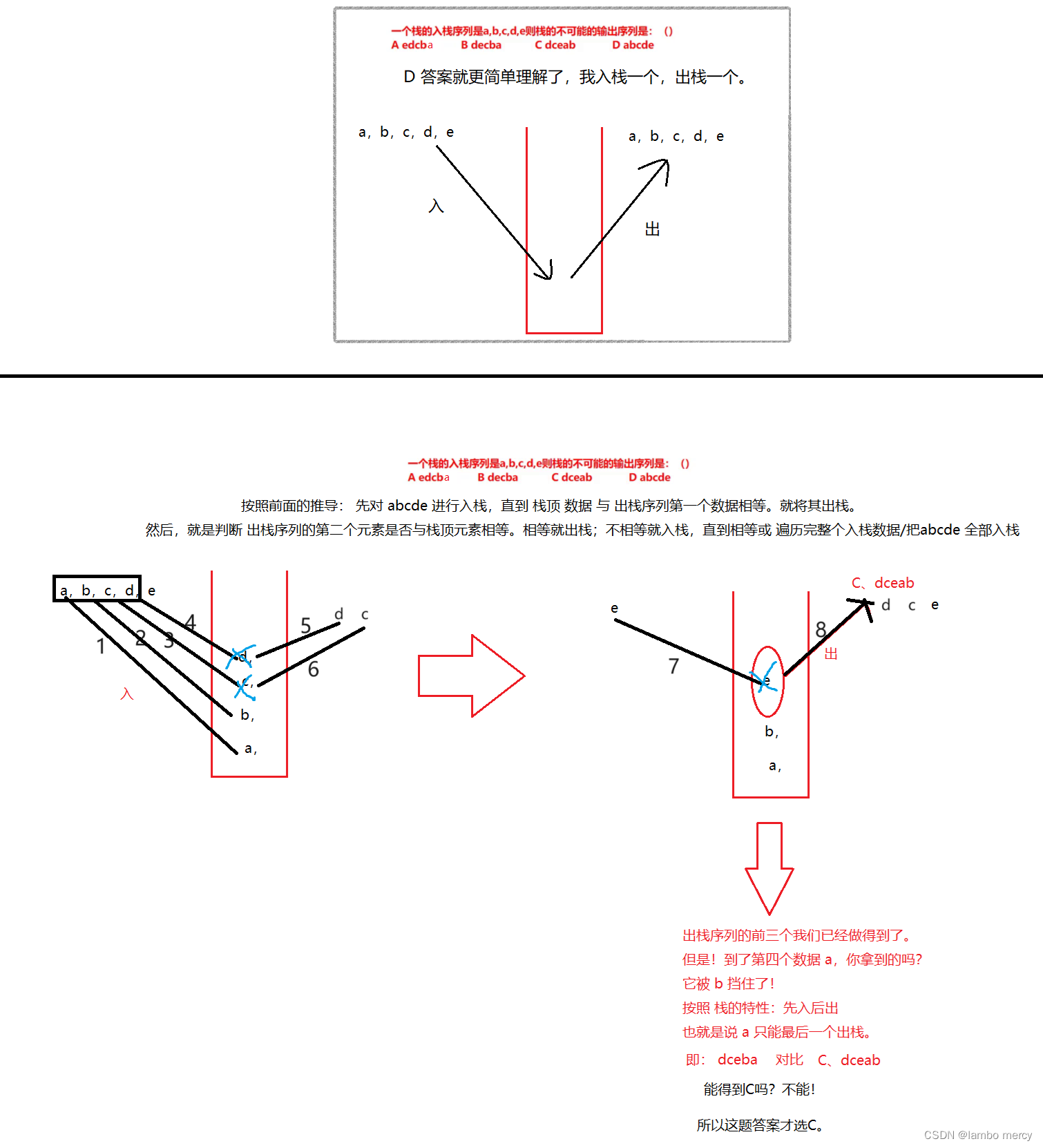
中缀 和 后缀 表达式的表现形式
中缀表达式:最常见的表达式,就是我们平常使用的: a + b、a - c、a * b、a/b。
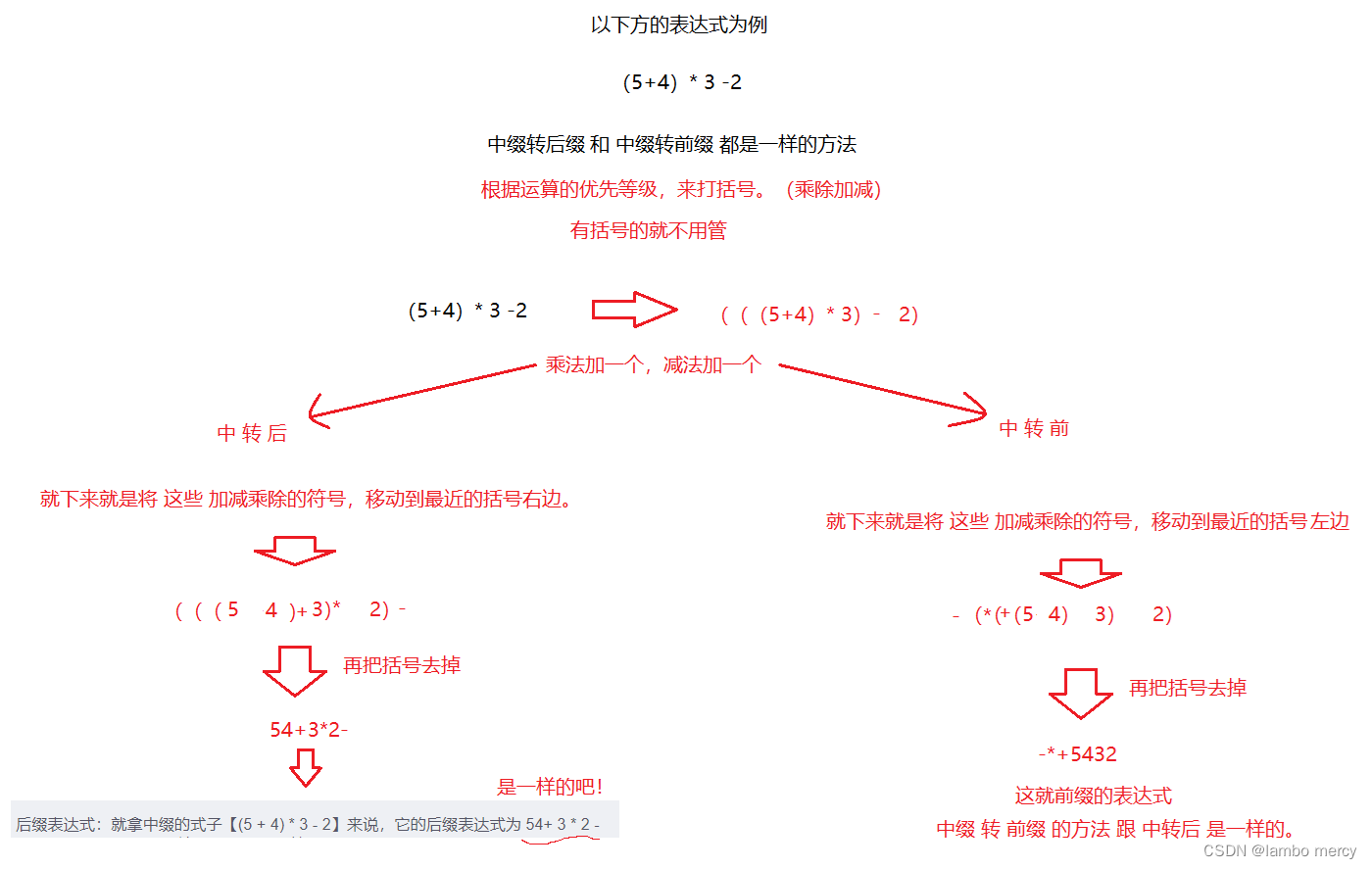
还可以加括号 (5 + 4) * 3 - 2。
后缀表达式:就拿中缀的式子【(5 + 4) * 3 - 2】来说,它的后缀表达式为 54+ 3 * 2 -
再来看一个 a + b * c ,这个中缀表达式转换成 后缀表达式为 abc*+
中缀转后缀 和 中缀转前缀 的方法
实战题
150. 逆波兰表达式求值 - 力扣(LeetCode)
解题思维
借助栈和循环,思维是这样的:
- 如果 i 下标的元素 是 数字,直接入栈。
- 如果 i 下标的元素 是 运算符时,出栈两个数字 进行运算,再将其计算结果入栈。
- 以此类推!
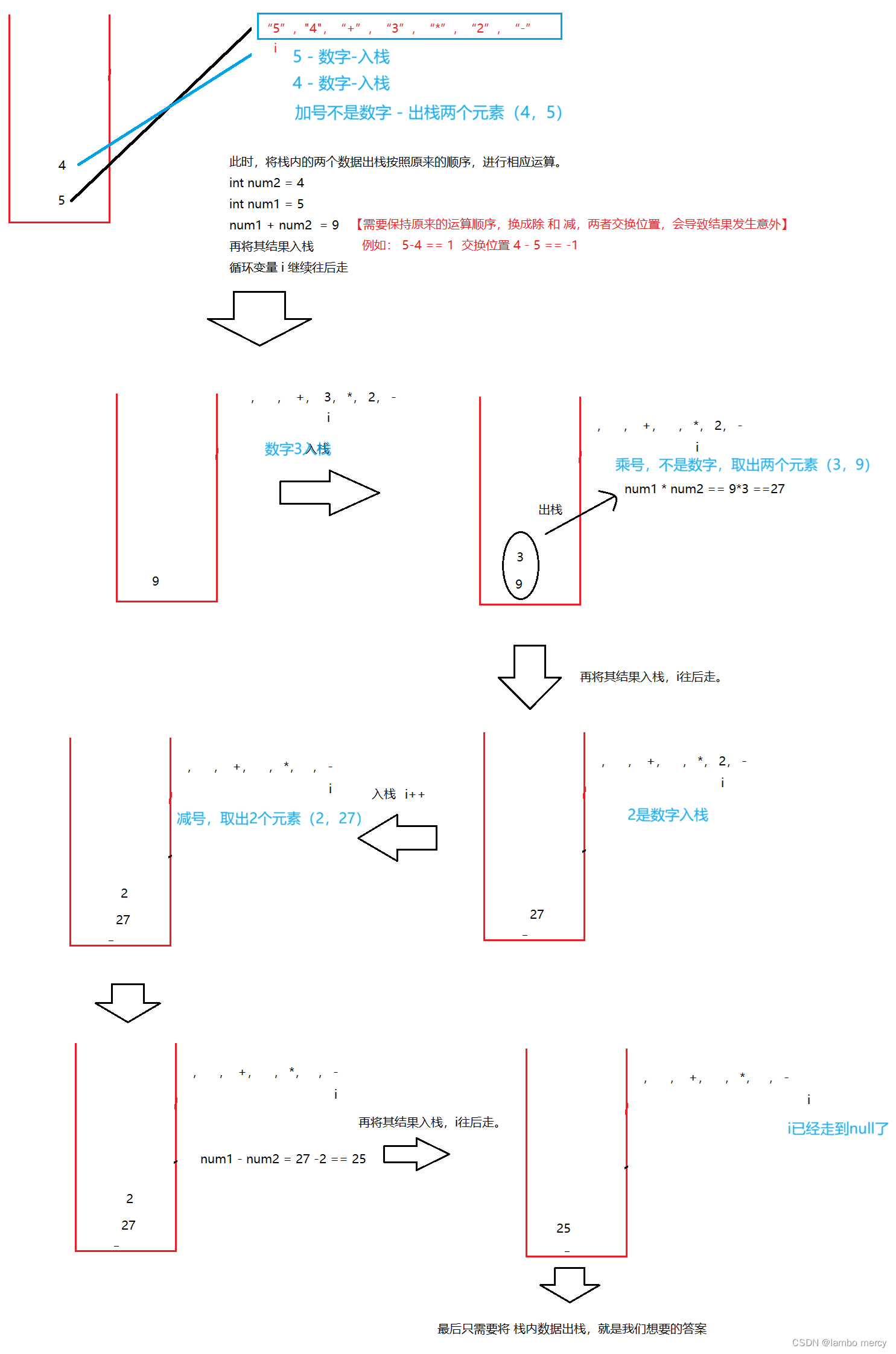
代码阶段:
1、怎么 new 一个 Stack

进入 栈Stack 类,按下 alt + 7
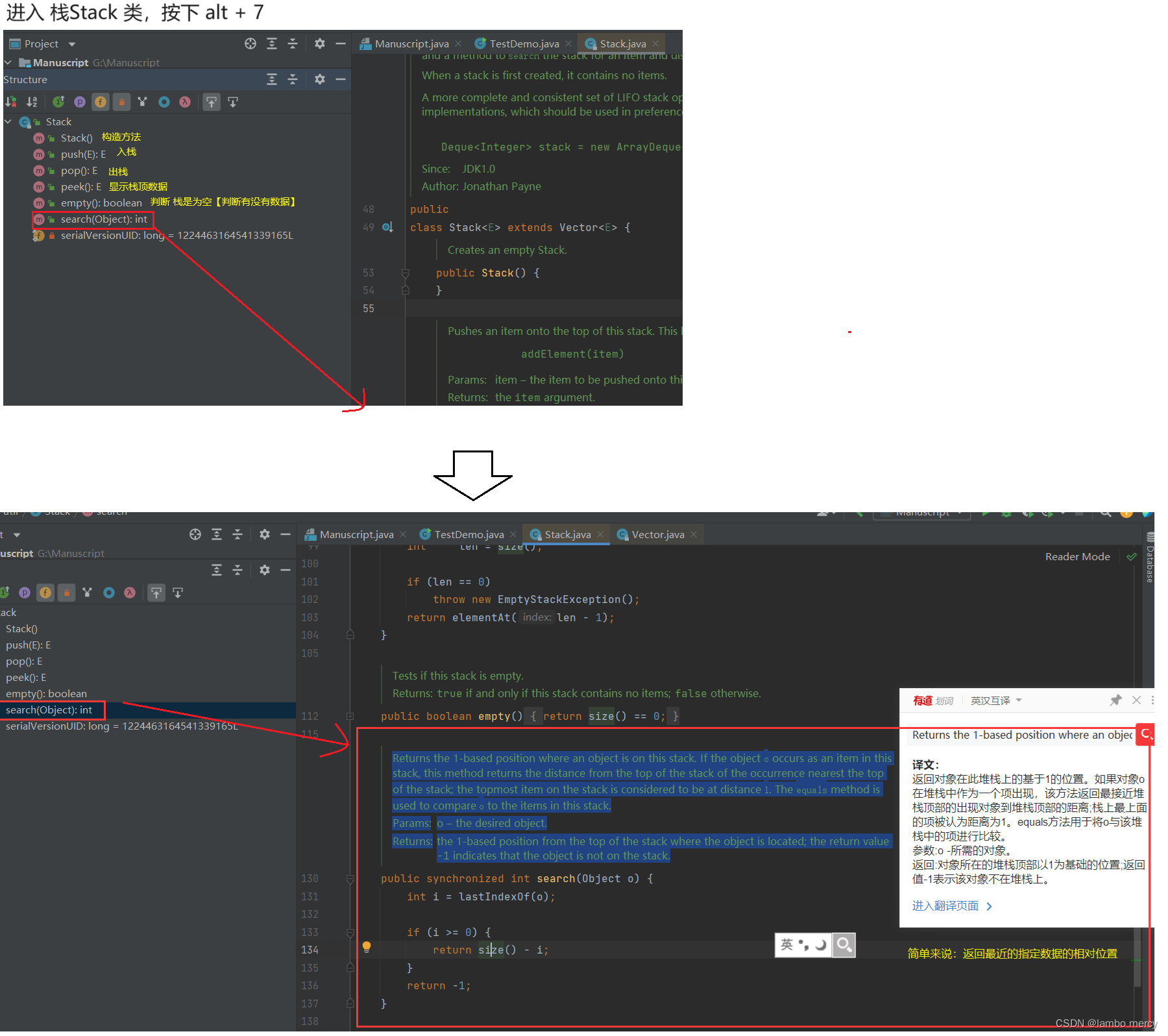
2、Stack 的功能
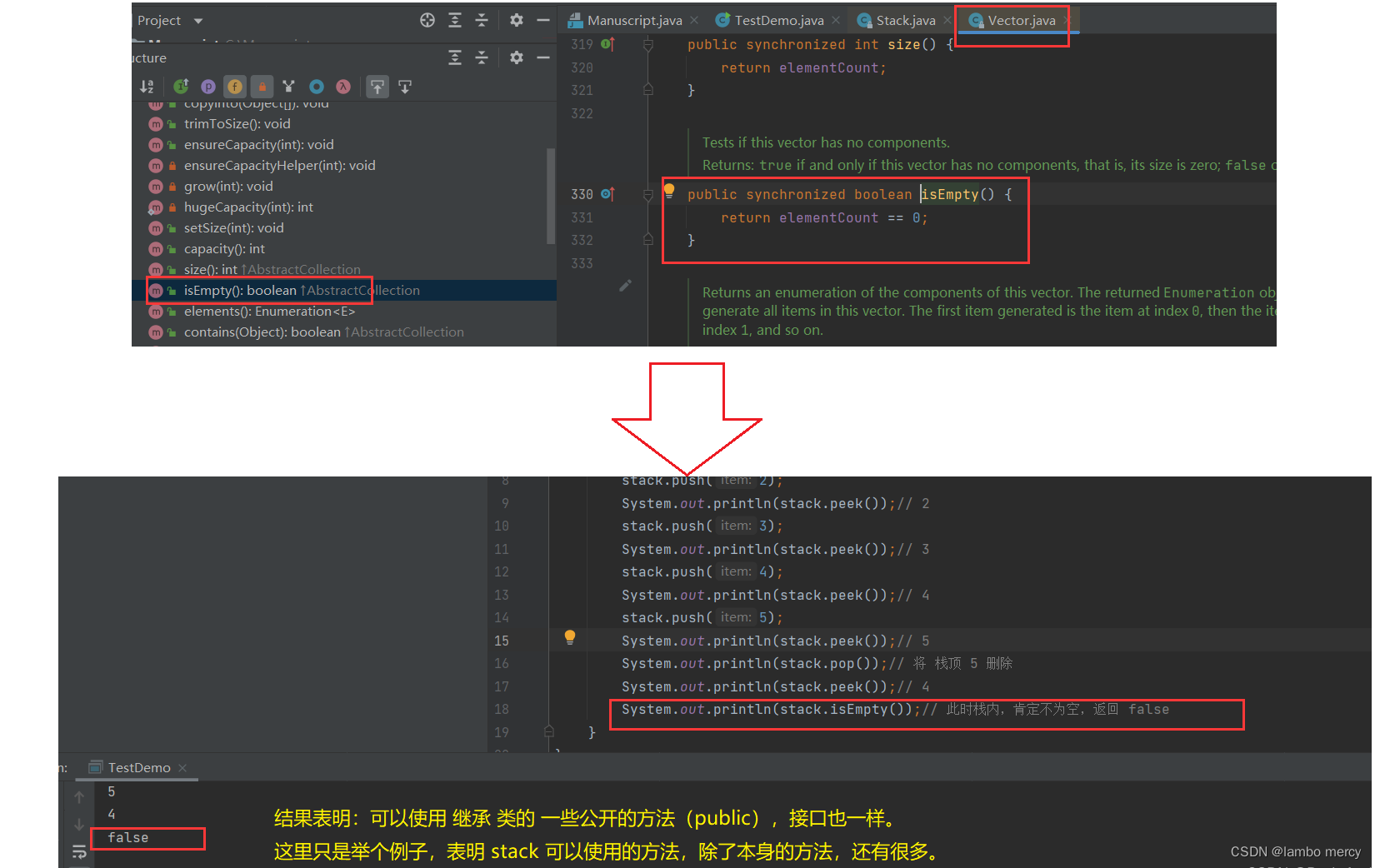
3、另外,栈继承了 Vector 类,Vectoc 类,又实现了一些接口功能。那么,就意味着:Stack 可以调用的方法不止本身的那些功能,还可以调用 它 所继承的类 和 接口 的 一些方法 和 属性。

Ctrl + 左键 进入 Vector
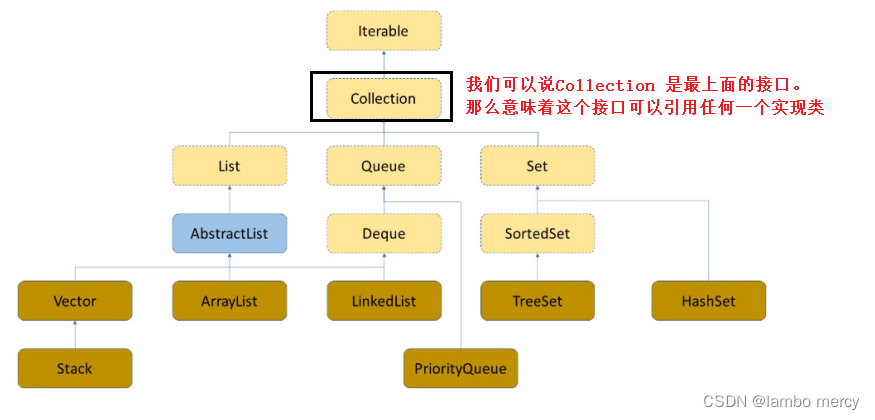
简略图
代码
class Solution {public int evalRPN(String[] tokens) {Stack<Integer> stack = new Stack<>();for(int i = 0; i <tokens.length;i++){String str = tokens[i];//获取下标为 i 字符串元素if(isOperator(str)){// 如果 str 是运算符 为 true,否则为falseint num2 = stack.pop();// 获取 栈顶 的 两个数字数据(出栈)int num1 = stack.pop();switch(str){// 判断 str 具体是 哪一个字符串,就执行对应的运算,并将其结果入栈case "+":stack.push(num1 + num2);break;case "-":stack.push(num1 - num2);break;case "*":stack.push(num1 * num2);break;case "/":stack.push(num1 / num2);break;}}else{// 将 数字字符转换成 整形数据 存入 栈中stack.push(Integer.parseInt(str));}}return stack.pop();// 返回/出栈 最终存入栈中的结果}public boolean isOperator(String s){// 判断 str 是运算符 返回 true;否则,返回 falseif(s.equals("+") || s.equals("-")|| s.equals("*") || s.equals("/")){return true;}return false;}
}
实战题
栈的压入、弹出序列_牛客题霸_牛客网 (nowcoder.com)
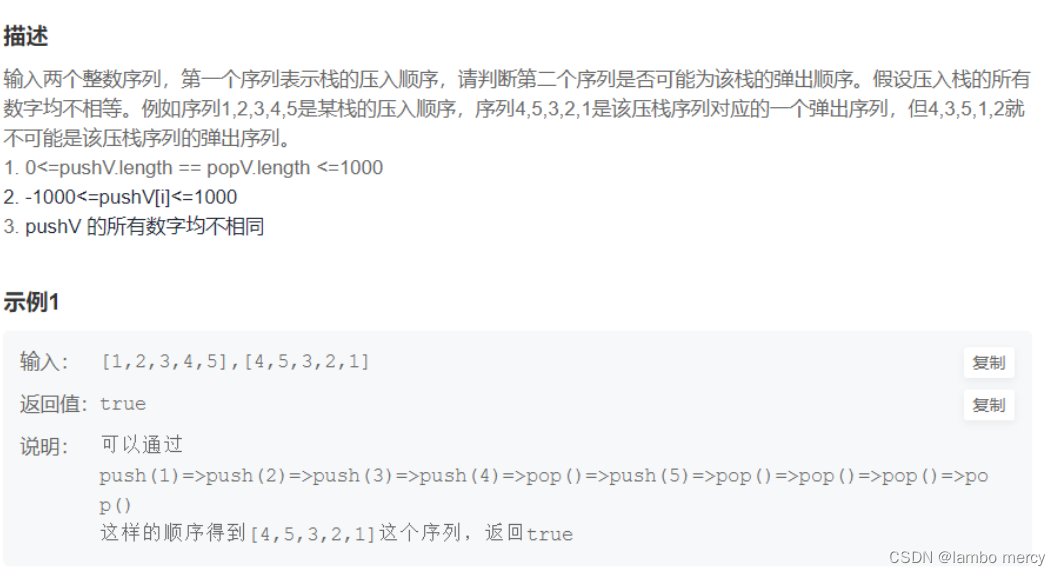
解题思维 - 双指针遍历
定义两个整形指针 p1 和 p2【初始值为0】,分别指向 输入的两个数组 pushA 和 popA
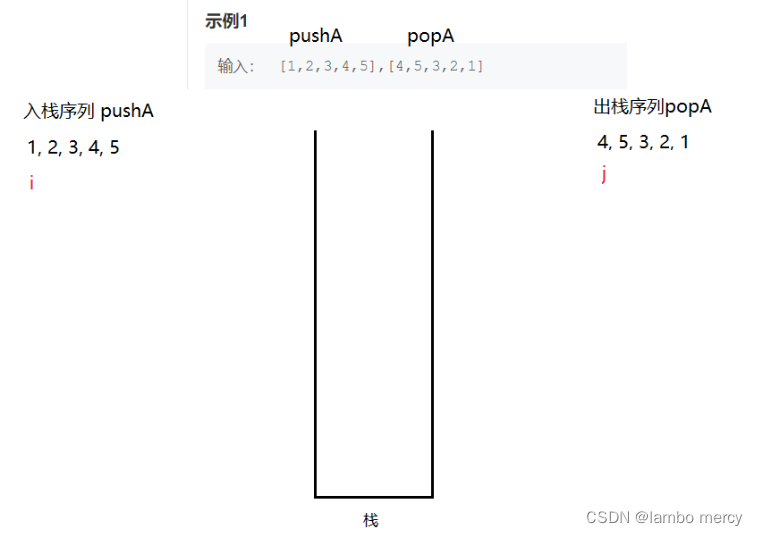
我们想法:
将 i 指向的元素入栈、入栈后,i++。直到 栈顶的数据 与 出栈序列 j 的指向相等,我们将其出栈。
然后, j++,开始判断下一个。
如果 栈顶的数据 与 出栈序列 j 指向的元素不相等。则继续 将 i 指向的数据入栈。直到 栈顶的数据 与 出栈序列 j 的指向相等,我们将其出栈。
重复此操作,直到 i 遍历完 pushA数组。
如果: 入栈数组 出栈效果 可以达到 出栈数组的效果,栈里面应该是为 空的。
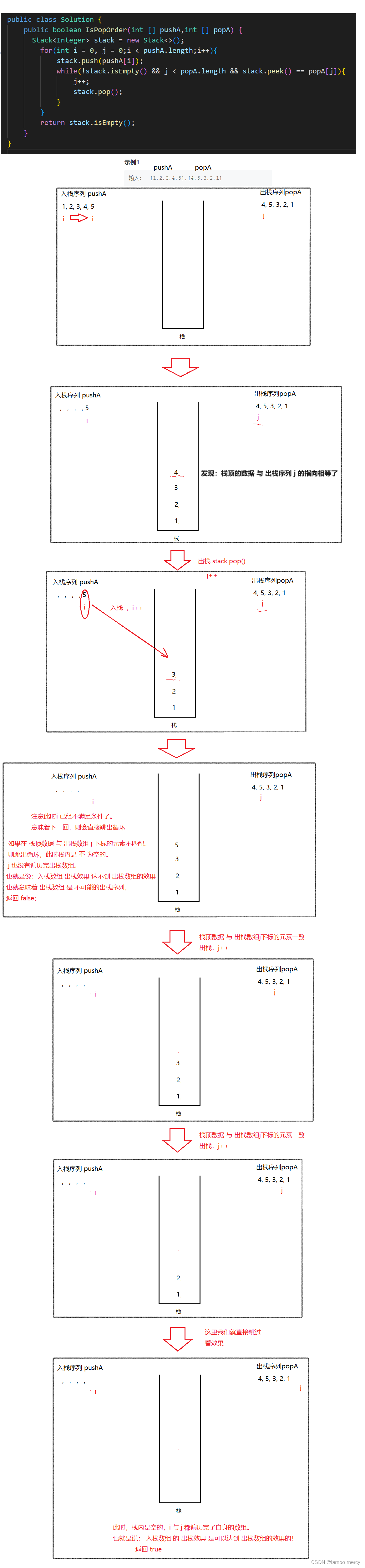
import java.util.*;public class Solution {public boolean IsPopOrder(int [] pushA,int [] popA) {Stack<Integer> stack = new Stack<>();for(int i = 0, j = 0;i < pushA.length;i++){stack.push(pushA[i]);while(!stack.isEmpty() && j < popA.length && stack.peek() == popA[j]){j++;stack.pop();}}return stack.isEmpty();}
}
模拟实现栈 - 数组实现
参考栈的源码,观察它所具有的方法 和 属性。
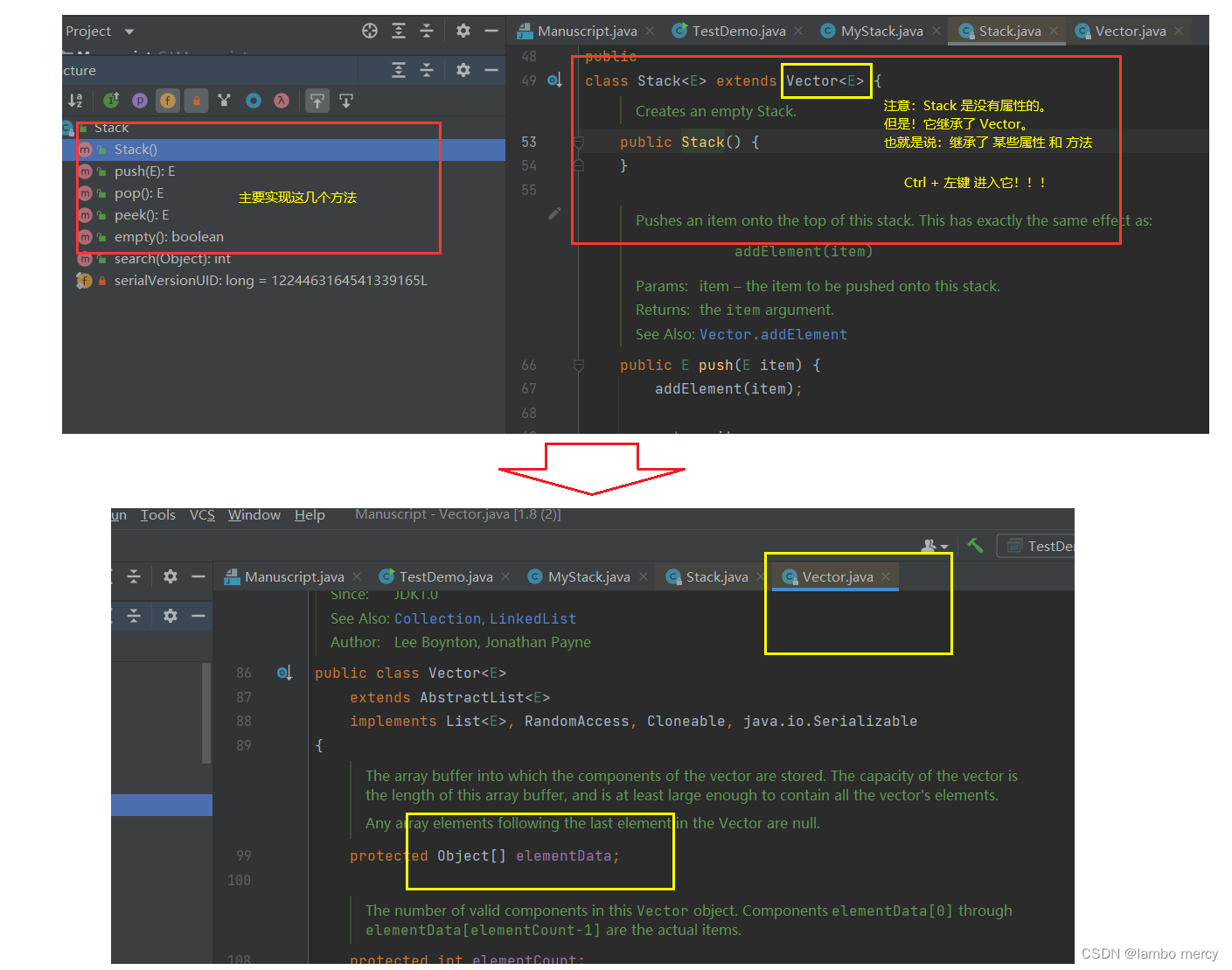
由此,得出结论:Stack 底层 也可以说是一个数组。
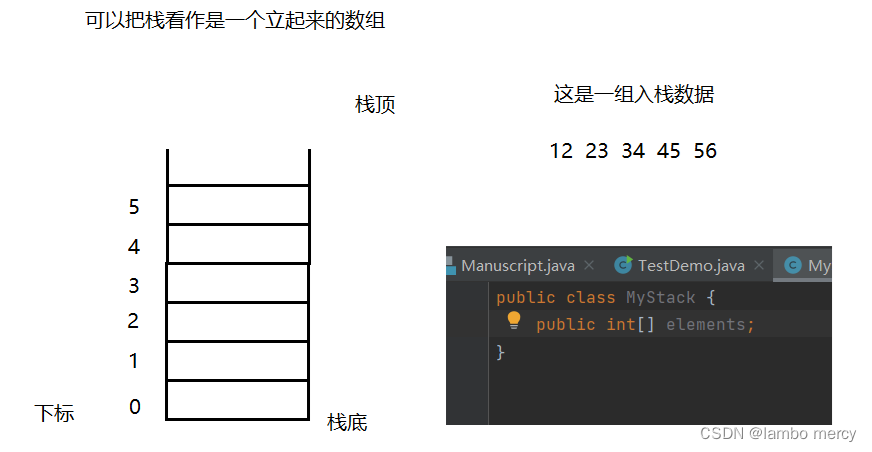
然后,就是数组的入栈了。
但是!我们需要注意:
数组的容量假设为5。但是,我该怎么知道 栈内 存储数据个数。
那么,我们就肯定需要一个 usedSize【初始值为0】 来记录 存入的数据个数。存入一个(usedSize++).
而且! 我们还可以通过它 来进行 入栈。
这么来想:当还没有存入 数据时,usedSize 为 0。此时,我们要入栈一个数据,我们 直接 elements[usedSize] = data。 然后,usedSize++:【细品一下:在将原先的数据“入栈”到对应的位置后,usedSize再++。是不是记录了入栈的元素个数,又为下一次入栈的数据,指定好了位置】
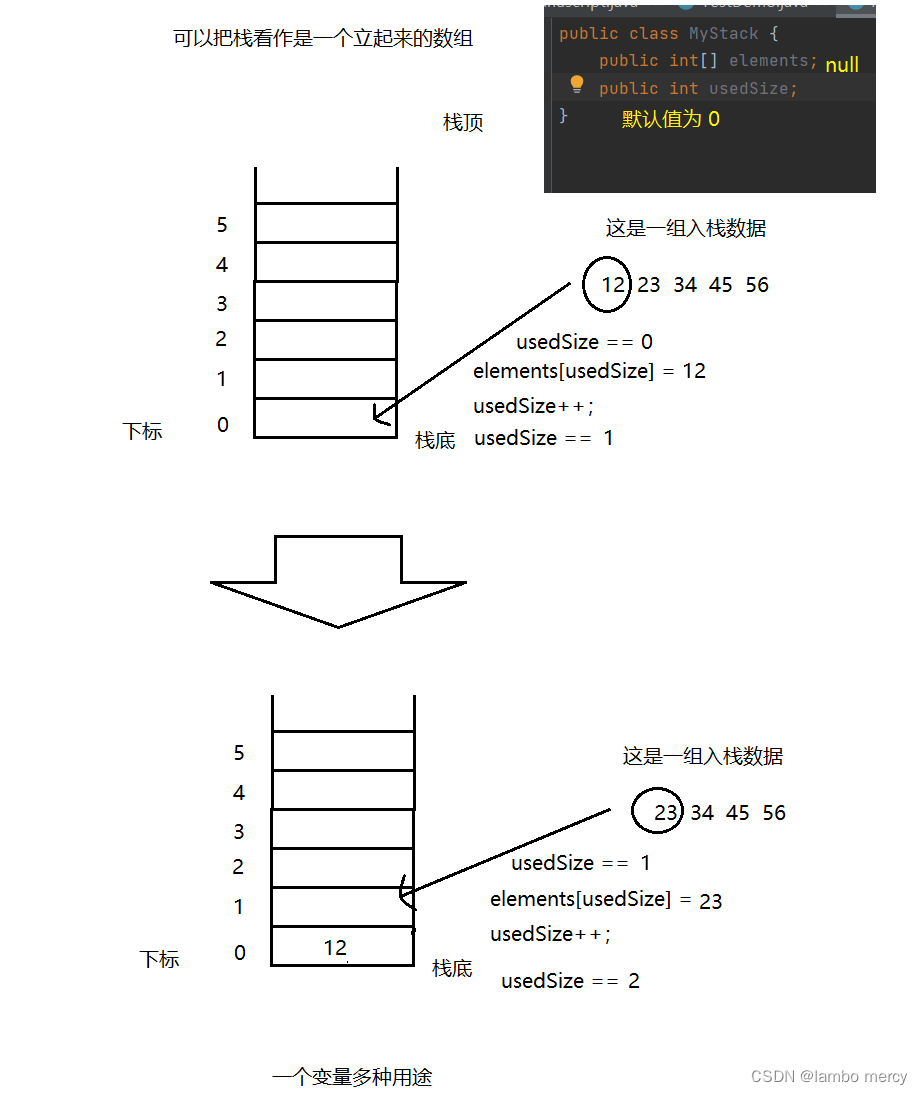
之后,就是构造一个 Stack 的 构造方法。【将底层数组初始容量定为5】
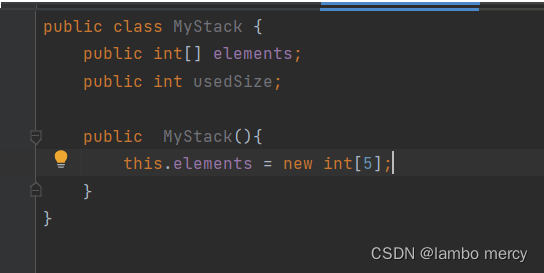
实现栈的功能
1、 push 入栈 功能
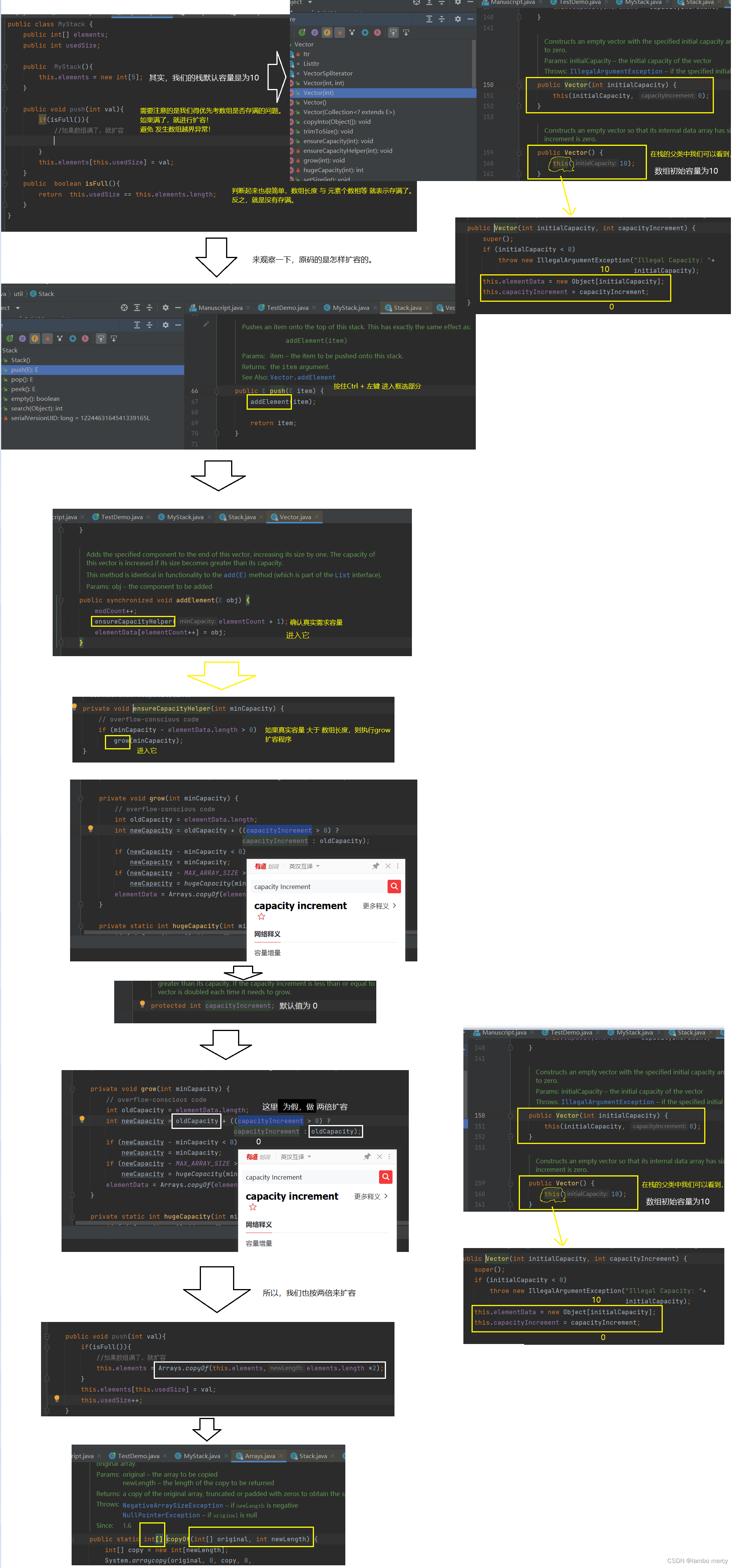
pop 出栈功能
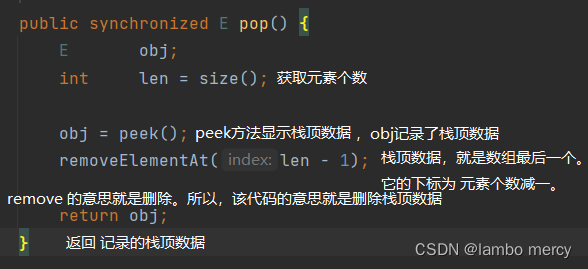
注意!此时,我们的栈是利用数组来实现了。

peek 方法
peek 方法只是获取栈顶元素,并不涉及删除。所以,usedSize 就不用再减减了
模拟 Stack(栈) 总程序附图
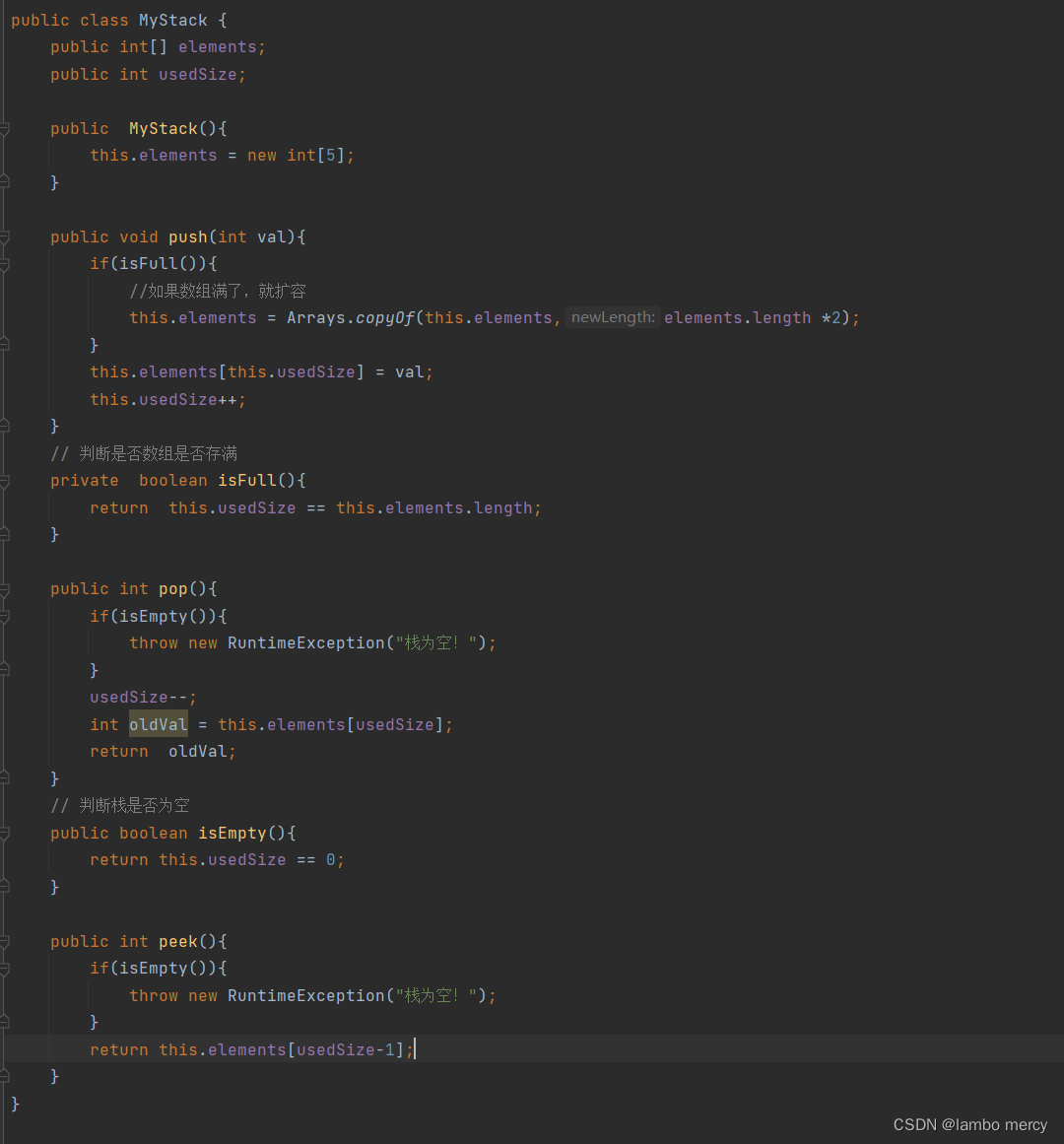
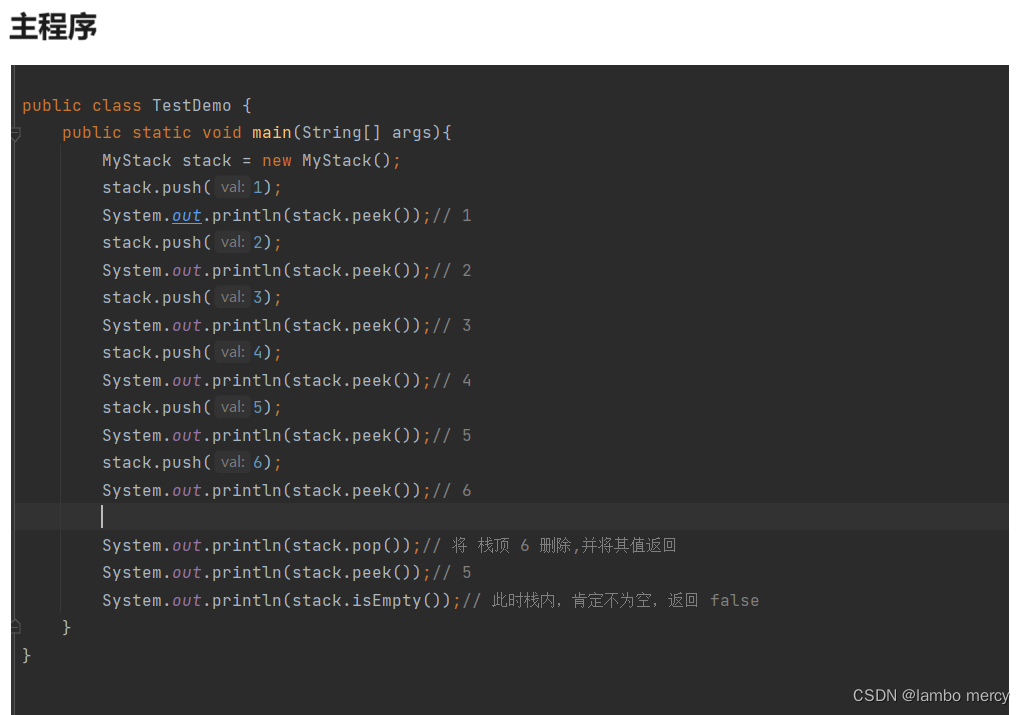
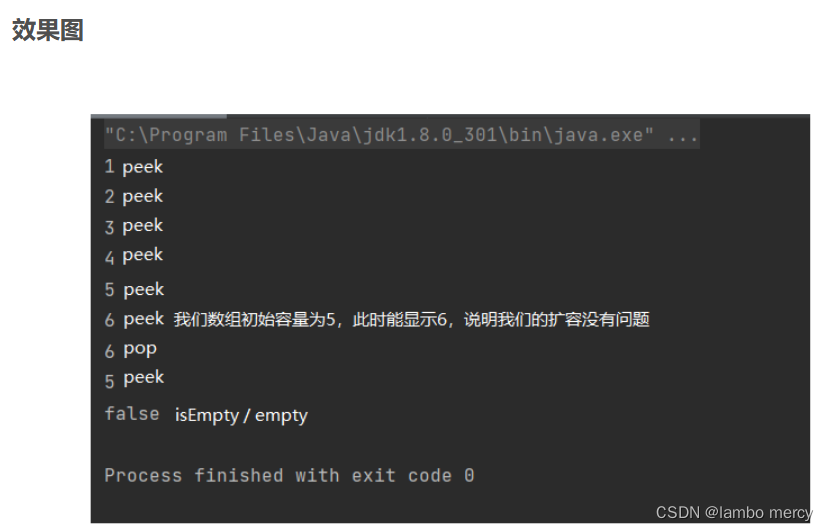
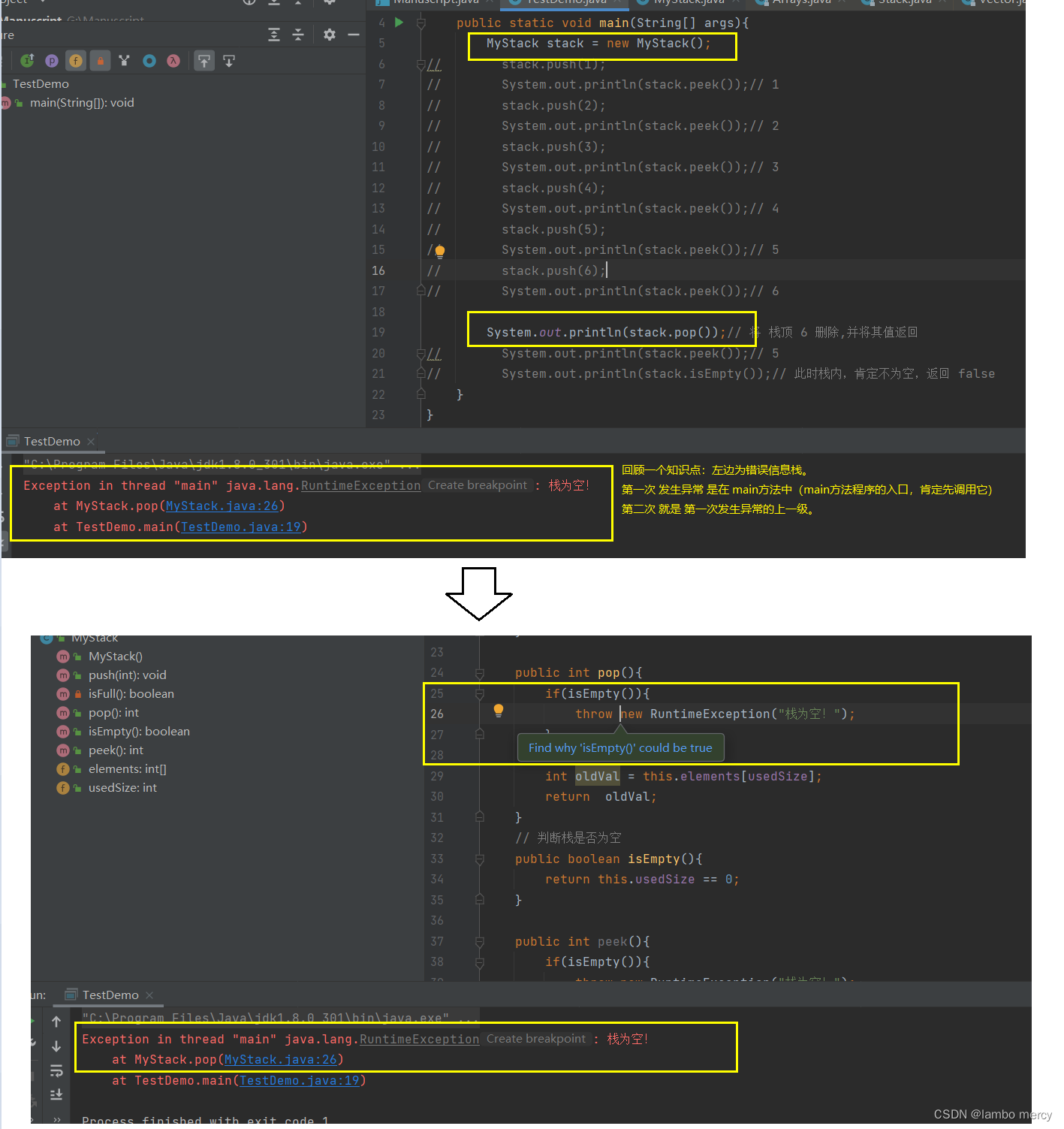
模拟实现栈 - 链表实现
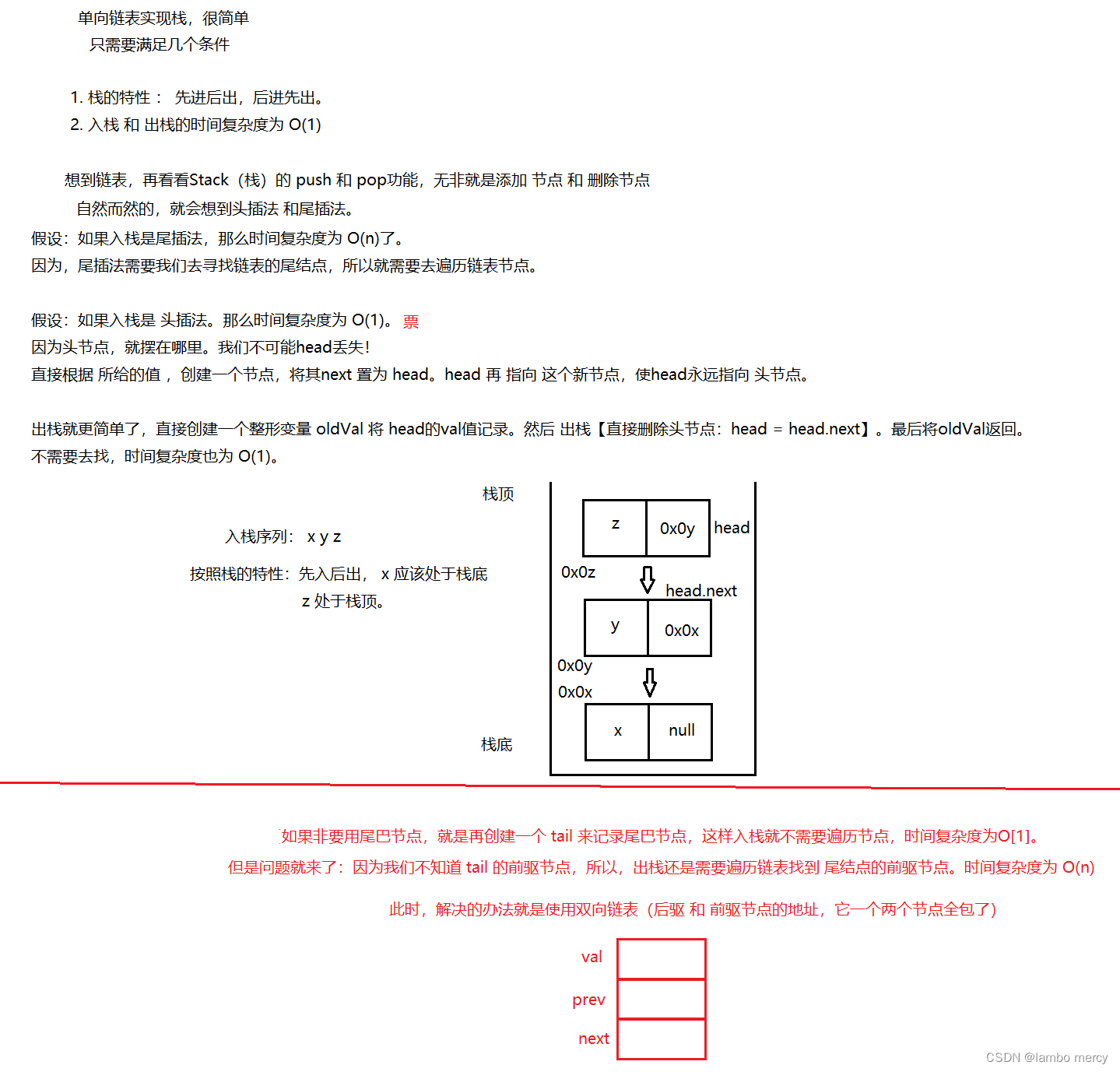
单向链表 + 头插
class Node{int val;Node next;public Node(){}public Node(int val,Node node){this.val = val;this.next = node;}}public class MyStackLinked {Node head;// 头节点 : 标记栈顶public void push(int x){Node node = new Node(x,head);this.head = node;}public int pop(){if(isEmpty()){throw new RuntimeException("栈为空");}int oldVal = this.head.val;head = head.next;return oldVal;}public boolean isEmpty(){return this.head == null;}public int peek(){if(isEmpty()){throw new RuntimeException("栈为空");}return head.val;}
}双向链表 + 尾插
class DoubleNode{int val;
// DoubleNode next;// next 用不到,加不加都不影响效果DoubleNode prev;public DoubleNode(int val,DoubleNode prev){this.val =val;this.prev = prev;}
}public class MyStackDoubleLinked {
// DoubleNode head; 头节点 用不到DoubleNode tail;public void push(int x){if(tail == null){tail = new DoubleNode(x,tail);}else{DoubleNode node = new DoubleNode(x,tail);
// tail.next = node; 如果你还是加 next,这一步我给你准备好了tail = node;}}public int pop(){if(isEmpty()){throw new RuntimeException(" 栈为空 ");}int oldVal = tail.val;tail = tail.prev;return oldVal;}public boolean isEmpty(){return tail == null;}public int peek(){if(isEmpty()){throw new RuntimeException(" 栈为空 ");}return tail.val;}
}
栈的面试题
LeetCode - 20. 有效的括号
解题思维
这道题跟前面 逆序波兰表达式,做法思维是相同的。
遍历 字符串,当我们 遇到 ’ ( ’ 、’ [ ‘、’ { ’ 的 时候,我们就将它入栈。
随后,继续便来字符串。直到遇到 ’ ) ‘、’ ] ‘、’ } '。我们就去判断栈顶的数据 是不是 它们对应的做符号。如果是:出栈(将栈顶数据出栈,表示这对括号有效)。反之,如果不是:直接返回 false。【因为这个乱入的符号导致整个字符串的符号无法匹配】。再或者:遍历完了字符串,栈里面还存储的左符号,没有右符号匹配了,直接返回false;
之所以说与逆波兰表达式那题相同,就是遇到了特定字符需要进行相应的操作,返回值还是需要根据 栈的内部情况决定【空为ture,否则为 false(为 true,说明字符串里面的括号都是有效的)】
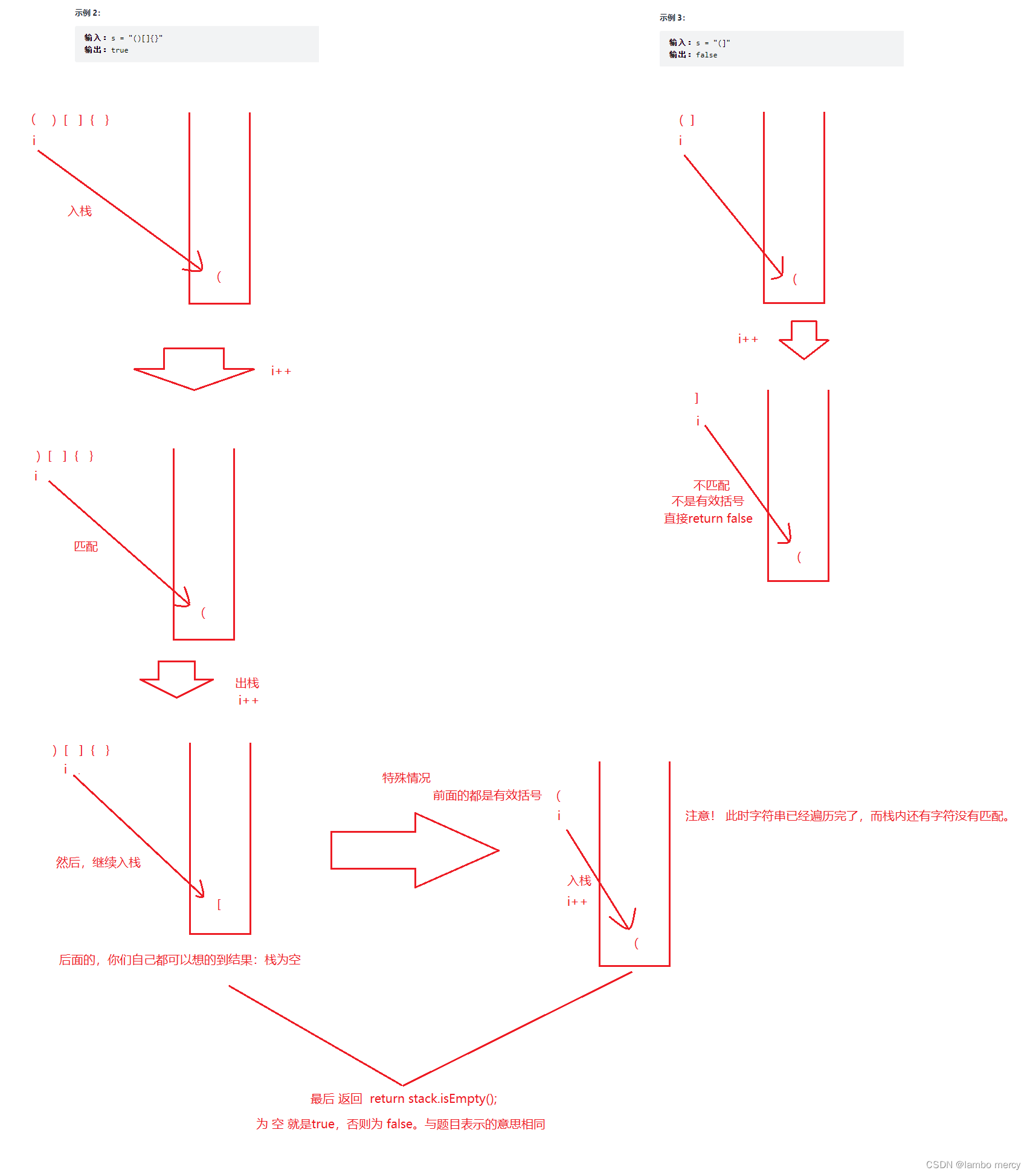
代码如下
class Solution {public boolean isValid(String s) {Stack<Character> stack = new Stack<>();for(int i = 0;i < s.length();i++){char ch = s.charAt(i);if(ch == '(' || ch == '[' || ch == '{'){stack.push(ch);}else{if(stack.isEmpty()){return false;}char top = stack.peek();if(top == '(' && ch == ')'){stack.pop();}else if(top == '[' && ch == ']'){stack.pop();}else if(top == '{' && ch == '}'){stack.pop();}else{return false;}}}return stack.isEmpty();}
}
155. 最小栈
这题大概是这么个意思:要求我们实现一个栈,能以时间复杂度O(1),找到栈中最小的元素。
其中 top ,其实就是 peek方法:查看栈顶数据。
解题思维
首先,我们需要明白一个问题:能以时间复杂度O(1),找到栈中最小的元素是不可能的。
因为需要再遍历数组一遍,才能确定最小值。时间复杂度达到O(N)…
那么,既然一个不行,那我两个!
来看我怎么做:
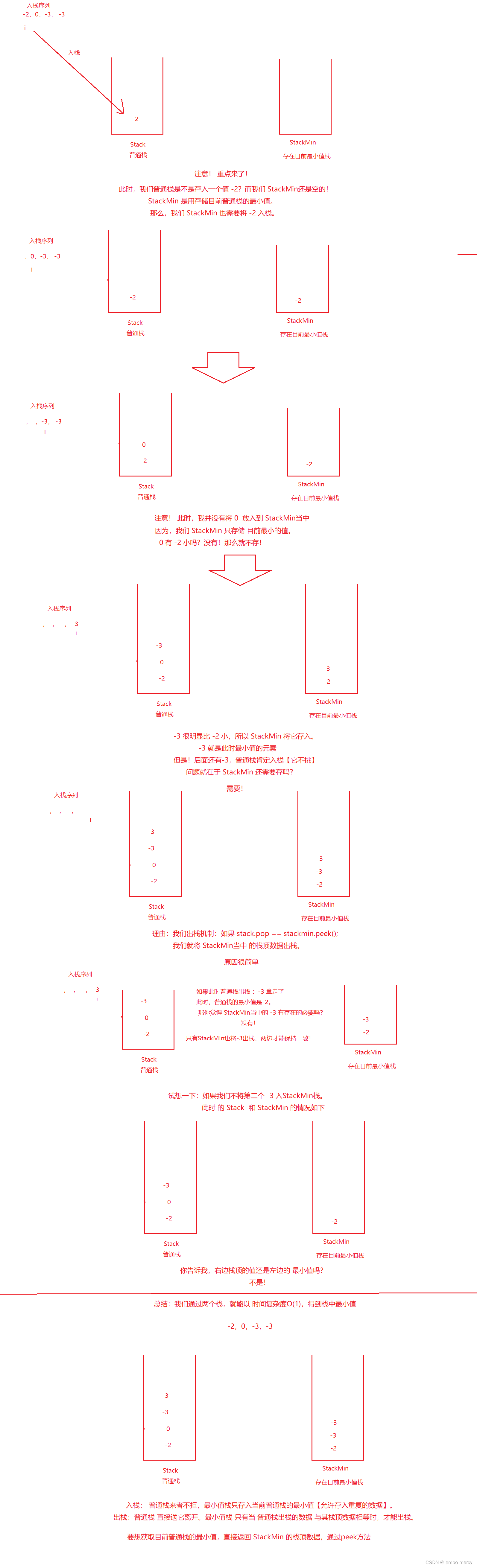
代码如下
class MinStack {private Stack<Integer> stack;private Stack<Integer> stackMin;public MinStack() {stack = new Stack<>();stackMin = new Stack<>();}//入栈public void push(int val) {stack.push(val);if(stackMin.isEmpty()){stackMin.push(val);}else{if(val <= stackMin.peek()){stackMin.push(val);}}}// 出栈public void pop() {if(!stack.isEmpty()){int val = stack.pop();if(val == stackMin.peek()){stackMin.pop();}}}// 等价于 peek方法public int top() {return stack.peek();}// 和获取 目前 Stack 栈中最小值public int getMin() {return stackMin.peek();}
}
队列
普通队列【queue】:只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出FIFO(First In First Out) 入队列:进行插入操作的一端称为队尾(Tail/Rear) 出队列:进行删除操作的一端称为队头。
双端队列【deque】: 出队 和 入队,则没有像普通队列那样的限制。 无论是 队头 还是 队尾,都可以出入队。
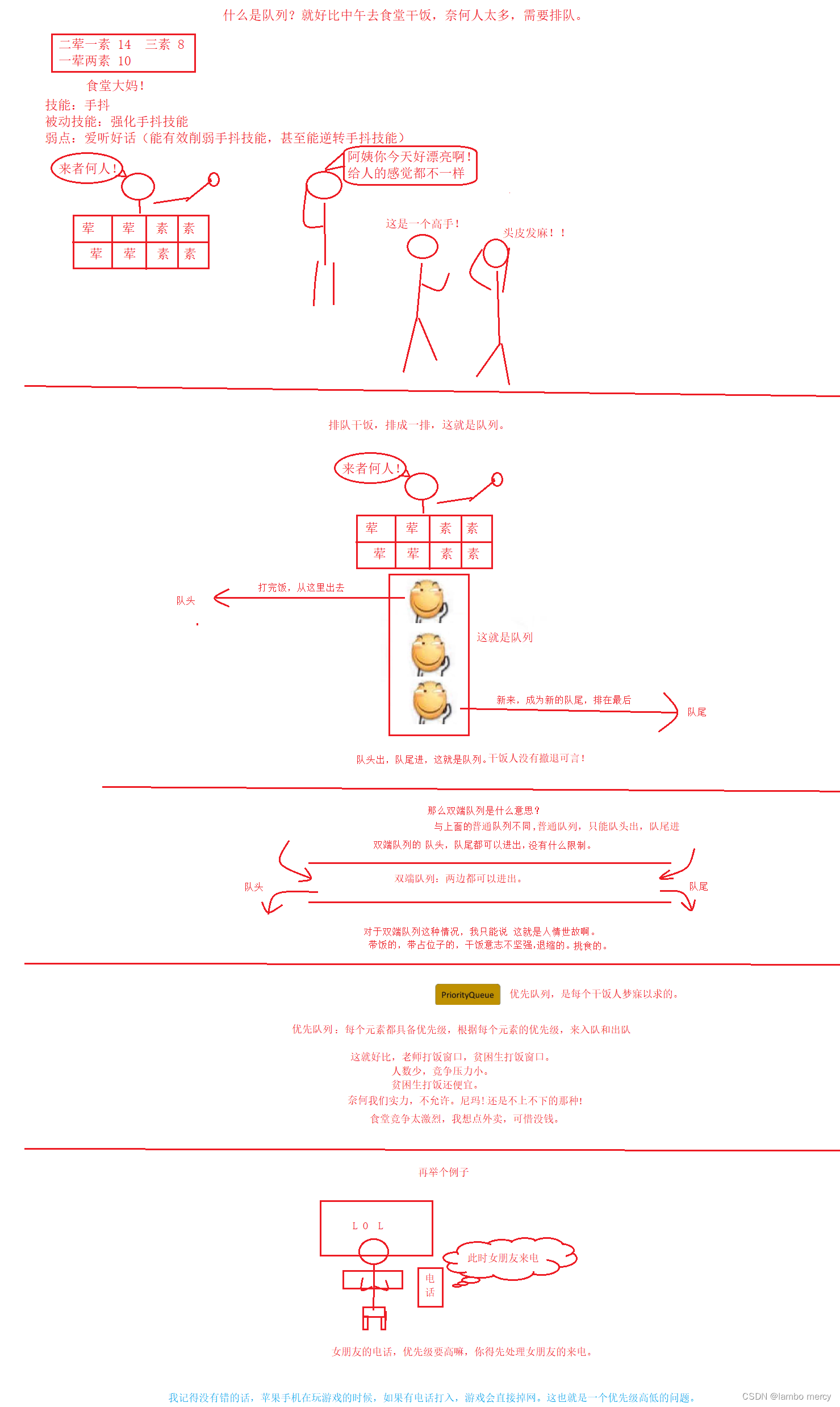
看过上面的图,我们 可以知道 双向队列,可以用来实现 栈 。因为队尾队头都可以入出对,也就是说肯定会有一个 标识 队头 和 队尾的属性,我们就可以通过这个来用队列 实现 栈 。(这个deque 会有相对应的功能 可以用来实现 栈,可以参考下方的 deque 功能展示)
再来看看 集合框架背后的数据结构图。
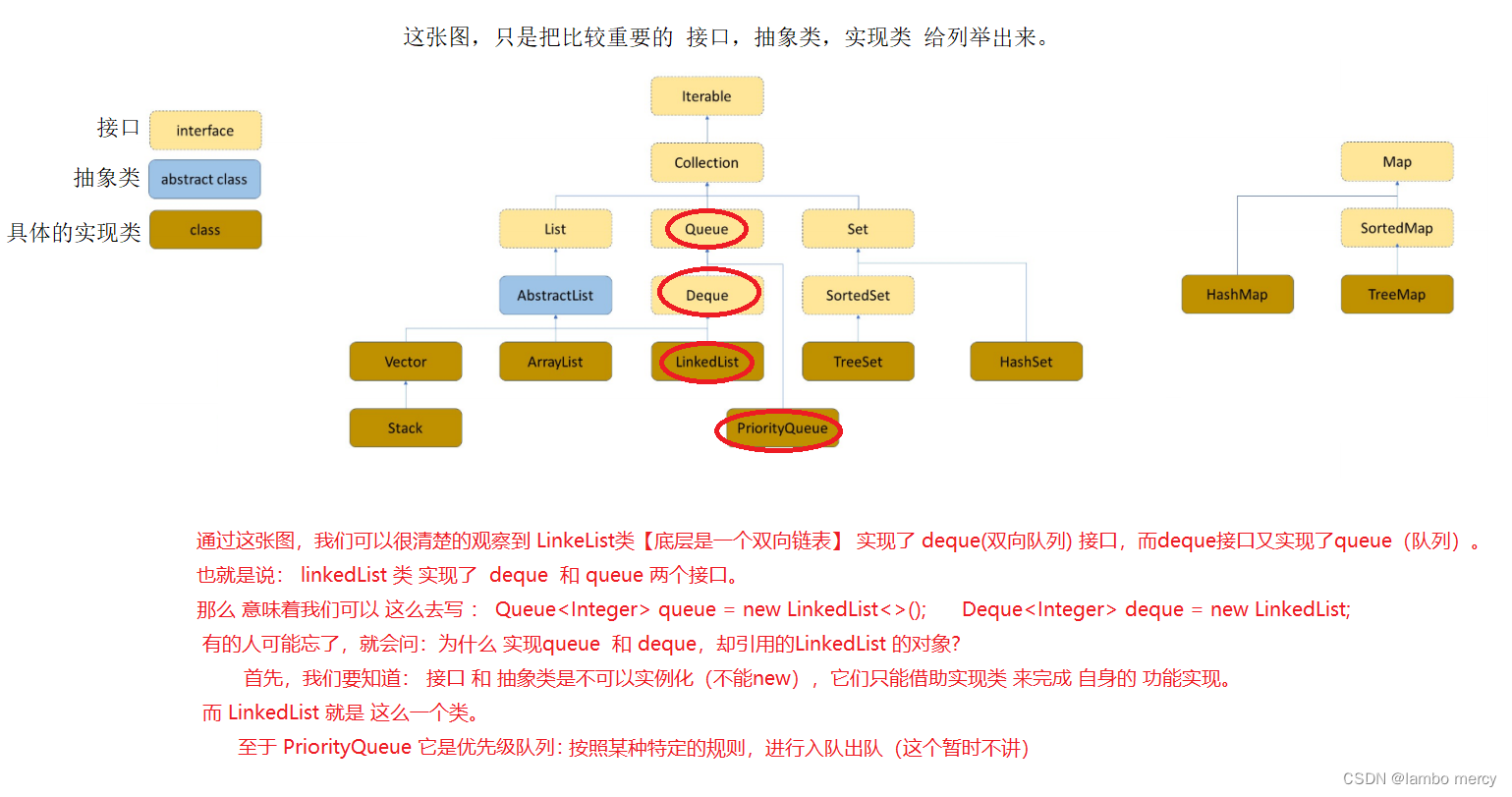
当然也可以 直接通过 LinkedList 实现类 来 new LinkedList 对象。因为 LInkedList 类 实现了 deque 和 queue。再加上它自身的功能,说明LinkedList 的功能 只会 更多。
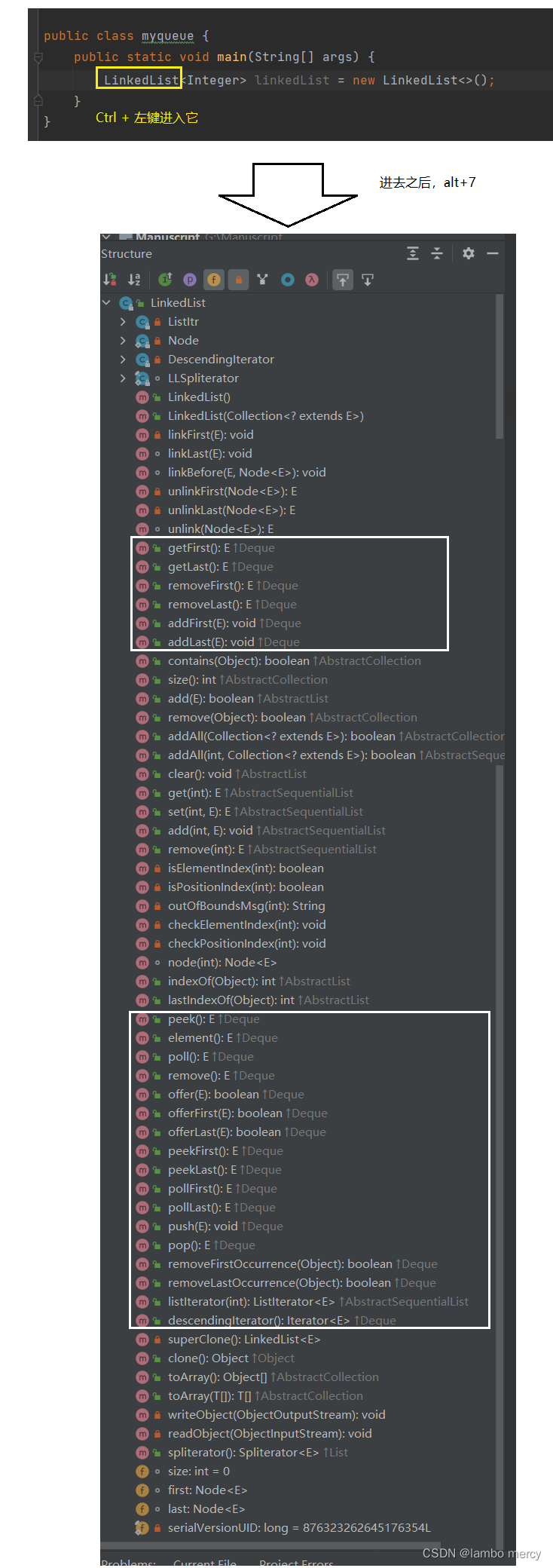
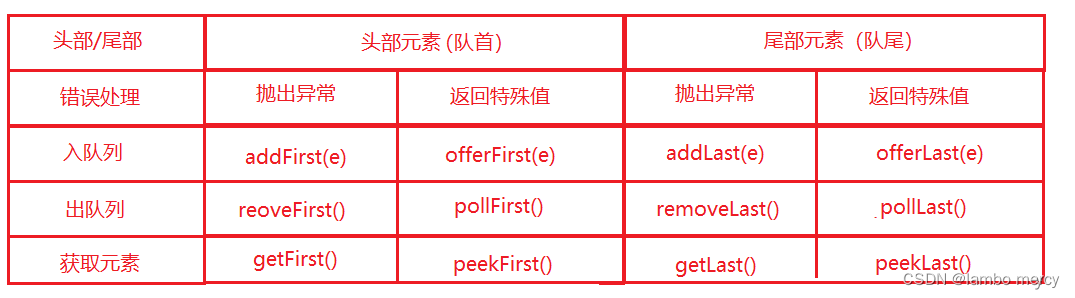
queue【队列】 和 deque【双端队列】所具有的功能

普通队列 queue 基础功能 分析 与 区别
add 和 offer 入栈方法的区别
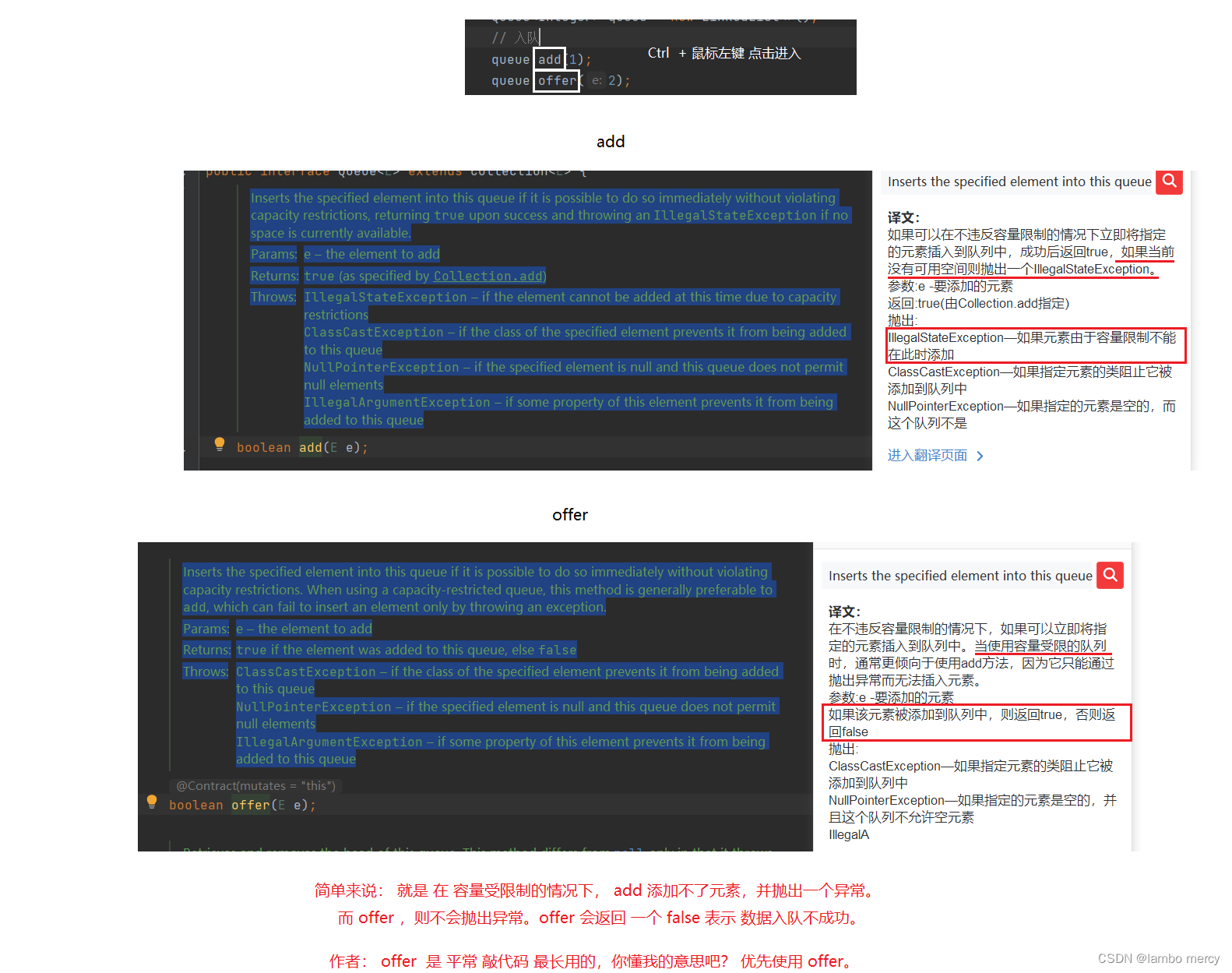
peek 和 element 返回队顶数据 方法的区别
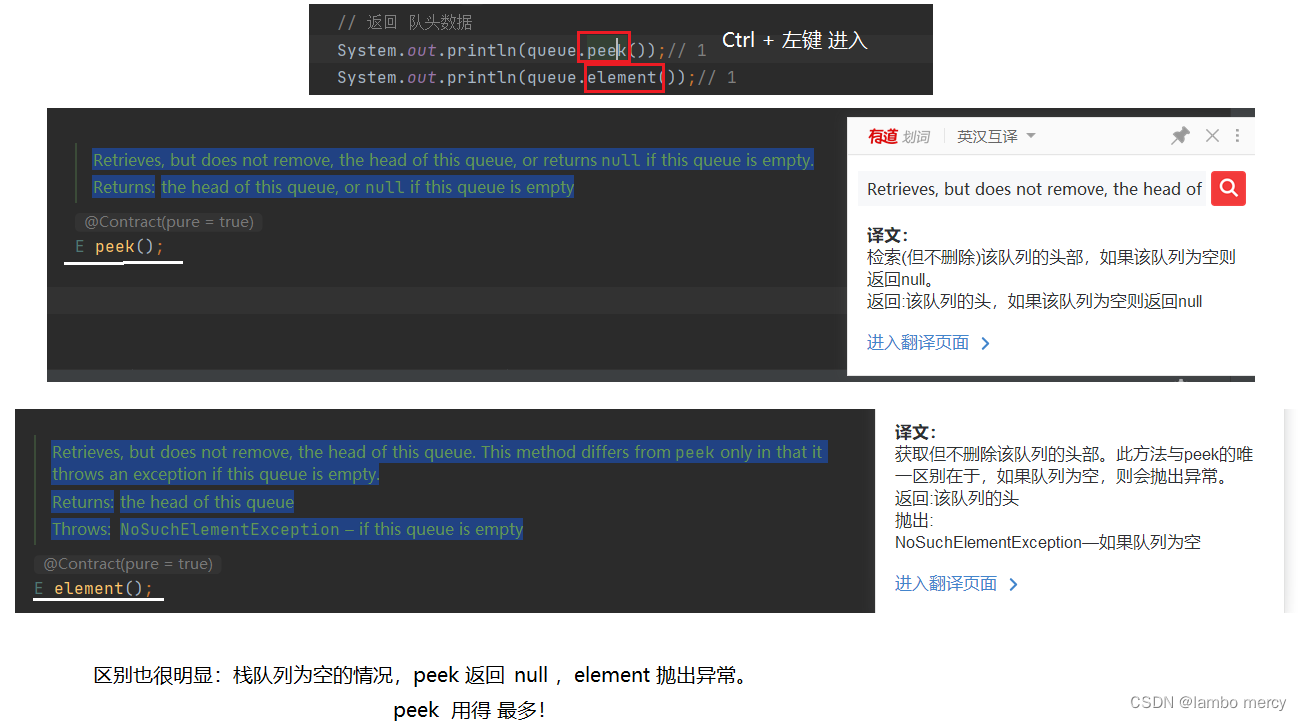
poll 和 remove 出队方法的区别
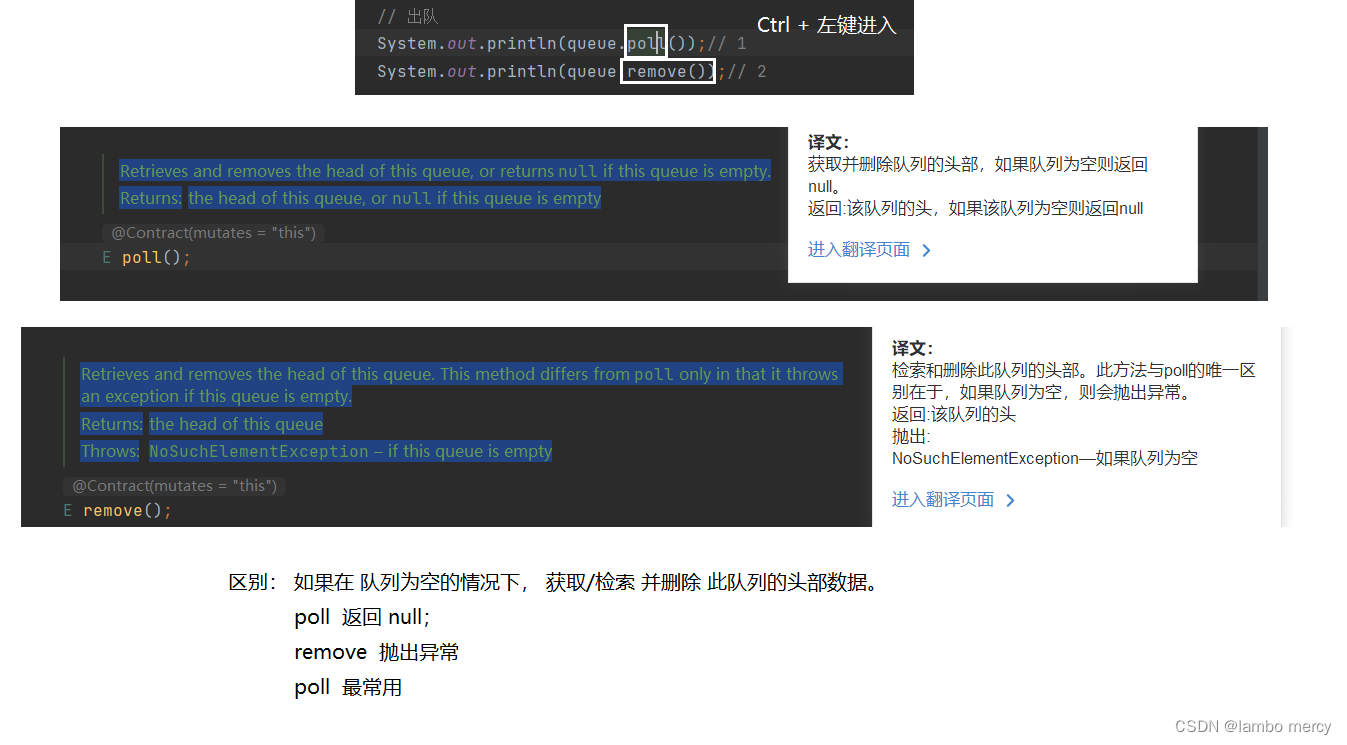
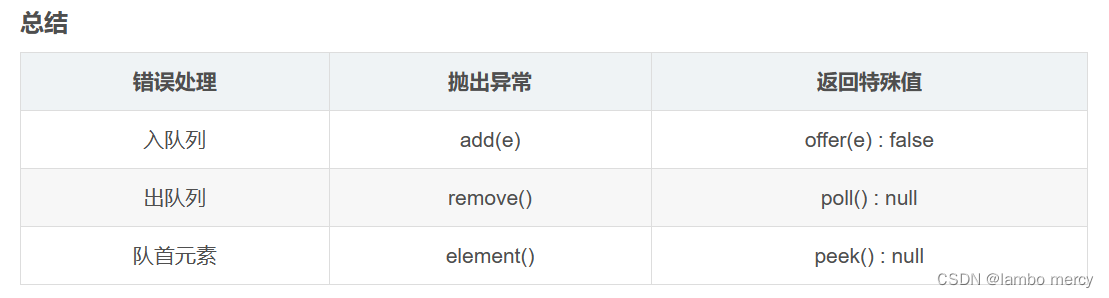
双端队列【deque】的基础功能演示
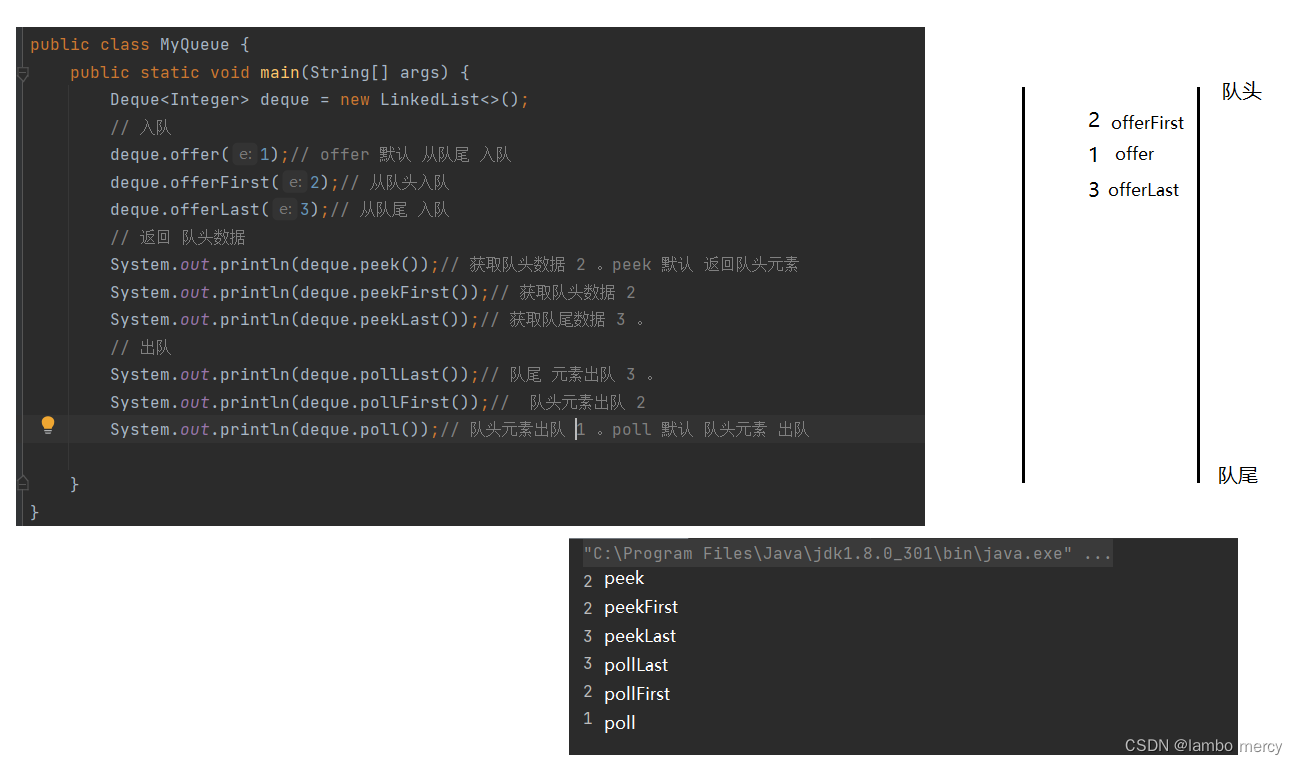
功能细节
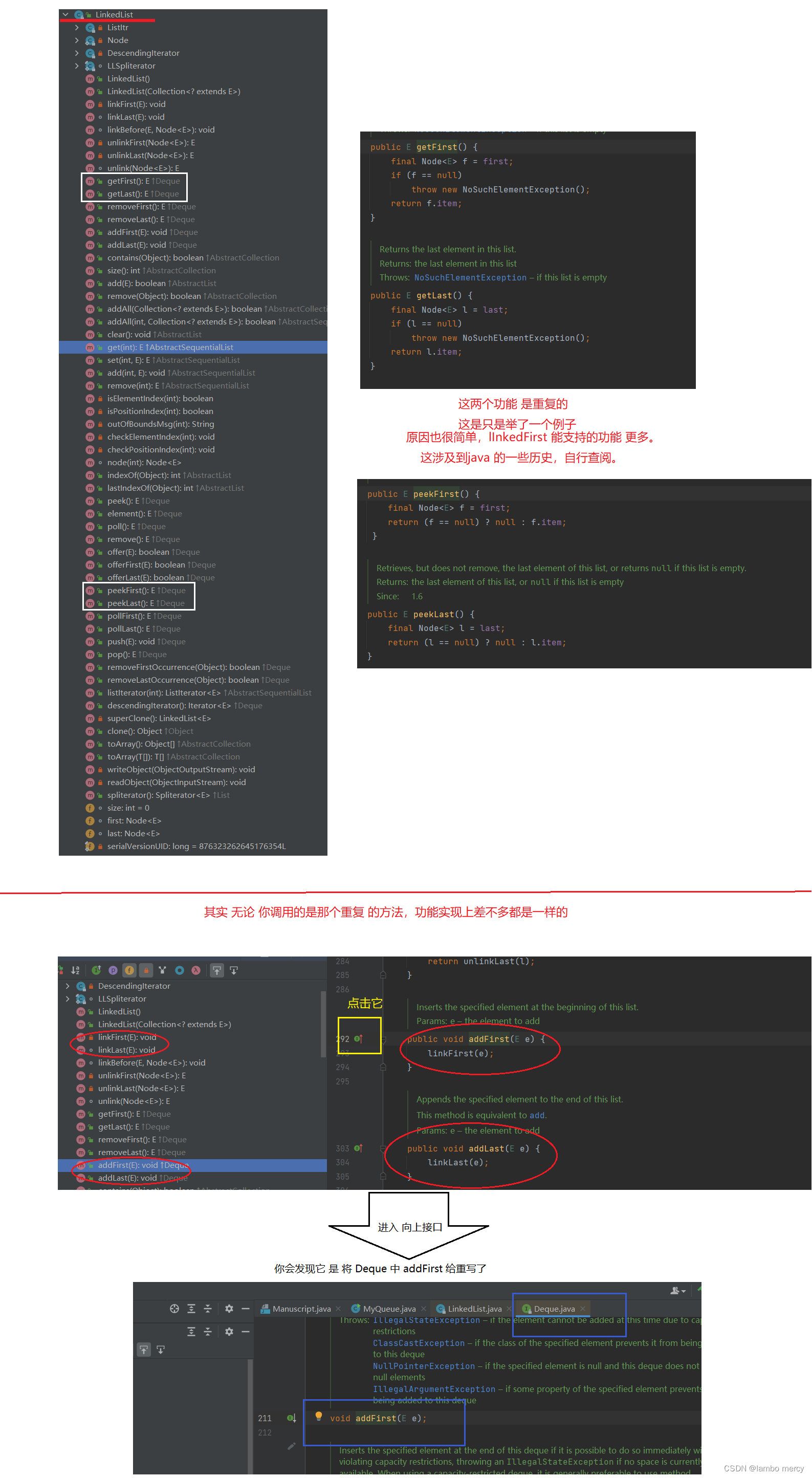
讲这个是为了表明一个点:如果只是一些简单的方法,可以通过接口去引用。不用直接去new 实现类
总结
特殊值返回值 和 异常,跟上的普通队列返回值是一样的。
返回特殊值的方法,都是最常用的方法。
总结
对于 LinkedList 来说:它不仅可以当作普通的队列、双端队列、双向链表,栈 来使用。
对于 LinkedList 来说,它有一项比较尴尬的功能 addIndex 给 某个下标添加一个元素
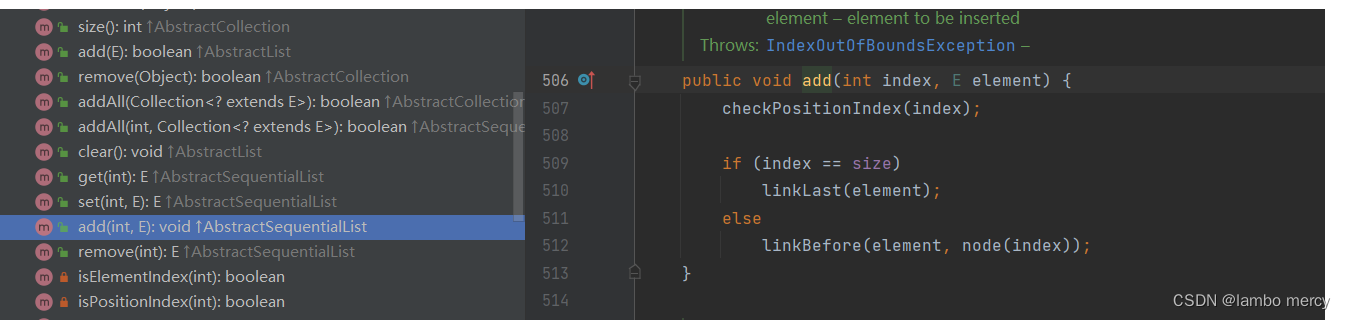
要知道,链表是没有下标的!
由此引申出 一个问题 :
顺序表 和 链表 的区别是什么?
ArrrayList 和 LinkedList 的区别是什么?(这个问的最多)
解答:
1、从共性出发:增删查改
【ArrrayList支持 随机 访问,LinkedList不支持。因为链表没有下标】
【 LinkedList 删除和添加元素 时间复杂 ArrrayList 要比 低,因为 不需要像顺序表做整体的位移。】
2、 从内存的逻辑出发
【ArrrayList 是一个顺序存储(底层为一个数组) ,内存 在 理论 和 物理上 都是 连续的】
【 LinkedList 是一个链式存储(由一个个节点连接而成),内存在理论上是连续的,在物理上不是连续的(因为不可能说每次new的节点,都是和原来的节点是紧挨着的!因为 new 对象,它是哪里有位置,它new哪里,没有规律的)】
模拟实现 普通队列(Queue) - 单链表实现。
需要考虑的一点就是 哪边当队头,哪边当队尾?
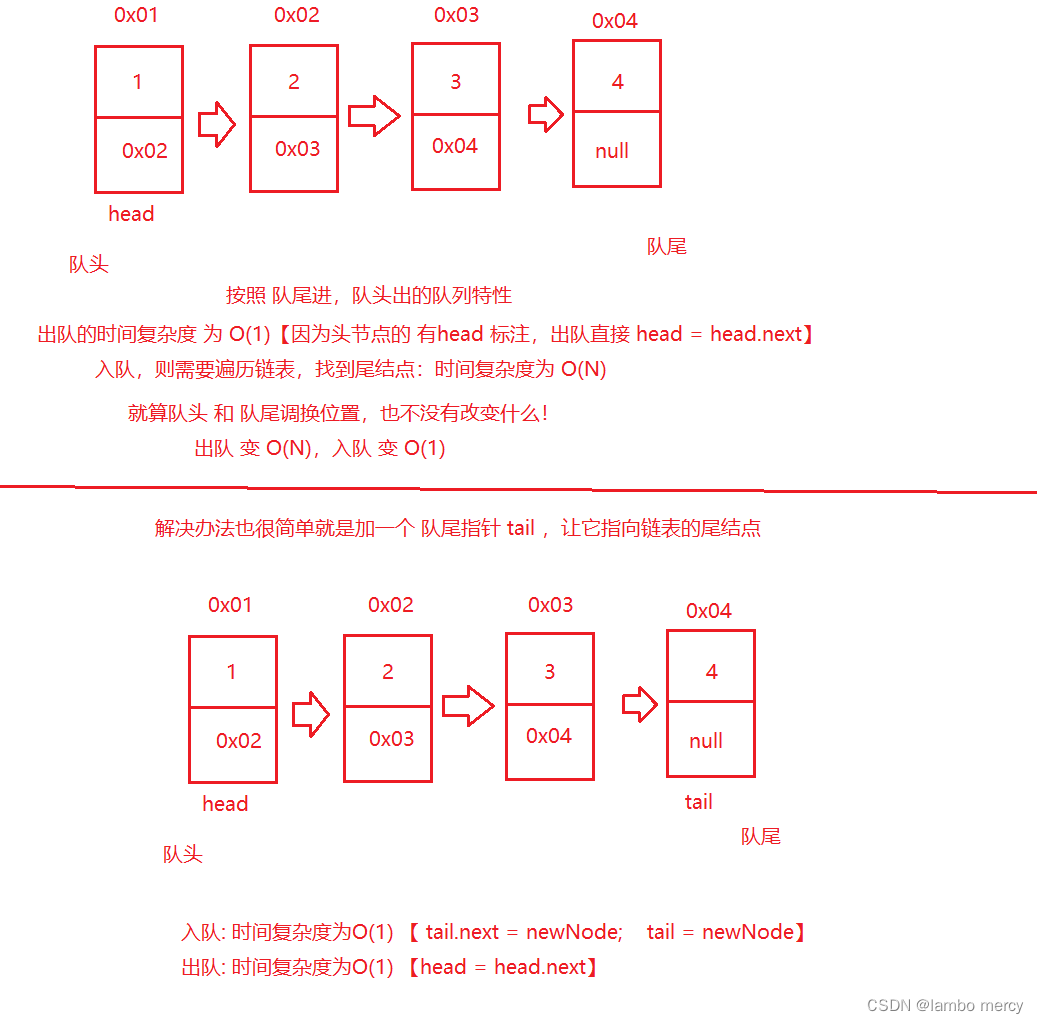
当然,你可以用双向链表来实现,那就很简单了!!! 所以我们这里才使用 单向链表实现
代码如下
public class TestDemo {public static void main(String[] args) {MyQueue myQueue = new MyQueue();myQueue.offer(1);// 入队myQueue.offer(2);// 出队try{System.out.println(myQueue.poll().val);// 1}catch (NullPointerException e){e.printStackTrace();System.out.println("队列为空 【poll】");}// 返回头数据try {System.out.println(myQueue.peek().val);// 2}catch (NullPointerException e){e.printStackTrace();System.out.println("队列为空【peek】");}}
}附图

主程序2
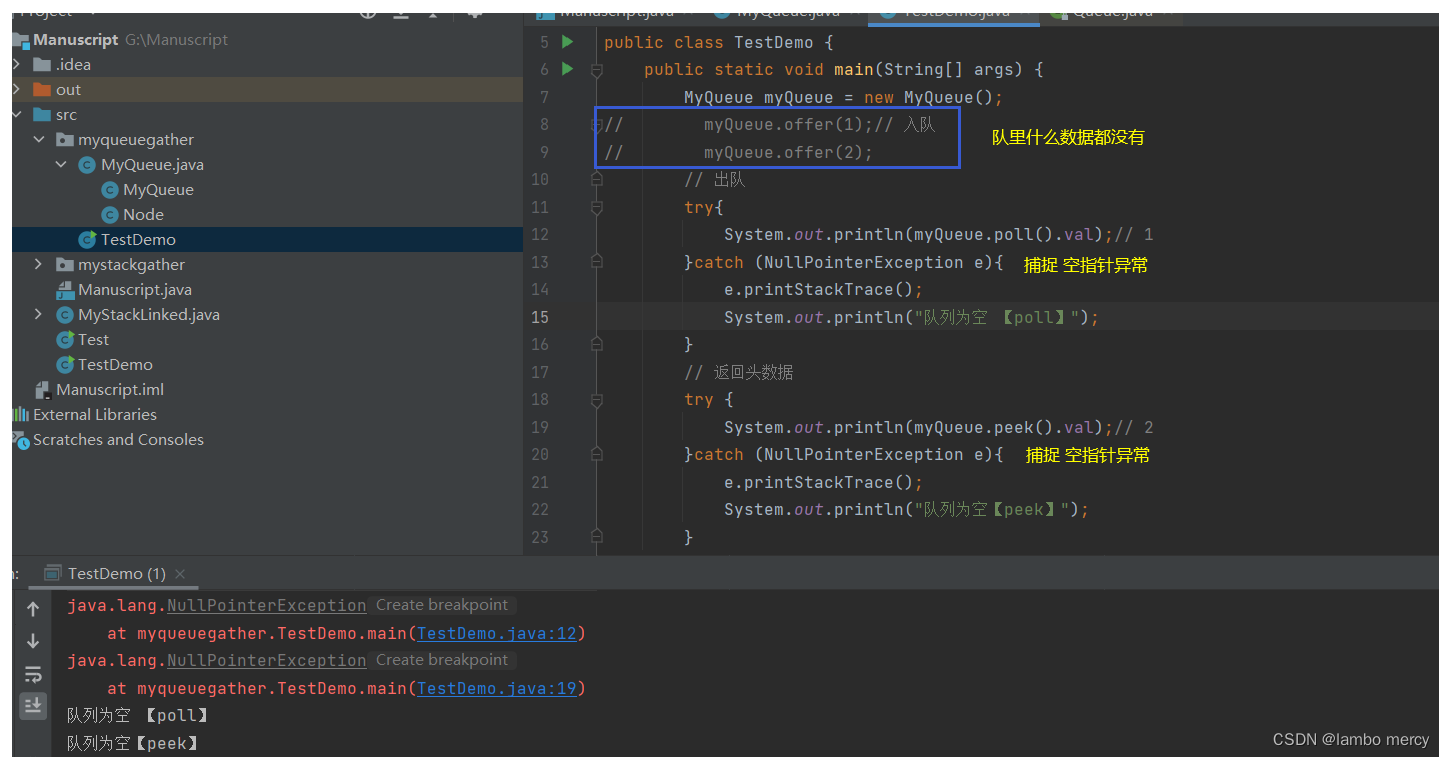
队列实现
public class MyQueue {Node head;// 队头Node tail;// 队尾public void offer(int x){if(head == null){// 第一次入队head = new Node(x);tail = head;}else{// 从队尾 入队tail.next = new Node(x);this.tail = this.tail.next;}}public Node poll(){if(head == null){// 队列为 空,返回 nullreturn head;}Node node = head;this.head = head.next;return node;// 返回删除的头}public Node peek(){return head;}}
循环队列
实际中我们有时还会使用一种队列 叫 循环队列。如操作系统课程讲解生产者消费者模型时可以就会使用循环队列。
环形队列通常使用数组实现。
队列面试题
LeetCode - 622. 设计循环队列
解题思维 与 步骤 - 使用第三种判断循环队列的方法
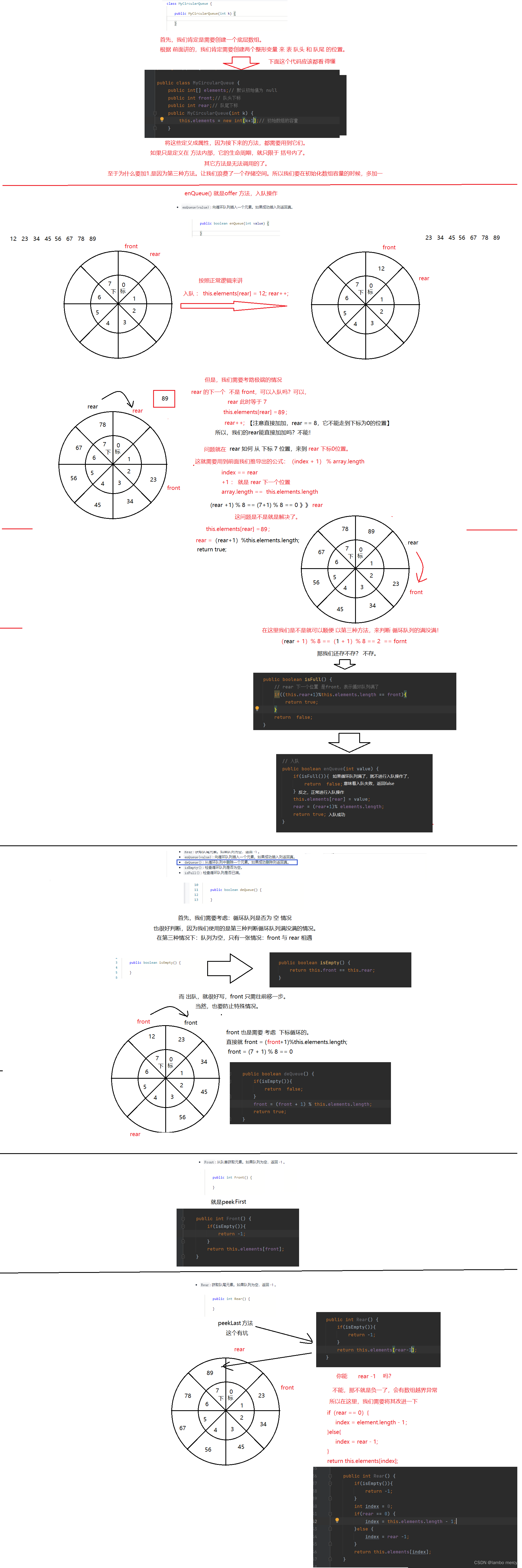
代码如下
class MyCircularQueue {int[] elements;int front;int rear;public MyCircularQueue(int k) {elements = new int[k+ 1];}public boolean enQueue(int value) {if(isFull()){return false;}elements[rear] = value;rear = (rear+1)%elements.length;return true;}public boolean deQueue() {if(isEmpty()){return false;}front = (front+1)%elements.length;return true;}public int Front() {if(isEmpty()){return -1;}return elements[front];}public int Rear() {if(isEmpty()){return -1;}int index = 0;if(rear == 0){index = elements.length - 1;}else{index = rear - 1;}return elements[index];}public boolean isEmpty() {return front == rear;}public boolean isFull() {if((rear+1)%elements.length == front){return true;}return false;}
}
LeetCode - 232. 用栈实现队列
解题思维
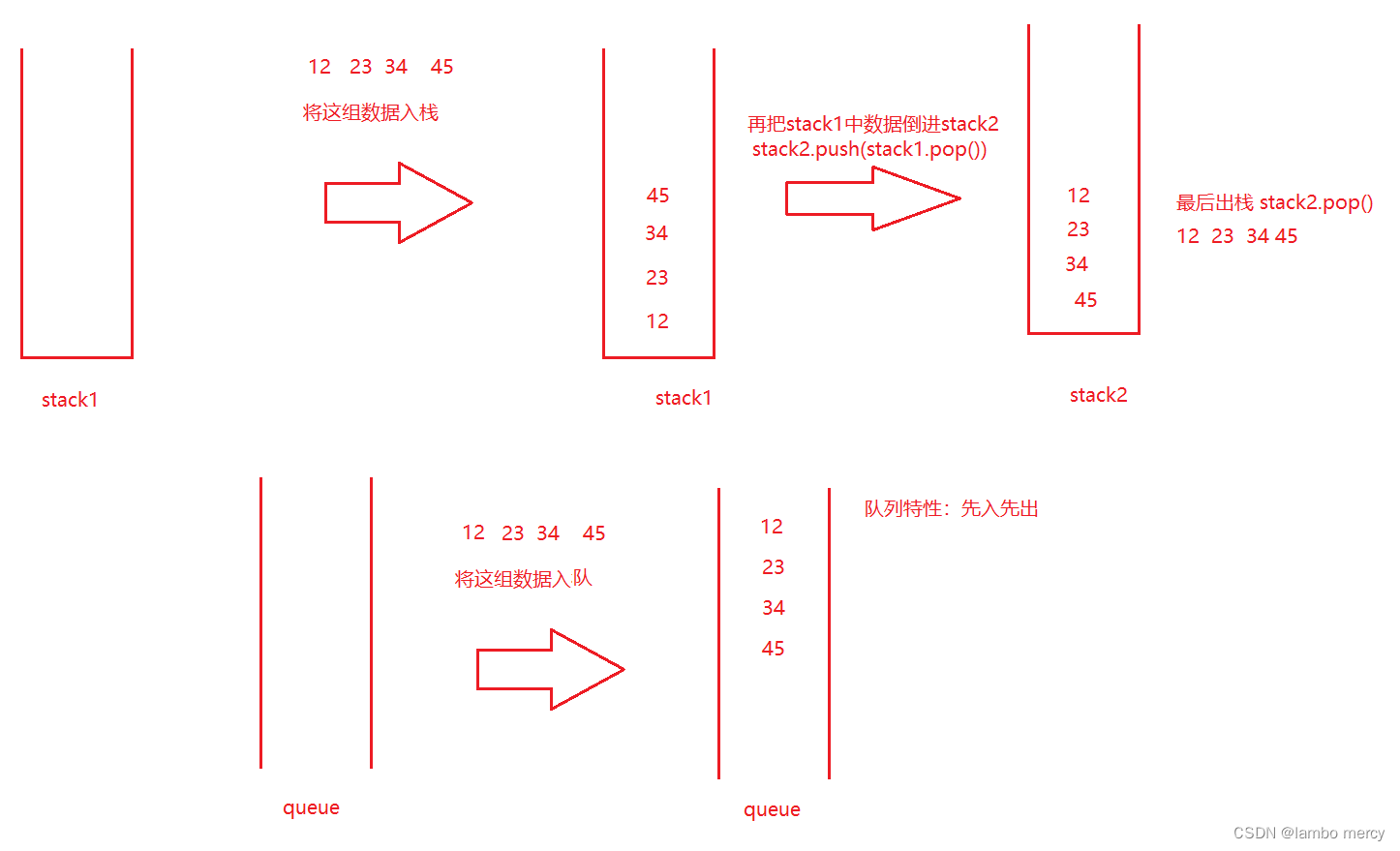
很简单, 栈 的特性是:先进后出。也就是说第一个入栈的数据,将是最后一个出栈,
我们利用两个栈来实现这题。
代码如下
class MyQueue {Stack<Integer> stack1;Stack<Integer> stack2;public MyQueue() {stack1 = new Stack<>();stack2 = new Stack<>();}public void push(int x) {stack1.push(x);}public int pop() {if(stack2.isEmpty()){while(!stack1.isEmpty()){stack2.push(stack1.pop());}}return stack2.pop();}public int peek() {// 防止 别人一开始 就调用 peek,所以 peek 也需要 写 stack1 导入 stack2 的程序if(stack2.isEmpty()){while(!stack1.isEmpty()){stack2.push(stack1.pop());}}return stack2.peek();}public boolean empty() {// 如果模拟的队列 将全部数据出队,那么 stack1 和 stack2 都为空return stack1.isEmpty() && stack2.isEmpty();}
}





)

)












