大家好,我是带我去滑雪!
非线性函数拟合是一种用于找到与给定数据点集合最好匹配的非线性函数的过程。非线性函数拟合通常用于以下情况:
- 数据趋势不是线性的:当数据点之间的关系不能用线性方程来表示时,需要使用非线性函数来更好地拟合数据。
- 复杂的数据模式:当数据包含复杂的非线性模式或曲线时,非线性函数拟合可以提供更准确的拟合结果。
- 物理、生物、经济或其他领域的实验数据:许多自然现象和实验数据无法用简单的线性模型来解释,因此需要使用非线性模型。
下面使用遗传算法优化的BP神经网络实现非线性函数拟合:
目录
一、预备知识
(1)什么是遗传算法
(2)拟合函数
二、模型建立
(1)遗传算法优化BP神经网络算法流程
(2)适应度函数
(3)选择操作
(4)交叉
(5) 变异
(6) 遗传算法主函数
(7) 将遗传算法的到的最优个体赋值进BP神经网络
(8)结果分析
一、预备知识
(1)什么是遗传算法
遗传算法(Genetic Algorithm, GA)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。其主要特点是直接对结构对象进行操作,不存在求导和函数连续性的限定;具有内在的隐并行性和更好的全局寻优能力;采用概率化的寻优方法,不需要确定的规则就能自动获取和指导优化的搜索空间,自适应地调整搜索方向。遗传算法以一种群体中的所有个体为对象,并利用随机化技术指导对一个被编码的参数空间进行高效搜索。其中,选择、交叉和变异构成了遗传算法的遗传操作;参数编码、初始群体的设定、适应度函数的设计、遗传操作设计、控制参数设定五个要素组成了遗传算法的核心内容。
- 选择操作:从旧群体中以一定的概率选择个体到新群体中,个体被选中的概率跟适应度值有关,个体适应度值越好,被选择的概率越大。
- 交叉操作:从个体中选择两个个体,通过染色体的交换组合,来产生新的优秀个体。交叉过程为从群体中任选两个染色体,随机选择一点或多点染色体位置进行交换。
- 变异操作:从群体中选择一个个体,选择染色体中的一点进行变异以产生更优秀的个体。
运行参数主要包括群体大小、遗传代数、交叉概率、变异概率 。
(2)拟合函数
本次需要拟合的非线性函数为:
clc,clear,close all
x=-6:0.1:6;
[X,Y]=meshgrid(x);
Z=X.^2+Y.^2;
mesh(X,Y,Z)绘制函数图像为:

二、模型建立
(1)遗传算法优化BP神经网络算法流程
流程分为:BP神经网络结构确定、遗传算法优化、BP神经网络预测。由于拟合函数中有两个输入参数,1个输出参数,所以设置BP神经网络结构为2-5-1,即输入层节点为2,隐含层节点为5,输出层节点为1,总共有2x5+5x1=15个权重,5+1=6个阈值,使用遗传算法个体的编码长度为15+6=21个。从非线性函数中随机得到2000组输入输出数据,随机选择其中1900组作为训练数据,100组作为测试数据。将训练数据预测误差绝对值和作为个体适应度值,个体适应度值越小,该个体越优。
遗传算法参数设置为:种群规模为10,进化次数为50次,交叉概率为0.4,变异概率为0.2。
(2)适应度函数
将训练数据预测误差作为个体适应度值。
function error = fun(x,inputnum,hiddennum,outputnum,net,inputn,outputn)
w1=x(1:inputnum*hiddennum);
B1=x(inputnum*hiddennum+1:inputnum*hiddennum+hiddennum);
w2=x(inputnum*hiddennum+hiddennum+1:inputnum*hiddennum+hiddennum+hiddennum*outputnum);
B2=x(inputnum*hiddennum+hiddennum+hiddennum*outputnum+1:inputnum*hiddennum+hiddennum+hiddennum*outputnum+outputnum);
net.trainParam.epochs=20;
net.trainParam.lr=0.1;
net.trainParam.goal=0.00001;
net.trainParam.show=100;
net.trainParam.showWindow=0;
net.iw{1,1}=reshape(w1,hiddennum,inputnum);
net.lw{2,1}=reshape(w2,outputnum,hiddennum);
net.b{1}=reshape(B1,hiddennum,1);
net.b{2}=B2;
net=train(net,inputn,outputn);an=sim(net,inputn);error=sum(abs(an-outputn));(3)选择操作
选择操作采用轮盘赌法从种群中选择适应度好的个体组成新种群。
function ret=select(individuals,sizepop)
fitness1=10./individuals.fitness;
sumfitness=sum(fitness1);
sumf=fitness1./sumfitness;
index=[];
for i=1:sizepop %转sizepop次轮盘pick=rand;while pick==0 pick=rand; endfor j=1:sizepop pick=pick-sumf(i); if pick<0 index=[index j]; break;endend
end
individuals.chrom=individuals.chrom(index,:);
individuals.fitness=individuals.fitness(index);
ret=individuals;(4)交叉
function ret=Cross(pcross,lenchrom,chrom,sizepop,bound)for i=1:sizepop pick=rand(1,2);while prod(pick)==0pick=rand(1,2);endindex=ceil(pick.*sizepop);pick=rand;while pick==0pick=rand;endif pick>pcrosscontinue;endflag=0;while flag==0pick=rand;while pick==0pick=rand;endpos=ceil(pick.*sum(lenchrom));pick=rand;v1=chrom(index(1),pos);v2=chrom(index(2),pos);chrom(index(1),pos)=pick*v2+(1-pick)*v1;chrom(index(2),pos)=pick*v1+(1-pick)*v2; flag1=test(lenchrom,bound,chrom(index(1),:)); flag2=test(lenchrom,bound,chrom(index(2),:)); if flag1*flag2==0flag=0;else flag=1;end endend
ret=chrom;(5) 变异
function ret=Mutation(pmutation,lenchrom,chrom,sizepop,num,maxgen,bound)for i=1:sizepop pick=rand;while pick==0pick=rand;endindex=ceil(pick*sizepop);pick=rand;if pick>pmutationcontinue;endflag=0;while flag==0pick=rand;while pick==0 pick=rand;endpos=ceil(pick*sum(lenchrom)); pick=rand;fg=(rand*(1-num/maxgen))^2;if pick>0.5chrom(i,pos)=chrom(i,pos)+(bound(pos,2)-chrom(i,pos))*fg;elsechrom(i,pos)=chrom(i,pos)-(chrom(i,pos)-bound(pos,1))*fg;end flag=test(lenchrom,bound,chrom(i,:)); end
end
ret=chrom;(6) 遗传算法主函数
clc
clear
load data input outputinputnum=2;
hiddennum=5;
outputnum=1;input_train=input(1:1900,:)';
input_test=input(1901:2000,:)';
output_train=output(1:1900)';
output_test=output(1901:2000)';[inputn,inputps]=mapminmax(input_train);
[outputn,outputps]=mapminmax(output_train);net=newff(inputn,outputn,hiddennum);maxgen=20;
pcross=[0.2];
pmutation=[0.1];numsum=inputnum*hiddennum+hiddennum+hiddennum*outputnum+outputnum;lenchrom=ones(1,numsum);
bound=[-3*ones(numsum,1) 3*ones(numsum,1)]; individuals=struct('fitness',zeros(1,sizepop), 'chrom',[]);
avgfitness=[];
bestfitness=[];
bestchrom=[];for i=1:sizepopindividuals.chrom(i,:)=Code(lenchrom,bound); x=individuals.chrom(i,:);individuals.fitness(i)=fun(x,inputnum,hiddennum,outputnum,net,inputn,outputn);
end
FitRecord=[];[bestfitness bestindex]=min(individuals.fitness);
bestchrom=individuals.chrom(bestindex,:);
avgfitness=sum(individuals.fitness)/sizepop;
trace=[avgfitness bestfitness]; for i=1:maxgeniindividuals=Select(individuals,sizepop); avgfitness=sum(individuals.fitness)/sizepop;individuals.chrom=Cross(pcross,lenchrom,individuals.chrom,sizepop,bound);individuals.chrom=Mutation(pmutation,lenchrom,individuals.chrom,sizepop,i,maxgen,bound);for j=1:sizepopx=individuals.chrom(j,:); individuals.fitness(j)=fun(x,inputnum,hiddennum,outputnum,net,inputn,outputn); end[newbestfitness,newbestindex]=min(individuals.fitness);[worestfitness,worestindex]=max(individuals.fitness);if bestfitness>newbestfitnessbestfitness=newbestfitness;bestchrom=individuals.chrom(newbestindex,:);endindividuals.chrom(worestindex,:)=bestchrom;individuals.fitness(worestindex)=bestfitness;avgfitness=sum(individuals.fitness)/sizepop;trace=[trace;avgfitness bestfitness];FitRecord=[FitRecord;individuals.fitness];
end(7) 将遗传算法的到的最优个体赋值进BP神经网络
w1=x(1:inputnum*hiddennum);
B1=x(inputnum*hiddennum+1:inputnum*hiddennum+hiddennum);
w2=x(inputnum*hiddennum+hiddennum+1:inputnum*hiddennum+hiddennum+hiddennum*outputnum);
B2=x(inputnum*hiddennum+hiddennum+hiddennum*outputnum+1:inputnum*hiddennum+hiddennum+hiddennum*outputnum+outputnum);net.iw{1,1}=reshape(w1,hiddennum,inputnum);
net.lw{2,1}=reshape(w2,outputnum,hiddennum);
net.b{1}=reshape(B1,hiddennum,1);
net.b{2}=B2;net.trainParam.epochs=100;
net.trainParam.lr=0.1;[net,per2]=train(net,inputn,outputn);inputn_test=mapminmax('apply',input_test,inputps);
an=sim(net,inputn_test);
test_simu=mapminmax('reverse',an,outputps);
error=test_simu-output_test;(8)结果分析
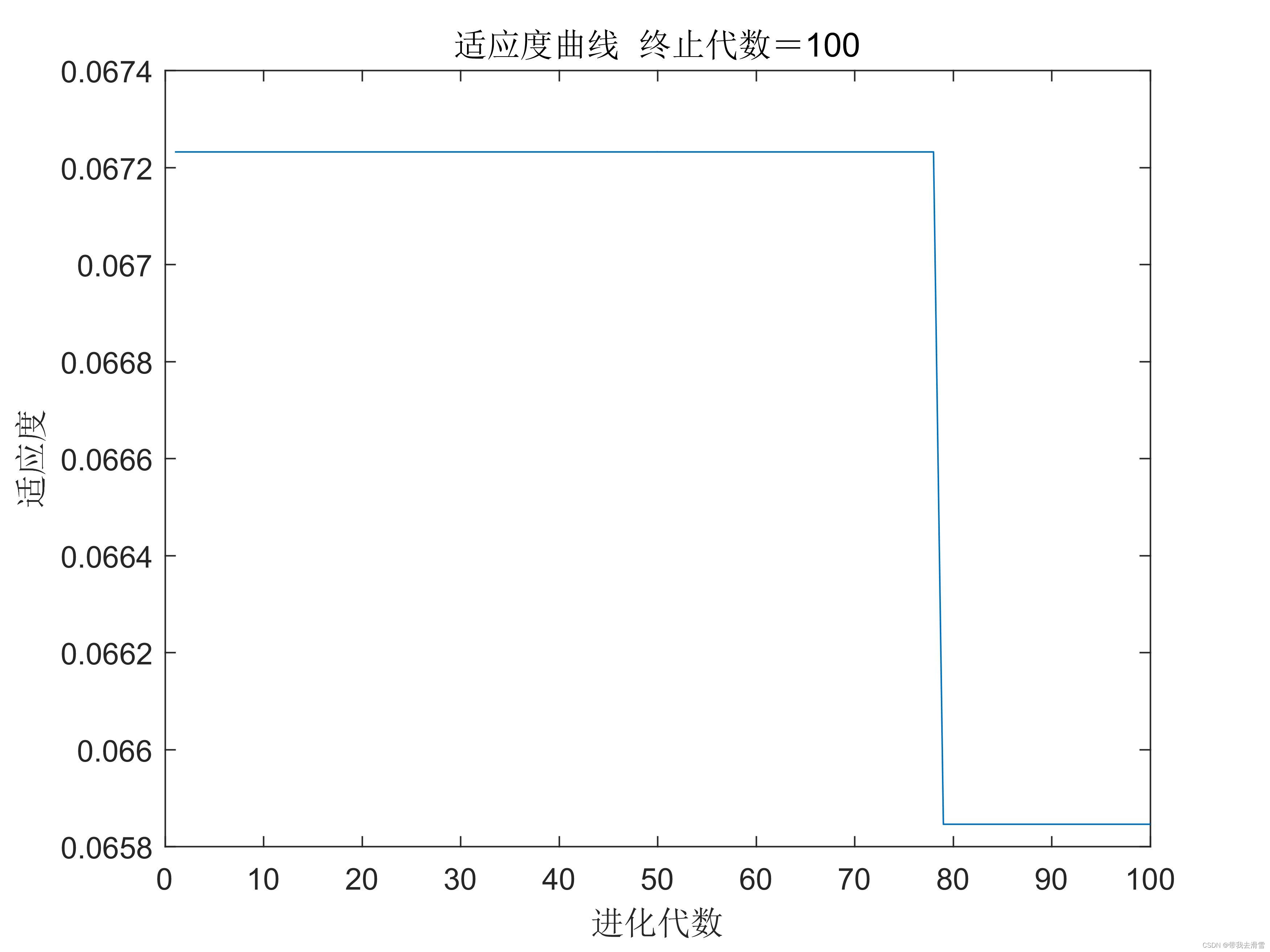
绘制遗传算法优化过程中最优个体适应度值变化图:
figure(1)
[r c]=size(trace);
plot([1:r]',trace(:,2),'b--');
title(['适应度曲线 ' '终止代数=' num2str(maxgen)]);
xlabel('进化代数');ylabel('适应度');
legend('平均适应度','最佳适应度');输出结果:
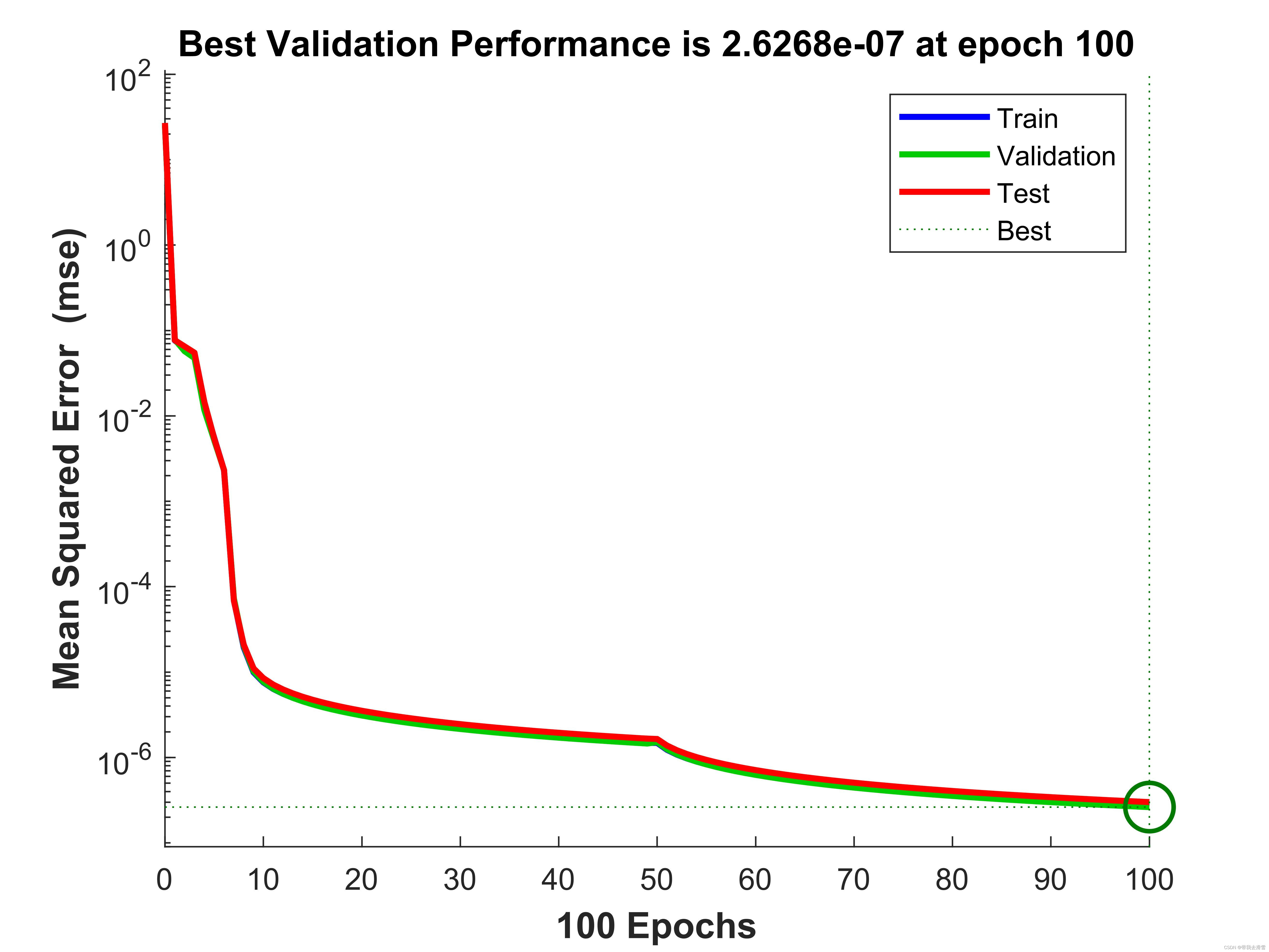
模型的均方误差为2.2628x10的负7次方,什么模型的效果还可以。
更多优质内容持续发布中,请移步主页查看。
点赞+关注,下次不迷路!




的实现过程及其原理【核心知识点精讲】(22))

)




)
)





![[CISCN 2023 初赛]go_session](http://pic.xiahunao.cn/[CISCN 2023 初赛]go_session)
