笔记为自我总结整理的学习笔记,若有错误欢迎指出哟~
深度学习专栏链接:
http://t.csdnimg.cn/dscW7
pytorch——Autograd
- Autograd简介
- requires_grad
- 计算图
- 没有梯度追踪的张量ensor.data 、tensor.detach()
- 非叶子节点的梯度
- 计算图特点总结
- 利用Autograd实现线性回归
Autograd简介
autograd是PyTorch中的自动微分引擎,它是PyTorch的核心组件之一。autograd提供了一种用于计算梯度的机制,使得神经网络的训练变得更加简洁和高效。
在深度学习中,梯度是优化算法(如反向传播)的关键部分。通过计算输入变量相对于输出变量的梯度,可以确定如何更新模型的参数以最小化损失函数。
autograd的工作原理是跟踪在张量上进行的所有操作,并构建一个有向无环图(DAG),称为计算图。这个计算图记录了张量之间的依赖关系,以及每个操作的梯度函数。当向前传播时,autograd会自动执行所需的计算并保存中间结果。当调用.backward()函数时,autograd会根据计算图自动计算梯度,并将梯度存储在每个张量的.grad属性中。
使用autograd非常简单。只需将需要进行梯度计算的张量设置为requires_grad=True,然后执行前向传播和反向传播操作即可。例如:
import torch as tx = t.tensor([2.0], requires_grad=True)
y = x**2 + 3*x + 1y.backward()print(x.grad) # 输出:tensor([7.])
在上述代码中,首先创建了一个张量 x,并设置了 requires_grad=True,表示想要计算关于 x 的梯度。然后,定义了一个计算图 y,通过对 x 进行一系列操作得到结果 y。最后,调用 .backward() 函数执行反向传播,并通过 x.grad 获取计算得到的梯度。
autograd的存在使得训练神经网络变得更加方便,无需手动计算和更新梯度。同时,它也为实现更复杂的计算图和自定义的梯度函数提供了灵活性和扩展性。
requires_grad
requires_grad是PyTorch中张量的一个属性,用于指定是否需要计算该张量的梯度。如果需要计算梯度,则需将其设置为True,否则设置为False。默认情况下,该属性值为False。
在深度学习中,通常需要对模型的参数进行优化,因此需要计算这些参数的梯度。通过将参数张量的requires_grad属性设置为True,可以告诉PyTorch跟踪其计算并计算梯度。除了参数张量之外,还可以将其他需要计算梯度的张量设置为requires_grad=True,以便计算它们的梯度。
需要注意的是,如果张量的requires_grad属性为True,则计算成本会略微增加,因为PyTorch需要跟踪该张量的计算并计算其梯度。因此,对于不需要计算梯度的张量,最好将其requires_grad属性设置为False,以减少计算成本。
计算图
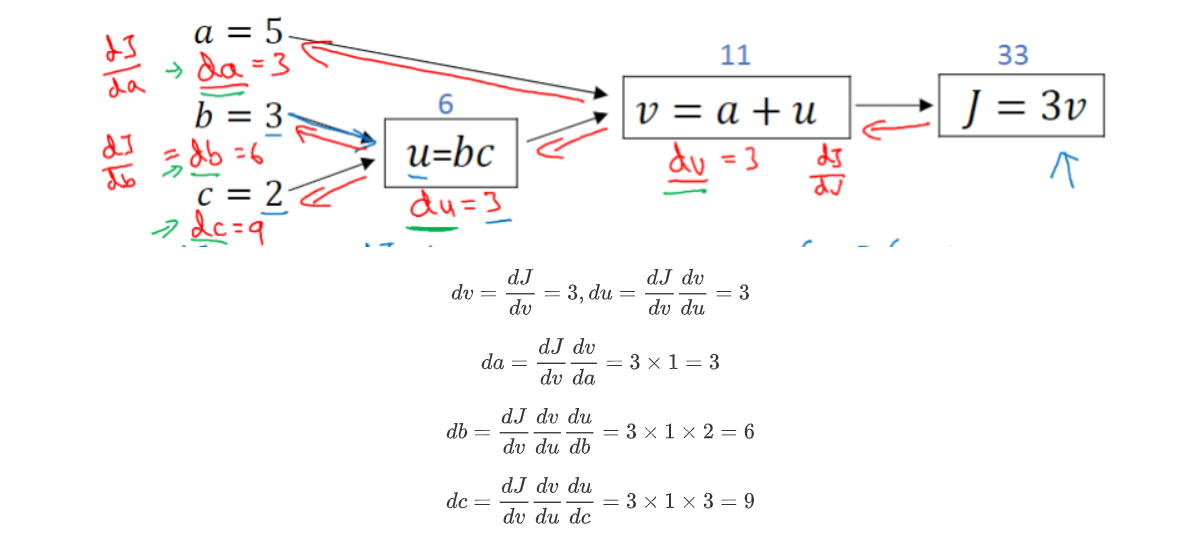
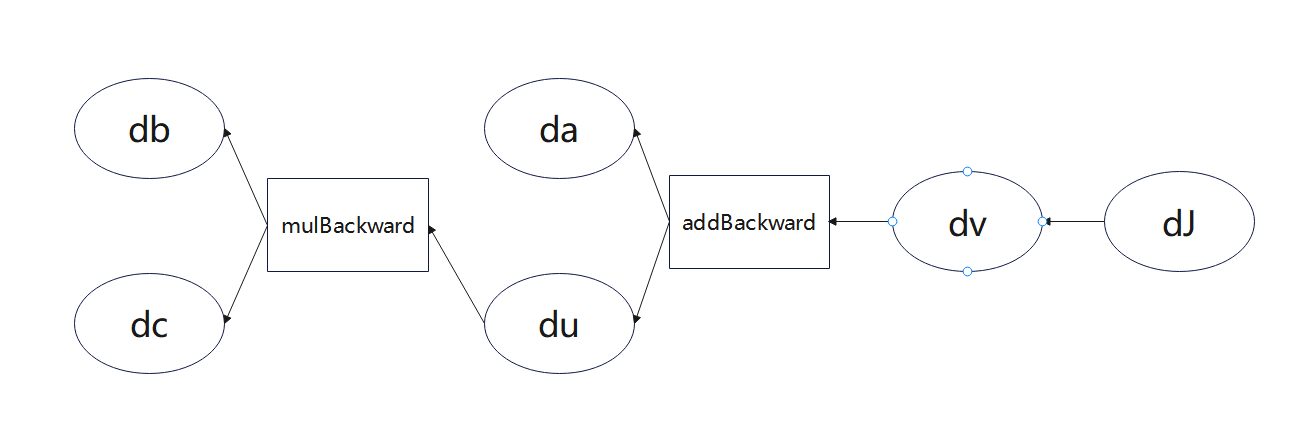
PyTorch中autograd的底层采用了计算图,计算图是一种特殊的有向无环图(DAG),用于记录算子与变量之间的关系。一般用矩形表示算子,椭圆形表示变量。其计算图如图所示,图中MUL,ADD都是算子, a \textbf{a} a, b \textbf{b} b, c \textbf{c} c即变量。
没有梯度追踪的张量ensor.data 、tensor.detach()
tensor.data和tensor.detach()都可以用于获取一个没有梯度追踪的张量副本,但它们之间有一些细微的区别。
tensor.data是一个属性,用于返回一个与原始张量共享数据存储的新张量,但不会共享梯度信息。这意味着对返回的张量进行操作不会影响到原始张量的梯度。然而,如果在计算图中使用了这个新的张量,梯度仍会通过原始张量进行传播。
以下是一个示例说明:
import torchx = torch.tensor([2.0], requires_grad=True)
y = x**2 + 3*x + 1z = y.data
z *= 2 # 操作z不会影响到y的梯度y.backward()print(x.grad) # 输出:tensor([7.])
在上述代码中,我们首先创建了一个张量x,并设置了requires_grad=True,表示我们希望计算关于x的梯度。然后,我们定义了一个计算图y,并将其赋值给z,通过操作z不会影响到y的梯度。最后,我们调用.backward()方法计算相对于x的梯度,并将梯度存储在x.grad属性中。
tensor.detach()是一个函数,用于返回一个新的张量,与原始张量具有相同的数据内容,但不会共享梯度信息。与tensor.data不同的是,tensor.detach()可以应用于任何张量,而不仅限于具有requires_grad=True的张量。
以下是使用tensor.detach()的示例:
import torchx = torch.tensor([2.0], requires_grad=True)
y = x**2 + 3*x + 1z = y.detach()
z *= 2 # 操作z不会影响到y的梯度y.backward()print(x.grad) # 输出:tensor([7.])
在上述代码中,我们执行了与前面示例相同的操作,将y赋值给z,并通过操作z不会影响到y的梯度。最后,我们调用.backward()方法计算相对于x的梯度,并将梯度存储在x.grad属性中。
总结来说,tensor.data和tensor.detach()都可以用于获取一个没有梯度追踪的张量副本,但tensor.detach()更加通用,可应用于任何张量。
非叶子节点的梯度
在反向传播过程中,非叶子节点的梯度默认情况下是被清空的。
1.使用.retain_grad()方法:在创建张量时,可以使用.retain_grad()方法显式指定要保留梯度信息。然后,在反向传播后,可以访问这些非叶子节点的梯度。
import torchx = torch.tensor([2.0], requires_grad=True)
y = x**2 + 3*x + 1y.retain_grad()z = y.mean()z.backward()grad_y = y.gradprint(grad_y) # 输出:tensor([1.])2.第二种方法:使用hook。hook是一个函数,输入是梯度,不应该有返回值
import torchdef variable_hook(grad):print('y的梯度:',grad)x = torch.ones(3, requires_grad=True)
w = torch.rand(3, requires_grad=True)
y = x * w
# 注册hook
hook_handle = y.register_hook(variable_hook)
z = y.sum()
z.backward()# 除非你每次都要用hook,否则用完之后记得移除hook
hook_handle.remove()
计算图特点总结
在PyTorch中,计算图是一种用于表示计算过程的数据结构。
动态计算图:PyTorch使用动态计算图,这意味着计算图是根据实际执行流程动态构建的。这使得在每次前向传播过程中可以根据输入数据的不同而灵活地构建计算图。
自动微分:PyTorch的计算图不仅用于表示计算过程,还支持自动微分。通过计算图,PyTorch可以自动计算梯度,无需手动编写反向传播算法。这大大简化了深度学习模型的训练过程。
基于节点的表示:计算图由一系列节点(Node)和边(Edge)组成,其中节点表示操作(如张量运算)或变量(如权重),边表示数据的流动。每个节点都包含了前向计算和反向传播所需的信息。
叶子节点和非叶子节点:在计算图中,叶子节点是没有输入边的节点,通常表示输入数据或需要求梯度的变量。非叶子节点是具有输入边的节点,表示计算操作。在反向传播过程中,默认情况下,只有叶子节点的梯度会被计算和保留,非叶子节点的梯度会被清空。
延迟执行:PyTorch中的计算图是按需执行的。也就是说,在前向传播过程中,只有实际需要计算的节点才会被执行,不需要计算的节点会被跳过。这种延迟执行的方式提高了效率,尤其对于大型模型和复杂计算图来说。
计算图优化:PyTorch内部使用了一些优化技术来提高计算图的效率。例如,通过共享内存缓存中间结果,避免重复计算;通过融合多个操作为一个操作,减少计算和内存开销等。这些优化技术可以提高计算速度,并减少内存占用。
利用Autograd实现线性回归
【深度学习】pytorch——线性回归:http://t.csdnimg.cn/7KsP3
上一篇文章为手动计算梯度,这里来利用Autograd实现自动计算梯度
import torch as t
%matplotlib inline
from matplotlib import pyplot as plt
from IPython import display
import numpy as np# 设置随机数种子,保证在不同电脑上运行时下面的输出一致
t.manual_seed(1000) def get_fake_data(batch_size=8):''' 产生随机数据:y=x*2+3,加上了一些噪声'''x = t.rand(batch_size, 1, device=device) * 5y = x * 2 + 3 + t.randn(batch_size, 1, device=device)return x, y# 随机初始化参数
w = t.rand(1,1, requires_grad=True)
b = t.zeros(1,1, requires_grad=True)
losses = np.zeros(500)lr =0.02 # 学习率for ii in range(500):x, y = get_fake_data(batch_size=4)# forward:计算lossy_pred = x.mm(w) + b.expand_as(y) loss = 0.5 * (y_pred - y) ** 2 # 均方误差loss = loss.sum()losses[ii] = loss.item()# backward:自动计算梯度loss.backward()# 更新参数w.data.sub_(lr * w.grad.data)b.data.sub_(lr * b.grad.data)# 梯度清零w.grad.data.zero_()b.grad.data.zero_()if ii%50 ==0:# 画图display.clear_output(wait=True)x = t.arange(0, 6).view(-1, 1).float()y = x.mm(w.data) + b.data.expand_as(x)plt.plot(x.numpy(), y.numpy(),color='b') # predictedx2, y2 = get_fake_data(batch_size=100) plt.scatter(x2.numpy(), y2.numpy(),color='r') # true dataplt.xlim(0,5)plt.ylim(0,15) plt.show()plt.pause(0.5)print('w: ', w.item(), 'b: ', b.item())
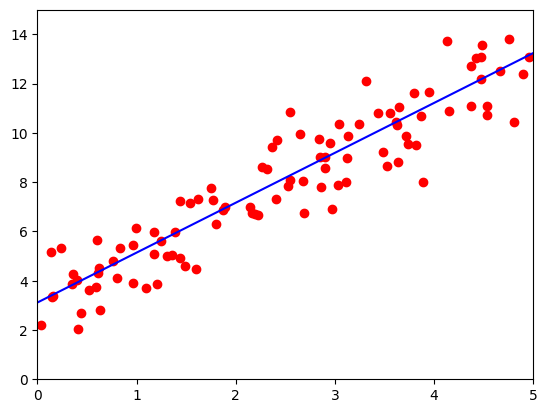
w: 2.036161422729492 b: 3.095750331878662
以下是代码的主要步骤:
-
定义了一个
get_fake_data函数,用于生成带有噪声的随机数据,数据的真实关系为 y = x ∗ 2 + 3 y=x*2+3 y=x∗2+3。 -
初始化参数
w和b,并设置requires_grad=True以便自动计算梯度。 -
进行500轮训练,每轮训练包括以下步骤:
- 从
get_fake_data函数中获取一个小批量的训练数据。 - 前向传播:计算模型的预测值
y_pred,即 x x x与参数w和b的线性组合。 - 计算均方误差损失函数。
- 反向传播:自动计算参数
w和b的梯度。 - 更新参数:通过梯度下降法更新参数
w和b。 - 清零梯度:将参数的梯度置零,以便下一轮计算梯度。
- 每50轮训练,可视化当前模型的预测结果和真实数据的散点图。
- 从
-
训练结束后,打印出最终学得的参数
w和b。
plt.plot(losses)
plt.ylim(0,50)
实现了对损失函数随训练轮数变化的可视化。losses是一个长度为500的数组,记录了每一轮训练后的损失函数值。plt.plot(losses)会将这些损失函数值随轮数的变化连成一条曲线,可以直观地看到模型在训练过程中损失函数的下降趋势。
plt.ylim(0,50)用于设置y轴的范围,保证曲线能够完整显示在图像中。




CMocka-单元测试框架使用)








)





