🚀 作者:阿辉不一般
🚀 你说呢:生活本来沉闷,但跑起来就有风
🚀 专栏:爱上C语言
🚀作图工具:draw.io(免费开源的作图网站)
如果觉得文章对你有帮助的话,还请点赞,关注,收藏支持博主,如有不足还请指点,博主及时改正,感谢大家支持!!!
文章目录
- 🚀前言
- 🚀什么是函数递归?
- 🚀函数递归的必要条件
- 🚀 用递归求n的阶乘
- 🚀青蛙跳台阶问题(斐波那契数列)
- 🚀什么是栈溢出?
🚀前言
大家好啊😉!今天阿辉将为大家介绍C语言中的函数的递归,✍包括什么是函数递归,函数递归的必要条件,青蛙跳台阶问题(斐波那契数列)以及栈溢出问题,内容干货满满😋,接下来就跟着阿辉一起学习吧👊
🚀什么是函数递归?
函数递归:简单来说就是函数自己调自己。
递归做为一种算法在程序设计语言中广泛应用。 一个过程或函数在其定义或说明
中有直接或间接调用自身的一种方法,它通常把一个大型复杂的问题层层转化为一个与
原问题相似的规模较小的问题来求解递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算,大大地减少了
程序、的代码量。递归的能力在于用有限的语句来定义对象的无限集合。一般来说,递
归需要、有边界条件、递归前进段和递归返回段。当边界条件不满足时,递归前进;当
边界条件满足时,递归返回。
🚀函数递归的必要条件
- 递归存在限制条件,当满足限制条件时函数便不再不在递归下去了
- 每一次递归后都会逐渐接近这个限制条件
这两个条件是必要的,否则将陷入死递归
我们来看个例子👇
#include<stdio.h>int main()
{printf("hallo c !\n");main();return 0;
}
上面这段代码你在VS上调试的话就会报错
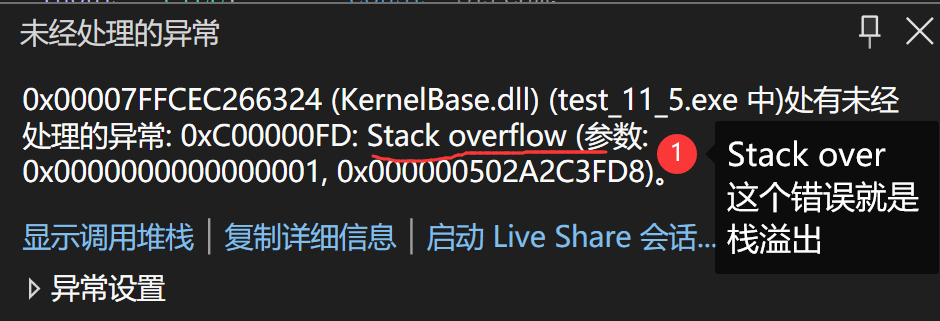
栈溢出是什么?别急后面会讲,我们接着看👊
🚀 用递归求n的阶乘
5! = 5*4*3*2*1 4! = 4*3*2*1
3! = 3*2*1 2! = 2*1
1! = 1 0! = 1
我们看出求 5!可以变成求 5*4!
而4! = 4*3! 3! = 3*2! 2! = 2*1!
以此类推由上图我们把青蛙跳台阶抽象成下面这个模型👇
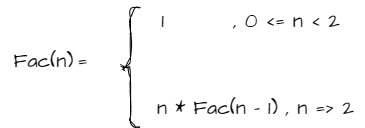
把n的阶乘记作Fac(n)
由上图我们可以写出n的阶乘的函数递归代码
int Fac(int n)
{if (n < 2)return 1;elsereturn n * Fac(n - 1);
}
int main()
{int n = 0;scanf("%d", &n);int a = Fac(n);printf("%d\n", a);return 0;
}
🚀青蛙跳台阶问题(斐波那契数列)
一只青蛙一次可以跳上 1 级台阶,也可以跳上2 级。求该青蛙跳上一个n 级的台阶总共有多少种跳法
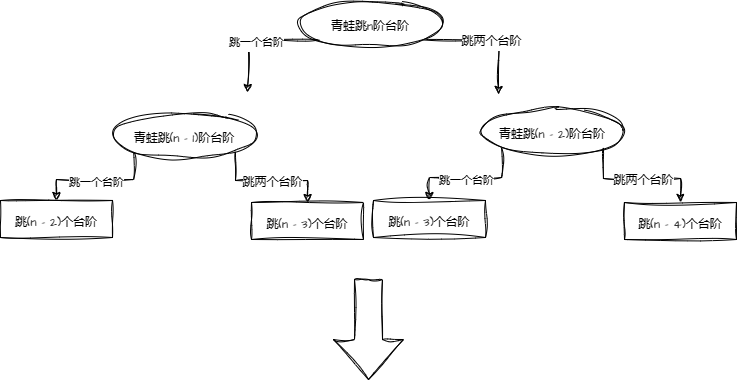
上图我们可知,青蛙跳n次台阶的跳法可以分成:青蛙跳(n - 1)次台阶的跳法加上青蛙跳(n - 2)次台阶的跳法
而青蛙跳(n - 1)次台阶的跳法又可以分成:青蛙跳(n - 2)次台阶的跳法加上青蛙跳(n - 3)次台阶的跳法
…
以此类推由上图我们把青蛙跳台阶抽象成下面这个模型👇
把青蛙跳n次台阶的次数记作Fib(n)
上图其实也就是斐波那契数列得到的方法,只不过斐波那契数列前两个数都是1
由上图我们可以写出青蛙跳台阶的函数递归代码
#include<stdio.h>
int Fib(int n)
{if (n < 3)return n;elsereturn Fib(n - 1) + Fib(n - 2);
}
int main()
{int n = 0;scanf("%d", &n);int a = Fib(n);printf("%d\n", a);return 0;
}
虽然递归能以很少的代码量解决复杂的问题,但是如果递归程度太深,递归次数太多将导致效率低下,甚至栈溢出
上述n的阶乘以及青蛙跳台阶都可以用迭代的方式去写,效率更高,利用的栈内存更小
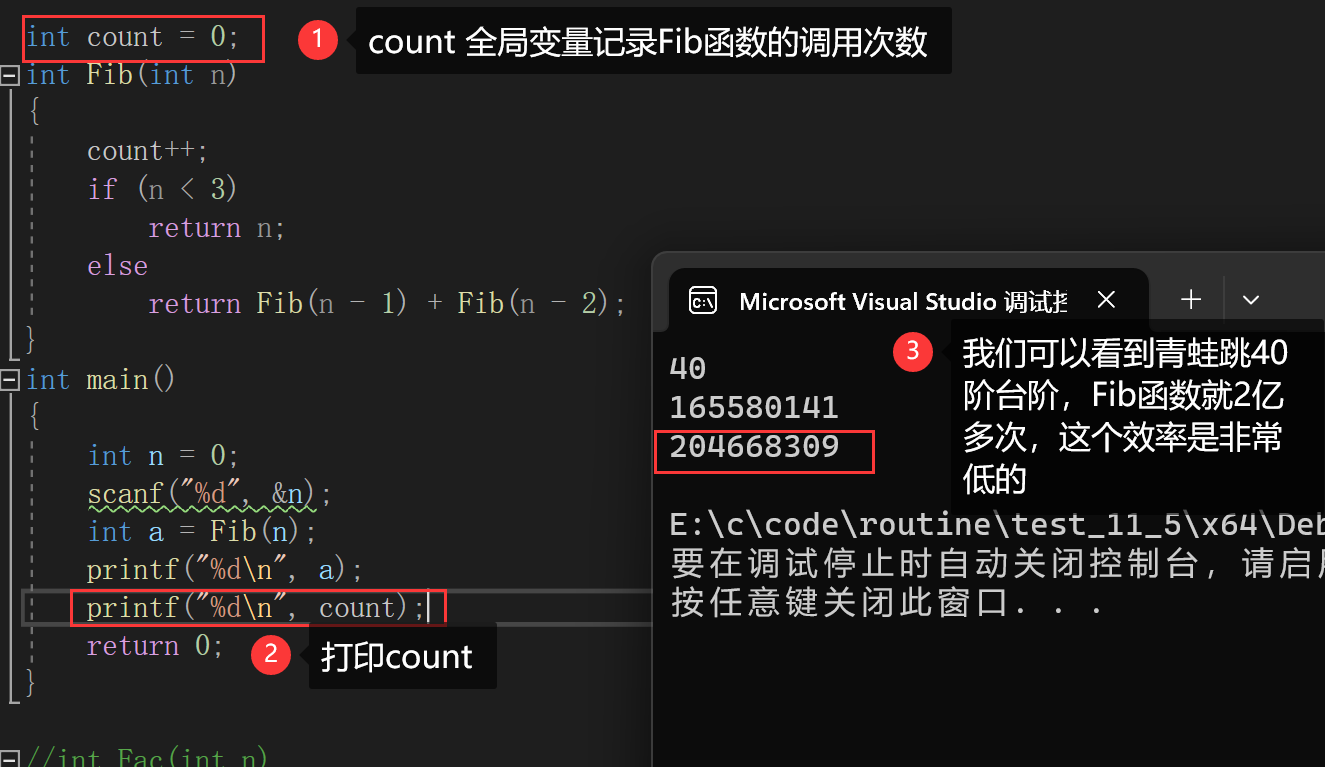
迭代版本n的阶乘以及青蛙跳台阶奉上👊
n的阶乘:
int Fac(int n)
{int i = 0;int ret = 1;for (i = 1; i <= n; i++){ret *= i;}return ret;
}
int main()
{int n = 0;scanf("%d", &n);int a = Fac(n);printf("%d\n", a);return 0;
}
青蛙跳台阶:
int Fib(int n)
{int a = 1;int b = 2;int c = 0;if (n < 3)return n;while (n - 2){c = a + b;a = b;b = c;n--;}return c;
}
int main()
{int n = 0; scanf("%d", &n);int a = Fib(n);printf("%d\n", a);return 0;
}
🚀什么是栈溢出?
栈,又称堆栈,是一种具有一定规则的数据结构,它按照先进后出的原则存储数据,先存的元素放在栈底,后存的元素在栈顶。
栈区存放函数参数以及局部变量等。内存由编译器分配和释放。
那么栈溢出又是什么呢?
栈溢出是指向向栈中写入了超出限定长度的数据,溢出的数据会覆盖栈中其它数据,从而影响程序的运行
而递归每调一次函数都会向栈区申请一块内存空间,如果死递归或者递归层次太深都会导致栈溢出。
SO递归虽好,可不要贪杯啊
到这里,阿辉今天对于C语言函数递归的分享就结束了,希望这篇博客能让大家有所收获, 如果觉得阿辉写得不错的话,记得给个赞呗,你们的支持是我创作的最大动力🌹


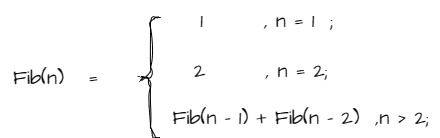






中无法获取RJ45网口eth0或end0的IP地址(没有IPv4的地址无法操作))






 X轴横坐标展示完整整数坐标)


)


