有关python环境！！！

1、python解释器就是 python 3.7.2 之类的。
VSCode 是代码编辑器。
下图的每一个都是可选的python环境，Python 3.8.3（‘base’）是下载在电脑上的python环境（下载miniConda时一直点了next不小心下的），其它的都是下载在miniconda中的虚拟环境。

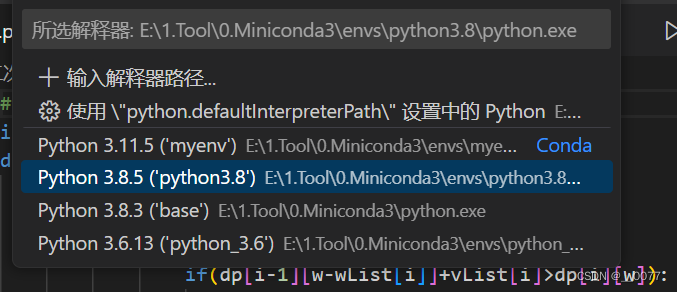
2、其中每一个虚拟环境都在conda\envs 中

然后呢点开任意一个环境，每个单独环境都会有python.exe和各自的Lib和Scripts之类的文件。

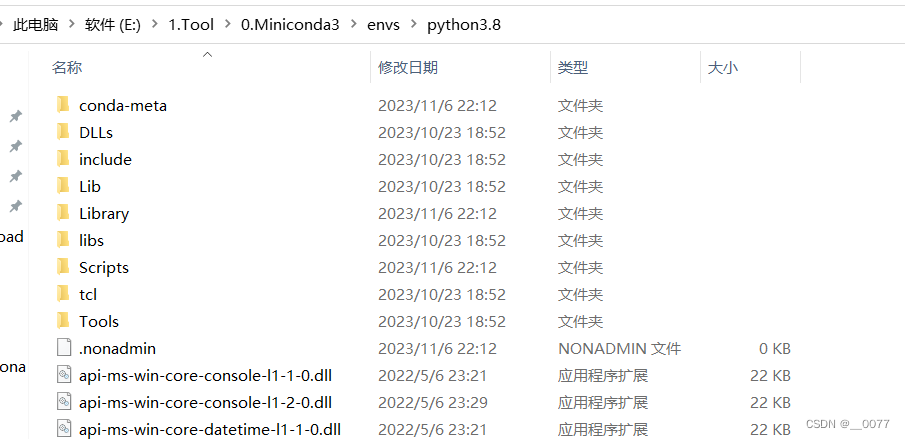
scripts里面放着每次运行.py所需要的文件/python依赖的工具/可执行的文件。
Lib里有通过pip下载的包

python安装后系统会配两个环境变量， 一个是python（编译器），一个是scripts。
scripts里面有pip.exe,pip包是一个.exe文件，.exe都要放到环境变量里才能执行，所以把pip包放到scripts里的话就相当于放到了环境变量里 就可以直接用pip命令管理包