数据结构（四）--队列及面试常考的算法

一、队列介绍

1、定义

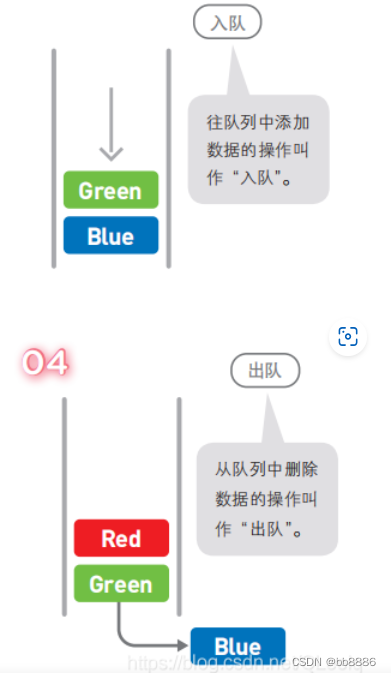
与栈相似，队列是另一种顺序存储元素的线性数据结构。栈与队列的最大差别在于栈是LIFO（后进先出），而队列是FIFO，即先进先出。

2、优缺点及使用场景

优点：先进先出（FIFO）特性、简单明了的接口、任务调度、广度优先搜索（BFS）、消息传递等。

缺点：随机访问困难、固定容量的队列可能导致溢出、不适用于特定的场景、不适用于高并发场景。

使用场景：任务调度、广度优先搜索（BFS）、消息传递等。

3、基本操作

Enqueue()——在队列尾部插入元素

Dequeue()——移除队列头部的元素

isEmpty()——如果队列为空，则返回true

Top()——返回队列的第一个元素

二、常考算法

1、使用队列表示栈

题目：使用队列实现栈的下列操作：

push(x) -- 元素 x 入栈
pop() -- 移除栈顶元素
top() -- 获取栈顶元素
empty() -- 返回栈是否为空

思路：用两个队列que1和que2实现队列的功能，que2其实完全就是一个备份的作用，把que1最后面的元素以外的元素都备份到que2，然后弹出最后面的元素，再把其他元素从que2导回que1。

#include<queue>
#include<iostream>
using namespace std;class StackWithQueue{
public:queue<int> queue1;queue<int> queue2; // 辅助队列，用来备份void push(int data){queue1.push(data);}int pop(){if (queue1.size() == 0) return false;while(queue1.size() > 1){queue2.push(queue1.front());queue1.pop();}int result;result = queue1.front(); // 留下的最后一个元素就是要返回的值queue1.pop();queue1 = queue2;while (!queue2.empty()){ //queue1 = queue2，queue2 = 空 queue2.pop();} return result;}int top(){return queue1.back();}bool empty(){return queue1.empty();}
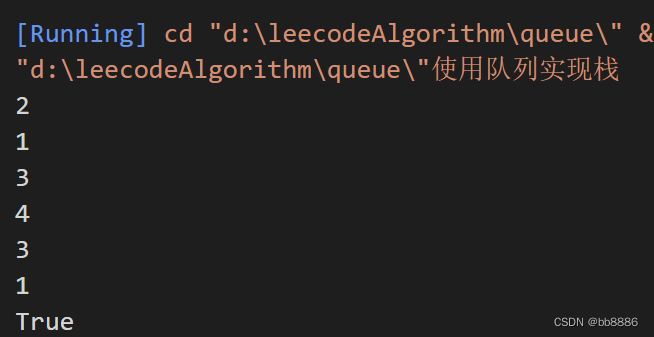
};int main(){StackWithQueue stack;stack.push(1);stack.push(2);cout << stack.pop() << endl;cout << stack.top() << endl;stack.push(3);cout << stack.top() << endl;stack.push(4);cout << stack.pop() << endl;cout << stack.pop() << endl;cout << stack.pop() << endl;if (stack.empty()){cout << "True";}else cout << "False";   
}

时间复杂度: pop为O(n)，其他为O(1)
空间复杂度: O(n)

2、对队列的前k个元素倒序

题目：现有一个整数队列，需要将其前 k 个元素进行逆置，剩余的元素保持原来的顺序。

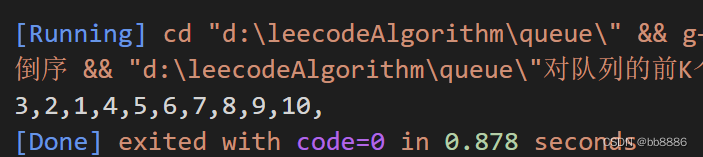
示例：input：[1，2， 3， 4， 5， 6， 7， 8， 9，10]， k = 3;

output：[3, 2, 1, 4, 5, 6, 7, 8, 9, 10]

思路：将前k个元素入栈，再将栈中元素入新队列中，最后将原队列的剩余元素入新队列中。

需要一个新队列用来装结果，需要一个栈用来对元素倒序。（利用栈先进后出，队列先进先出。）

#include<stack>
#include<queue>
#include<iostream>
using namespace std;queue<int> reverse_k_elements(queue<int> queue, int k){stack<int> st;for(int i = 0; i < k; i++){st.push(queue.front());queue.pop();}while(!st.empty()){queue.push(st.top());st.pop();}for(int j = 0; j < queue.size() - k; j++){queue.push(queue.front());queue.pop();}return queue;
}int main(){queue<int> queue, que;int i = 1;while(i < 11){queue.push(i);i++;}que = reverse_k_elements(queue, 3);while(!que.empty()){cout << que.front() << ',';que.pop();}
}

3、使用队列生成从1到n的二进制数

题目：给定值k，打印1到k的二进制数。

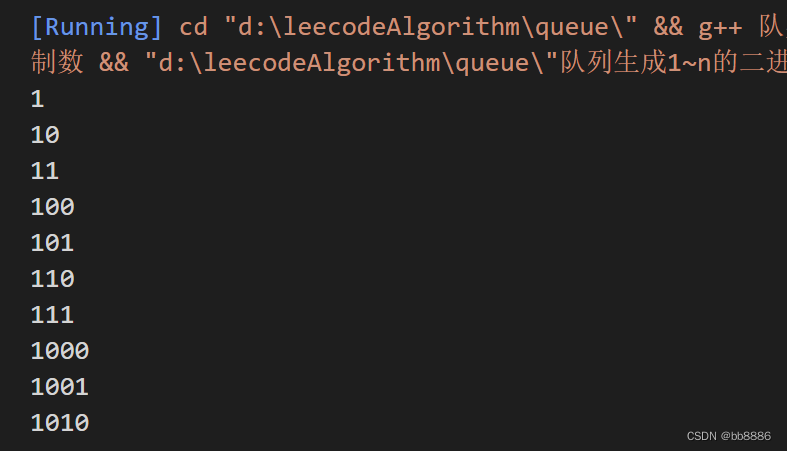
示例：input：5；output：[1, 10, 11, 100, 101]

思路：利用队列的先进先出性质和二进制数的特点来实现。以下是具体的思路：

使用队列存储二进制数-->循环生成下一个二进制数-->重复直到达到n个二进制数。

#include<queue>
#include<iostream>
using namespace std;queue<string> generate_binaray_numbers(int k){queue<string> queue1, queue2;queue1.push("1");string cur;for(int i = 0; i < k; i++){cur = queue1.front();queue1.pop();queue2.push(cur);queue1.push(cur + "0");queue1.push(cur + "1");}return queue2;
}int main(){queue<string> que;que = generate_binaray_numbers(10);while(!que.empty()){cout << que.front()<<endl;que.pop();}return 0;
}