考察知识点:双向链表,小根堆 完整代码在文章末尾
题目
【问题描述】
给定一个长度为 N 的整数数列: A1,A2,...,AN。你要重复以下操作 K 次 : 每次选择数列中最小的整数(如果最小值不止一个,选择最靠前的),将其删除。并把与它相邻的整数加上被删除的数值。
输出 K 次操作后的序列。
【输入格式】
第一行包括两个整数 N 和 K 。
第二行包含 N 个整数,A1,A2,A3......,AN。
【输出格式】
输出N - K 个整数,中间是用一个空格隔开,代表K次操作后的序列。
思路
根据题意可知,这个序列需要大量的删除,我们可以使用链表来实现。
1、定义一个结构体,同时声明一个结构体数组
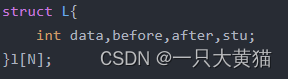
其中data代表这个结构体储存的数据,before代表前驱节点,after代表后继节点,stu代表这个节点是否存在(stu = 1表示未被删除,stu = 0表示已经被删除)。
2、 建一个堆

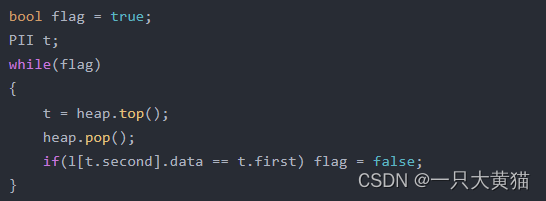
我们将节点的值与节点的索引放入堆中,使用时将节点值最小的节点弹出。(需要判定一下这个节点的值是否已经改变,如果已经改变则不能使用此节点)。
3、输入数据
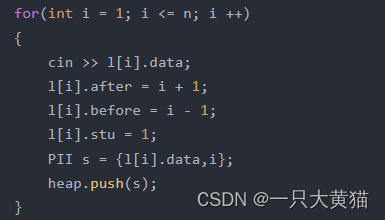
将数据输入,一个节点 i 初始时前驱索引为 i - 1,后继节点索引为 i + 1,状态初始化为1。同时将这个节点放入小根堆中。
4、进行整数删除操作
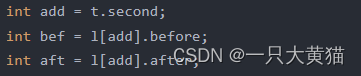
为方便操作使用 add 代表删除节点的索引,bef代表删除节点前驱的索引,aft代表删除节点后继的索引。
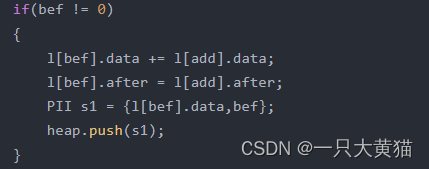
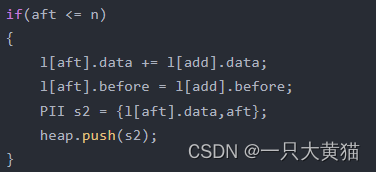
如果前驱节点不为0,则对前驱节点进行更新,将更新后的节点值与索引放入堆中。如果后继节点为≤n,则对后继节点进行更新,将更新后的节点值与索引放入堆中。

add节点已经被删除,将其状态值更新为0,表示该节点已经被删除。接着进行下次循环,直到删除k个节点为止。
5、输出元素
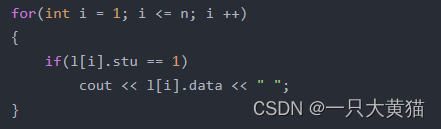
这是最后一步 ,输出元素时要先根据stu值判断该节点是否存在,如果存在则输出,否则不输出。
代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 500010;
typedef pair<int,int> PII;
int n,k;
struct L{int data,before,after,stu;
}l[N];int32_t main()
{cin >> n >> k;priority_queue<PII,vector<PII>,greater<PII>> heap;for(int i = 1; i <= n; i ++){cin >> l[i].data;l[i].after = i + 1;l[i].before = i - 1;l[i].stu = 1;PII s = {l[i].data,i};heap.push(s);}while(k --){bool flag = true;PII t;while(flag){t = heap.top();heap.pop();if(l[t.second].data == t.first) flag = false;}int add = t.second;int bef = l[add].before;int aft = l[add].after;if(bef != 0){l[bef].data += l[add].data;l[bef].after = l[add].after;PII s1 = {l[bef].data,bef};heap.push(s1);}if(aft <= n){l[aft].data += l[add].data;l[aft].before = l[add].before;PII s2 = {l[aft].data,aft};heap.push(s2);}l[add].stu = 0;}for(int i = 1; i <= n; i ++){if(l[i].stu == 1)cout << l[i].data << " ";}return 0;
}


)


)




)
)







