题目
给定3个参数，N，M，K
怪兽有N滴血，等着英雄来砍自己
英雄每一次打击，都会让怪兽流失[0~M]的血量
到底流失多少？每一次在[0~M]上等概率的获得一个值
求K次打击之后，英雄把怪兽砍死的概率。

暴力递归
先确定好暴力递归的尝试方法，并根据方法确定base case。
已知参数是 N：怪兽血量 M：每次等概率砍0 ~ M滴血 K：砍K次。
所以如果暴力递归方法返回在hp滴血情况下，砍times次，每次砍0 ~ M滴血。能将怪兽砍死的方法数。
其中hp：剩余血量 。 tmies：剩余砍的次数。M固定不变。

代码
递归方法就如上面所描述的递归方法进行的尝试，每次砍都等概率掉 0 ~ M滴血（for循环表示），每次掉血后，继续相加递归（次数 times - 1, hp - i 为剩余血量），砍当前砍掉 i 滴血后，能砍死怪兽的方法。
base case : 当次数为0时，如果hp <= 0 ，则return 1，证明怪兽gg，否则返回0，证明当前情况下没砍死怪兽。
需要注意的是，times不为0，但是怪兽 hp <= 0 的情况。
比如说：怪兽hp = 3 。times = 4 还可砍击4次，每次掉 0 ~ 5滴血。
可能我第一刀的时候就砍了5滴血。剩下的3次无论怎么砍，都会成功，怪兽都已经是GG的状态。
此时，就运用到了之前我们所说的“剪枝”的优化技巧。
剩下的几刀都没有必要再进行递归方法向下调用。但是每次 0 ~ M滴血，就是一个M + 1的展开情况，剩余 times = 3。
直接可求得剩余击杀怪兽的方法数 = Math.pow(M + 1, times);

 public static double right(int N, int M, int K) {if (N < 1 || M < 1 || K < 1) {return 0;}//砍怪兽的总方法数：每次都是 0 ~ M滴血，所以是 M + 1的展开，能砍K次。double all = Math.pow(M + 1, K);//击杀怪兽的方法数。double kill = (double) process(K, M, N);return kill / all;}public static double process(int times, int M, int hp) {//如果剩余次数为0，此时剩余血量 <= 0,代表把怪兽砍死，return 1，否则return 0if (times == 0) {return hp <= 0 ? 1 : 0;}//如果在次数用没之前就已经将怪兽砍死，那么直接returnif (hp <= 0) {return Math.pow(M + 1, times);}int ways = 0;//否则，等概率的砍，每一刀砍的范围 0 ~ M。每砍一刀，次数 - 1。for (int i = 0; i <= M; i++) {ways += process(times - 1, M, hp - i);}return ways;}

动态规划
根据上面暴力递归的代码可以看出，可变参数为 hp：怪兽剩余血量 。 times：剩余砍击次数。又因为hp和times都可以到达0。所以可以确定dp表是一个二维数组，以及范围是dp[K + 1][N + 1]。（K，N为题意所给的血量和次数）。
根据暴力递归的base case，当次数为0时，hp如果为0，则return 1。所以可以确定dp[0][0] = 1

 if (times == 0) {return hp <= 0 ? 1 : 0;}

根据这行base case，也可以确定，dp[0][hp] = Math.pow(M + 1, times);。

if (hp <= 0) {return Math.pow(M + 1, times);
}

其余代码照搬暴力递归即可。

完整代码
遍历过程中，hp会有负数的可能，需要注意并进行判断。因为dp表大小是dp[K + 1][N + 1]，此时如果要考虑负数的因素就要扩大N + 1的返回，增加判断，很麻烦。
所以要对hp - i 进行判断， 如果 hp - i >= 0 则从dp表中取。如果 hp - i < 0。则直接从我们的公式 Math.pow(M + 1, times - 1);中取，times - 1是因为当前第times次砍击砍下来后hp - i < 0，剩余times - 1次肯定就是成功的情况。

public static double dp(int N, int M, int K) {if (N < 1 || M < 1 || K < 1) {return 0;}double all = Math.pow(M + 1, K);int[][] dp = new int[K + 1][N + 1];dp[0][0] = 1;for (int times = 1; times <= K; times++) {dp[times][0] = (int) Math.pow(M + 1, times);for (int hp = 1; hp <= N; hp++) {int ways = 0;for (int i = 0; i <= M; i++) {if (hp - i >= 0) {ways += dp[times - 1][hp - i];} else {ways += (int) Math.pow(M + 1, times - 1);}}dp[times][hp] = ways;}}return (double)((double)dp[K][N] / (double)all);}

再次优化
可以看到，动态规划的过程中出现了枚举行为（for循环 0 ~ M滴血），所以如果找到dp表中每个格子间的依赖关系，那么还有进一步的优化空间。
以下图为例：假设，当前times = 2 还剩2次机会，hp = 3 剩余3滴血，M = 3 每次等概率掉 0 ~ 3滴血。
根据暴力递归中依赖关系是 times - 1，hp - i ，i = 0 ~ 3，所以想要求得dp[2][3]格子 √ 处的值需要依赖dp[1,0] ~ dp[1,4]四个格子的累加。

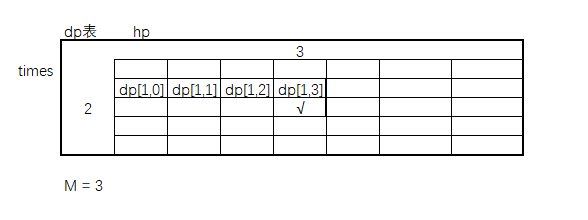
求√’处的值，hp = 4，依然是剩余2次机会，每次 0 ~ 3，依赖的就是dp[1,1] ~ dp[1][4]的值，那此时如果用 √ + dp[1][4] - dp[1][0]，是不是就省去了再求dp[1][1] ~ dp[1][3]的过程。
我们将此过程抽象化一下，就是优化后的代码。

优化代码
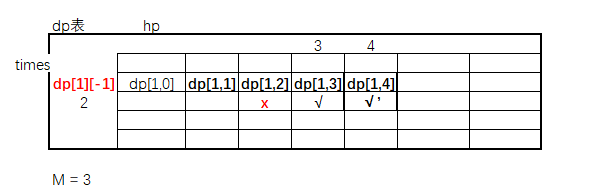
同样要考虑hp负数的问题，如果hp为负数，则前面的也要减掉。
如图：求 √ 位置时，依赖的X已经越界了，那么此时，利用公式Math.pow(M + 1, times - 1);减掉前面的位置。

 public static double bestDP(int N, int M, int K) {if (N < 1 || M < 1 || K < 1) {return 0;}double all = Math.pow(M + 1, K);int[][] dp = new int[K + 1][N + 1];dp[0][0] = 1;for (int times = 1; times <= K; times++) {dp[times][0] = (int) Math.pow(M + 1, times);for (int hp = 1; hp <= N; hp++) {dp[times][hp] = dp[times][hp - 1] + dp[times - 1][hp];if (hp - M - 1 <= 0) {dp[times][hp] -= Math.pow(M + 1, times - 1);} else {dp[times][hp] -= dp[times - 1][hp - M - 1];}}}return (double) ((double) (dp[K][N]) / all);}