本文属于「征服LeetCode」系列文章之一，这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁，本系列将至少持续到刷完所有无锁题之日为止；由于LeetCode还在不断地创建新题，本系列的终止日期可能是永远。在这一系列刷题文章中，我不仅会讲解多种解题思路及其优化，还会用多种编程语言实现题解，涉及到通用解法时更将归纳总结出相应的算法模板。

为了方便在PC上运行调试、分享代码文件，我还建立了相关的仓库：https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中，你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等，还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解，还可以一同分享给他人。

由于本系列文章的内容随时可能发生更新变动，欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。

给你一个整数 n ，表示有 n 节课，课程编号从 1 到 n 。同时给你一个二维整数数组 relations ，其中 relations[j] = [prevCoursej, nextCoursej] ，表示课程 prevCoursej 必须在课程 nextCoursej 之前 完成（先修课的关系）。同时给你一个下标从 0 开始的整数数组 time ，其中 time[i] 表示完成第 (i+1) 门课程需要花费的 月份 数。

请你根据以下规则算出完成所有课程所需要的 最少 月份数：

• 如果一门课的所有先修课都已经完成，你可以在 任意 时间开始这门课程。
• 你可以 同时 上 任意门课程 。

请你返回完成所有课程所需要的 最少 月份数。

注意： 测试数据保证一定可以完成所有课程（也就是先修课的关系构成一个有向无环图）。

示例 1:

输入：n = 3, relations = [[1,3],[2,3]], time = [3,2,5]
输出：8
解释：上图展示了输入数据所表示的先修关系图，以及完成每门课程需要花费的时间。
你可以在月份 0 同时开始课程 1 和 2 。
课程 1 花费 3 个月，课程 2 花费 2 个月。
所以，最早开始课程 3 的时间是月份 3 ，完成所有课程所需时间为 3 + 5 = 8 个月。

示例 2：

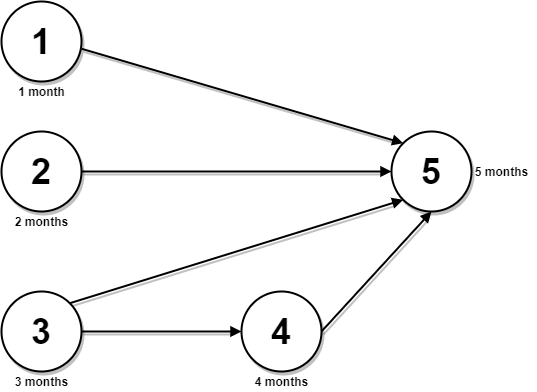
输入：n = 5, relations = [[1,5],[2,5],[3,5],[3,4],[4,5]], time = [1,2,3,4,5]
输出：12
解释：上图展示了输入数据所表示的先修关系图，以及完成每门课程需要花费的时间。
你可以在月份 0 同时开始课程 1 ，2 和 3 。
在月份 1，2 和 3 分别完成这三门课程。
课程 4 需在课程 3 之后开始，也就是 3 个月后。课程 4 在 3 + 4 = 7 月完成。
课程 5 需在课程 1，2，3 和 4 之后开始，也就是在 max(1,2,3,7) = 7 月开始。
所以完成所有课程所需的最少时间为 7 + 5 = 12 个月。

提示：

• 1 <= n <= 5 * 10^4
• 0 <= relations.length <= min(n * (n - 1) / 2, 5 * 10^4)
• relations[j].length == 2
• 1 <= prevCoursej, nextCoursej <= n
• prevCoursej != nextCoursej
• 所有的先修课程对 [prevCoursej, nextCoursej] 都是 互不相同 的。
• time.length == n
• 1 <= time[i] <= 10^4
• 先修课程图是一个有向无环图。

---

本题的实质是求 AOE 图上的最长路径。相似题目：

• 1857. 有向图中最大颜色值

解法1 记忆化搜索

要求出完成所有课程的最少月份数，可以求出每门课程的最少月份数，然后求出最大值。首先根据 $relations$，构建先修课邻接表表 $prev$，$prev[i]$ 就表示课程 $i$ 的所有的先修课。定义函数 $dp$ ，输入参数为 $i$ ，返回完成课程 $i$ 所需的最少月份数。

• 如果一门课程 $i$ 没有先修课要求，那么完成它的最少月份数就是 $time[i-1]$ 。
• 如果一门课有先修课时，完成它的最少月份数就是在它的所有先修课的最少完成月份的最大值的基础上，再加上 $time[i-1]$，即 $\text{dp}[i]=\text{max}(dp[j])+\text{time}[i-1],j\in \text{prev}[i]$ 。

可以运用记忆化搜索的技巧，求出每门课的最少完成月份数。因为运用了记忆化搜索，每门课的最少完成月份数最多只会被计算一次。

class Solution {
public:int minimumTime(int n, vector<vector<int>>& relations, vector<int>& time) {int mx = 0;vector<vector<int>> prev(n + 1);for (auto &r : relations) {int x = r[0], y = r[1];prev[y].emplace_back(x);}unordered_map<int, int> rec;function<int(int)> dp = [&](int i) -> int {if (!rec.count(i)) {int cur = 0;for (int p : prev[i]) cur = max(cur, dp(p));cur += time[i - 1];rec[i] = cur;}return rec[i];};for (int i = 1; i <= n; ++i) mx = max(mx, dp(i));return mx;}
};

复杂度分析：

• 时间复杂度：$O(m+n)$，其中 $O(m)$ 是数组 $relations$ 长度。需要构建先修课邻接表表，并且计算每个课程的最少月份数。因为每个课程只会被计算一次，因此相当于是每个 $relation$ 会被遍历一次。
• 空间复杂度：$O(m+n)$，先修课邻接表表的空间复杂度是 $O(m+n)$，记忆化搜索的空间复杂度是 $O(n)$ 。

---

解法2 动态规划

定义 $dp[i]$ 表示完成第 $i$ 门课程需要花费的最少月份数。根据题意，只有当 $i$ 的所有先修课程都完成时，才可以开始学习第 $i$ 门课程，并且可以立即开始。

因此，其中 $j$ 是 $i$ 的先修课程$$f[i]=\text{time}[i]+\underset{j}{\max }f[j]$$
由于题目保证图是一个有向无环图，所以一定存在拓扑序。我们可以在计算拓扑序的同时，计算状态转移。

具体来说，设当前节点为 $u$ ，我们可以在计算出 $dp[u]$ 后，更新 $v$ 的所有先修课程耗时的最大值，这里 $u$ 是 $v$ 的先修课程。答案就是所有 $dp[i]$ 的最大值。

class Solution {
private:vector<vector<int>> g;
public:int minimumTime(int n, vector<vector<int>>& relations, vector<int>& time) {g.resize(n);vector<int> ind(n);for (vector<int>& r : relations) {int x = r[0] - 1, y = r[1] - 1;g[x].push_back(y); // 建图++ind[y];}// 拓扑排序 queue<int> q;for (int i = 0; i < n; ++i)if (ind[i] == 0) // 没有先修课q.push(i); vector<int> dp(n);int ans = 0;while (!q.empty()) {int u = q.front(); q.pop(); // u出队意味着u的所有先修课都上完了// 出队的顺序就是拓扑序dp[u] += time[u]; // 加上当前课程的时间就得到了最终的dp[u]ans = max(ans, dp[u]);for (int v : g[u]) {dp[v] = max(dp[u], dp[v]); // 更新dp[v]的所有先修课程耗时的最大值if (--ind[v] == 0) { // v的先修课已上完q.push(v); }}}return ans;}  
};

复杂度分析：

• 时间复杂度：$O(m+n)$ ，其中 $O(m)$ 为 $relations$ 的长度。
• 空间复杂度：$O(m+m)$ 。