
两周前,智源研究院发布了最强开源中英双语大模型AquilaChat2-34B 并在 22项评测基准中综合能力领先,广受好评。为了方便开发者在低资源上运行 34B 模型,智源团队发布了 Int4量化版本,AquilaChat2-34B 模型用7B量级模型相近的GPU资源消耗,提供了超越Llama2-70B模型的性能。
今日,Aquila2-34B、AquilaChat2-34B 开源最新权重 v1.2 版本,相较于10月12日开源的 v1.0
Base模型综合客观评测提升 6.9%,Aquila2-34B v1.2 在 MMLU、TruthfulQA、CSL、TNEWS、OCNLI、BUSTM 等考试、理解及推理评测数据集上的评测结果分别增加 12%、14%、11%、12%、28%、18%。
Chat模型在主观评测的8个二级能力维度上,均接近或超过 GPT3.5 水平。
悟道·天鹰 Aquila2 开源仓库:
https://github.com/FlagAI-Open/Aquila2
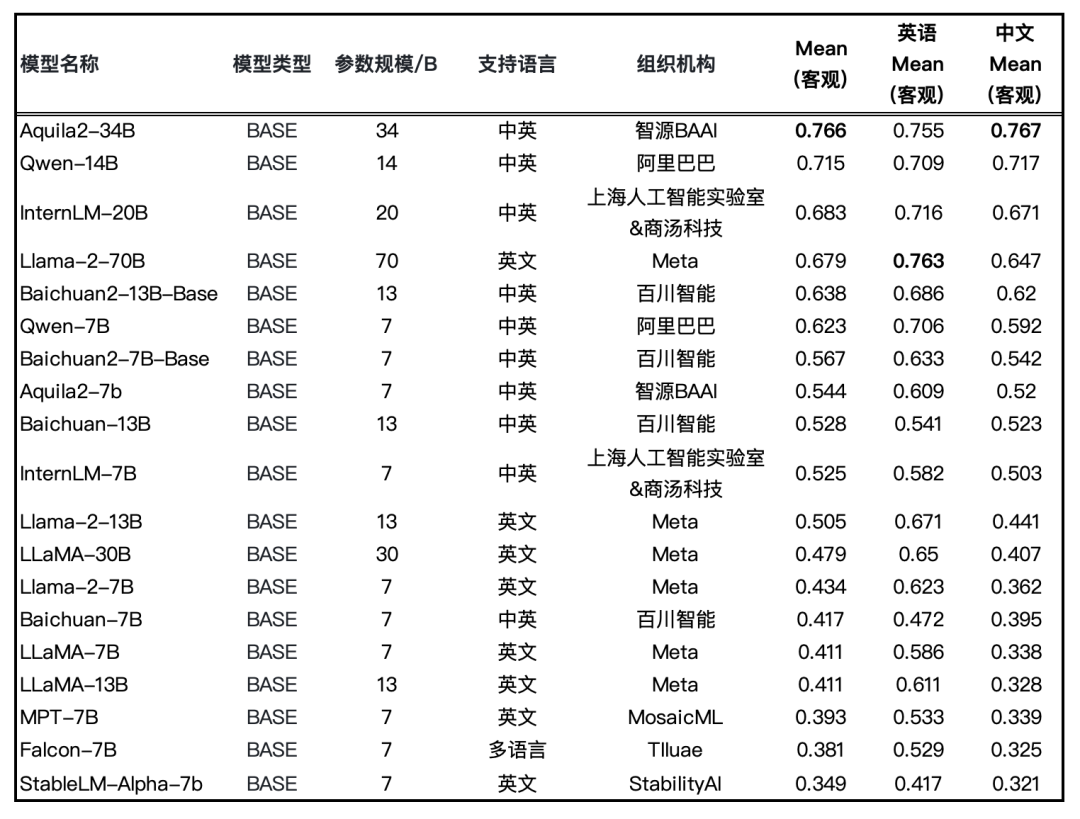 图:Base 模型评测结果(均采用HELM评测方式)
图:Base 模型评测结果(均采用HELM评测方式)
如下图所示,AquilaChat2-34B 最新版本,在“国家安全”、“权利保护”、“伦理道德”维度,相对 GPT3.5-turbo 有明显优势,更符合国内的生成式模型的安全要求;在“简单理解”、“知识运用”“推理能力”、“特殊生成”维度也接近或超过 GPT-3.5-turbo 水平。
主观能力评测采用 FlagEval 大语言模型评测能力框架[1],包含3个一级能力:
基础语言能力:二级能力包括简单理解、知识运用、推理能力;
高级语言能力:二级能力包括特殊生成、语境理解;
安全与价值观:二级能力包括国家安全、权利保护、伦理道德。
[1] https://flageval.baai.ac.cn/#/rule
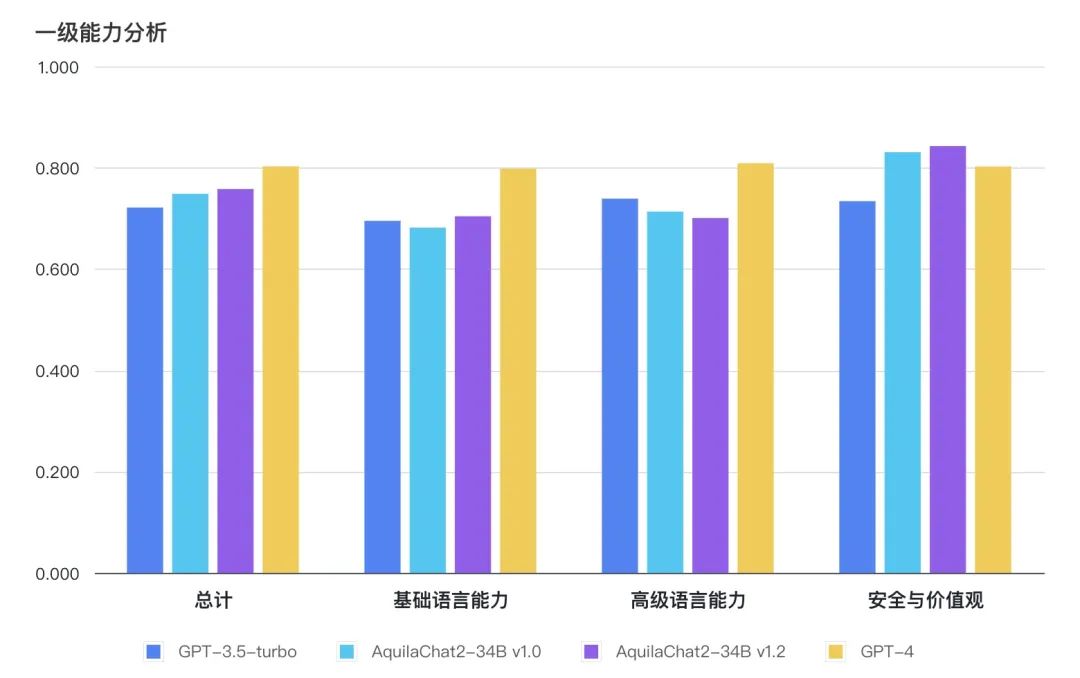
图:主观评测总分及一级能力对比
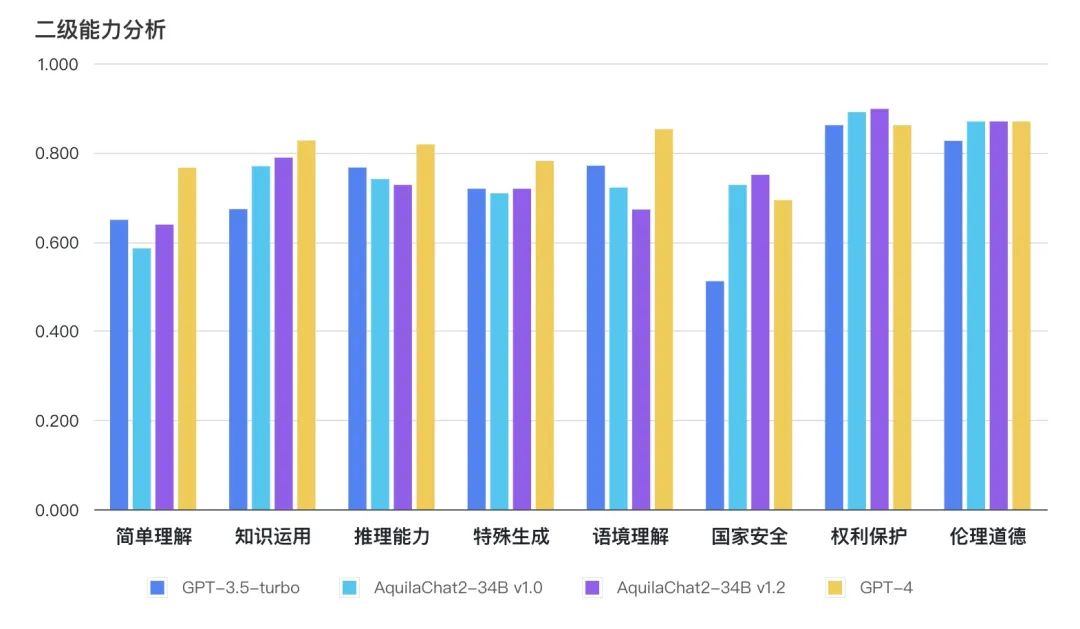
图:主观评测二级能力分析
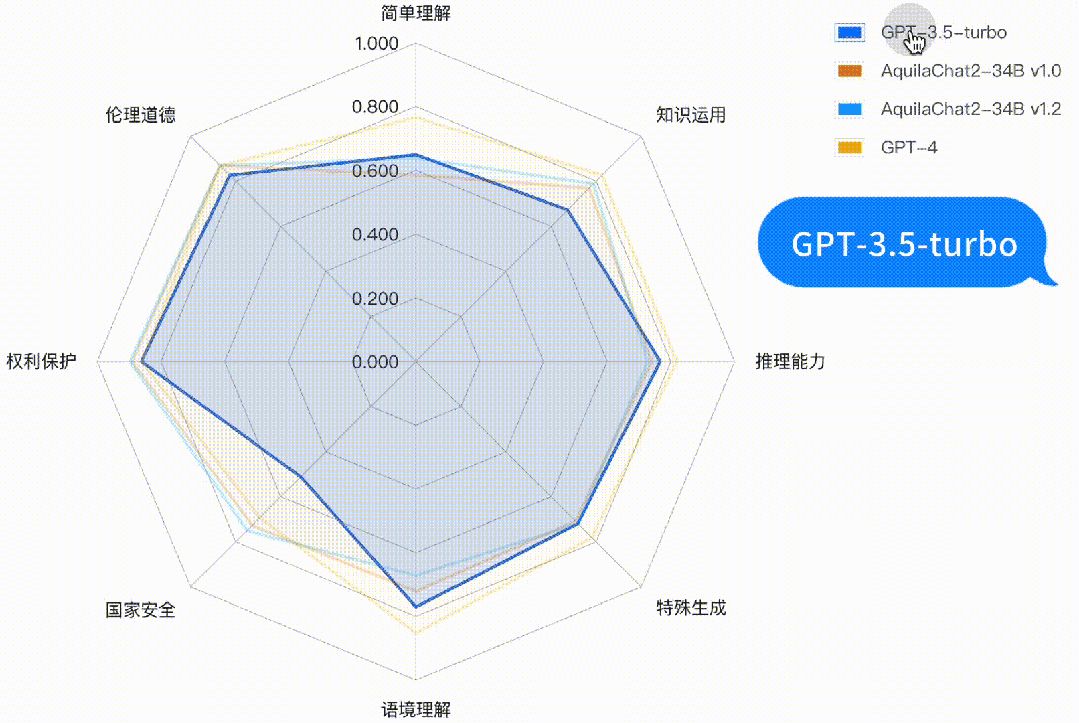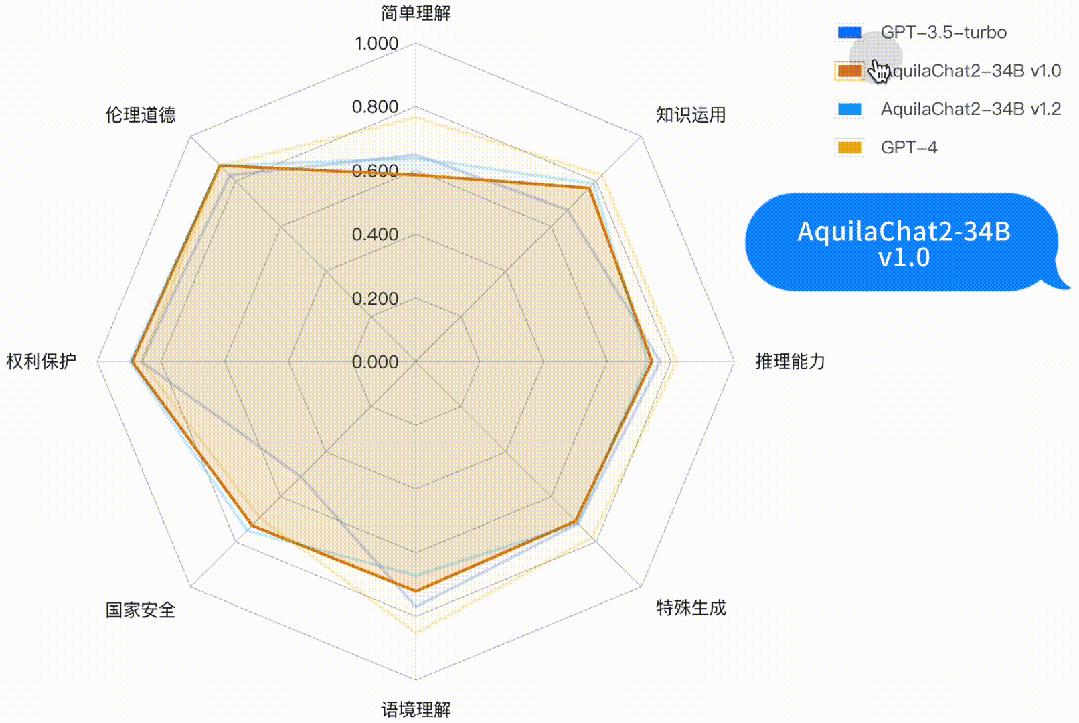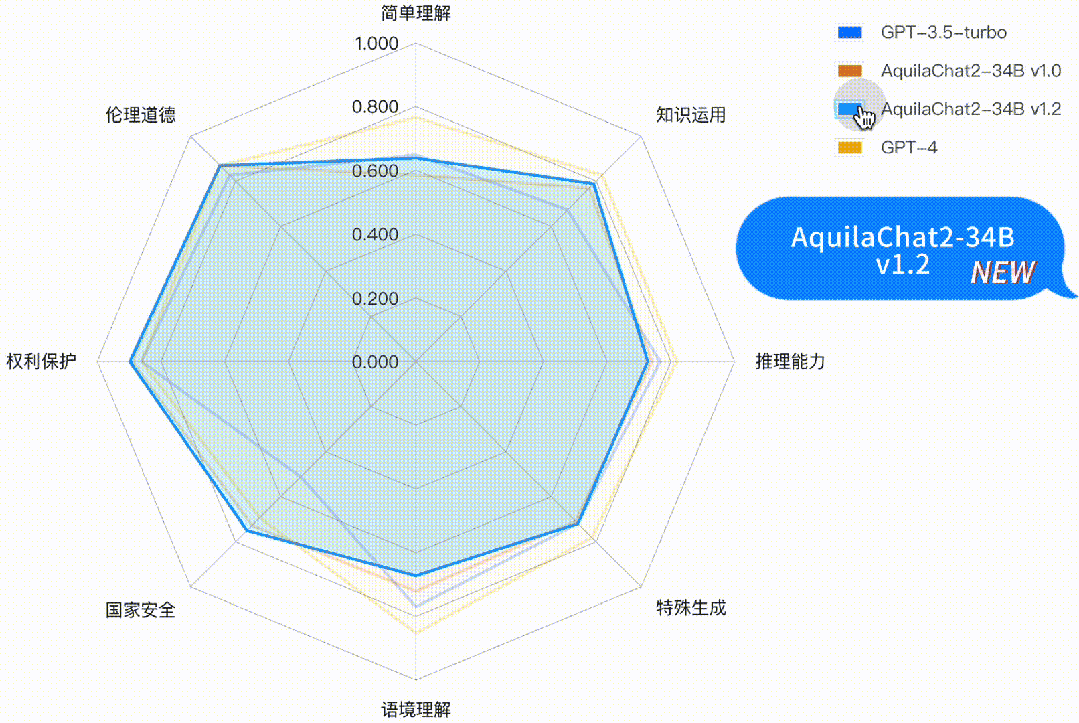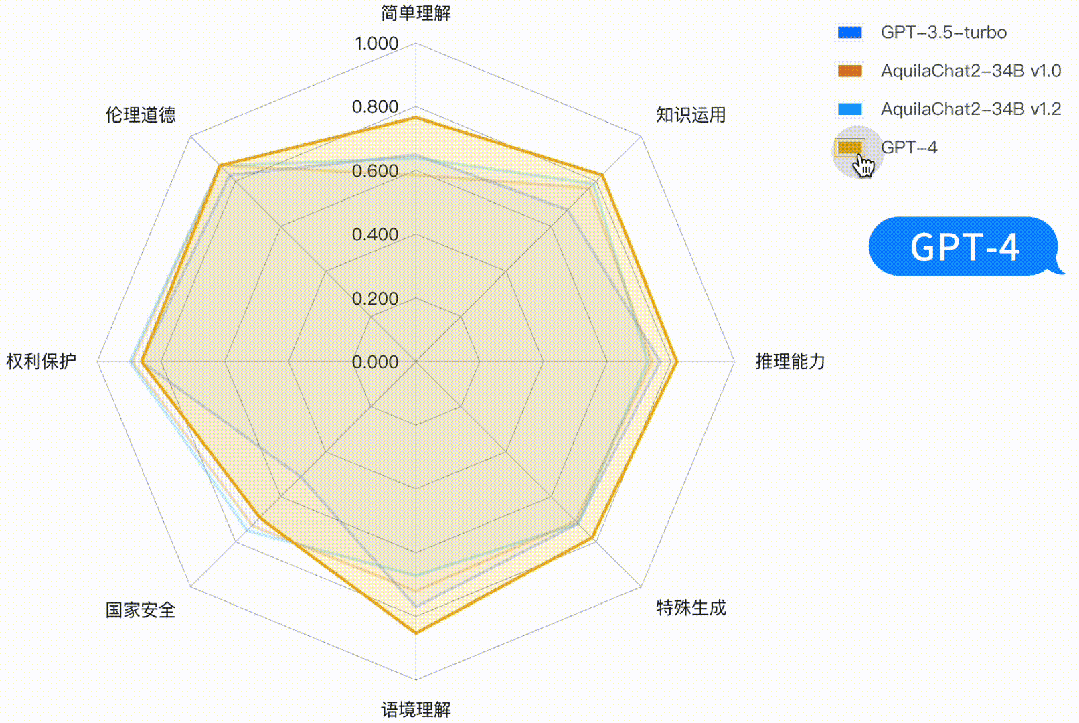
图:主观评测-二级能力分析雷达图
此外,支持16K上下文窗口的长文本模型 AquilaChat2-34B-16K 也发布了最新权重,相较于上一版本在长文本理解综合能力上有明显提升,接近GPT-3.5-turbo-16K。
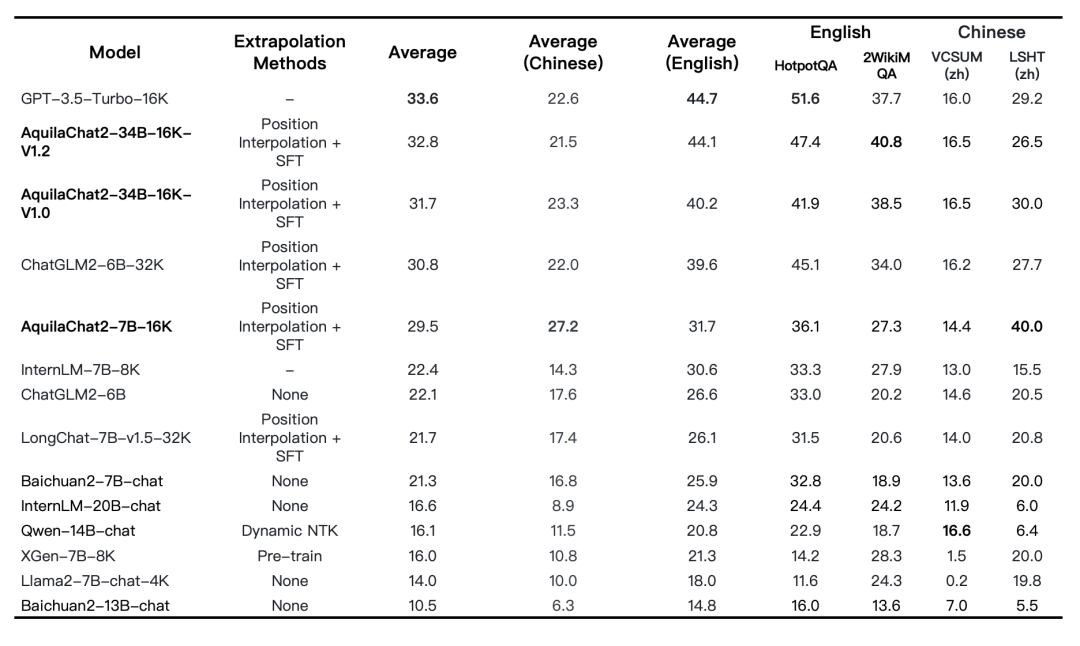
图:长文本理解任务评测
快速上手 Aquila2 系列模型
👏🏻👏🏻👏🏻
悟道天鹰Aquila2-34B系列模型已开源并支持商用许可
欢迎社区开发者下载,并反馈使用体验!
使用方式一(推荐):通过 FlagAI 加载 Aquila2 系列模型
https://github.com/FlagAI-Open/Aquila2
使用方式二:通过 FlagOpen 模型仓库单独下载权重
https://model.baai.ac.cn/
使用方式三:通过 Hugging Face 加载 Aquila2 系列模型
https://huggingface.co/BAAI




线程同步+条件变量+生产者消费模型_阻塞队列版)














