一、计算机网络
1.1、考情分析

2.1 TCP/IP协议簇
2.1.1常见协议及功能

网际层是整个TCP/IP体系结构的关键部分,其功能是使主机可以把分组发往任何网络并使分组独立地传向目标。
- POP3: 110 端口,邮件收取
- SMTP: 25 端口,邮件发送
- FTP: 20数据端口/21控制端口,文件传输协议
- HTTP: 80端口,超文本传输协议,网页传输
- DHCP: 67 端口,IP地址自动分配
- SNMP: 161 端口,简单网络管理协议
- DNS: 53端口,域名解析协议,记录域名与IP的映射关系
- TCP:可靠的传输层协议,TCP协议可以依据端口号将报文交付给上层的某一进程, 可以对应用层进程进行寻址。
- UDP:不可靠的传输层协议
- ICMP:因特网控制协议,PING命令来自该协议
- IGMP:组播协议
- ARP:地址解析协议,IP地址转换为MAC地址
- RARP:反向地址解析协议,MAC地址转IP地址
2.1.2 DHCP
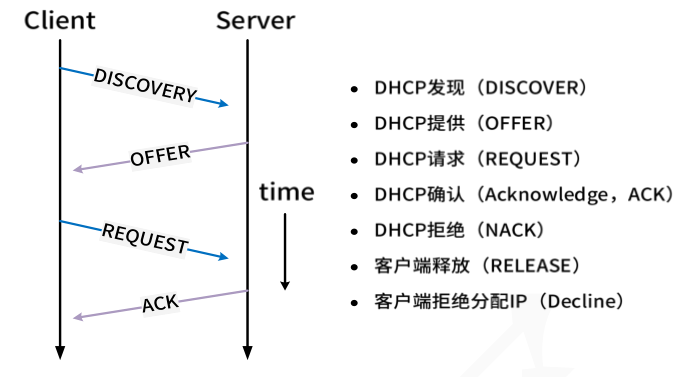
动态主机配置协议(DHCP, Dynamic Host Configuration Protocol)
(1)客户机/服务器模型
(2)租约默认为8天
(3)当租约过半时,客户机需要向DHCP服务器申请续租;
(4)当租约超过87.5%时,如果仍然没有和当初提供IP的DHCP服务器联系上,则开始联系其他的DHCP服务器。
(5)固定分配、动态分配和自动分配。
(6)分配失败则IP显示为169.254.X.X (Windows)和0.0.0.0 (Linux)
2.1.3 DNS用法
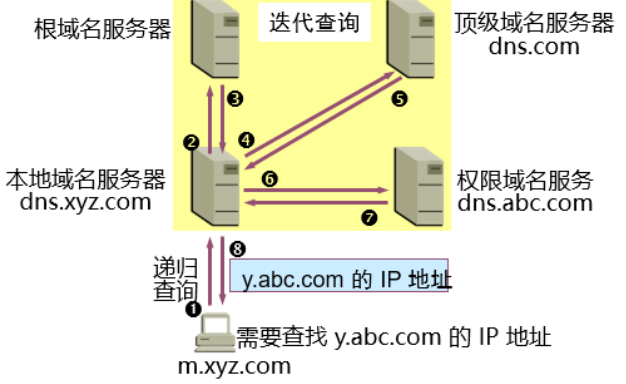
(1) 查询方式
递归查询:服务器必须回答目标IP与域名的映射关系。
迭代查询:服务器收到一次迭代查询回复-次结果,这个结果不一-定是目标IP与域名的映射关系,也可以是其它DNS服务器的地址。
(2)查询过程
本机查询一般先查找本机HOST文件,没有相关映射时,查询域名服务器;
主机向本地域名服务器的查询一般采用的都是递归查询;
如果主机所询问的本地域名服务器不知道被查询域名的IP地址,那么本地域名服务器就以DNS客户的身份,向其他根域名服务器继续发出查询请求报文;
本地域名服务器向根域名服务器的查询通常是采用迭代查询。当根域名服务器收到本地域名服务器的迭代查询请求报文时,要么给出所要查询的IP地址,要么告诉本地域名服务器:“你下一 步应当向哪一个域名服务器进行查询”。然后让本地域名服务器进行后续的查询。
根服务器或者流量较大的域名服务器都不使用递归查询,其原因也很简单,大量的递归查询会导致服务器过载;
在Linux系统中,DNS配置文件resolv.conf的关键字主要有四个,分别是:
- nameserver :定义DNS服务器的IP地址
- domain :定义本地域名
- search :定义域名的搜索列表
- sortlist :对返回的域名进行排序
二、 数学与经济管理
2.1、考情分析
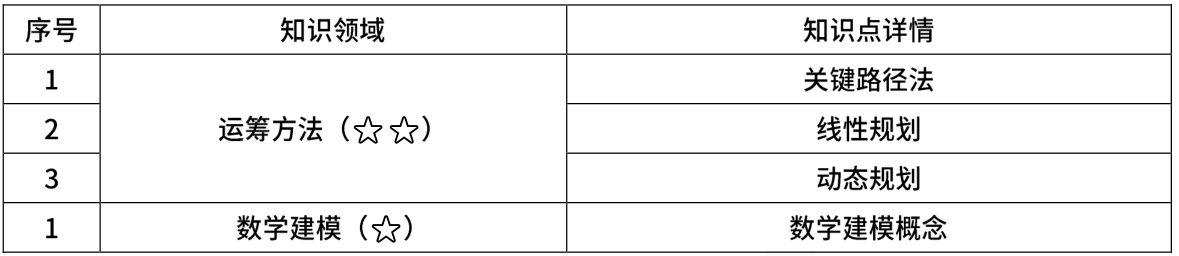
2.2 考点精讲
2.2.1运筹方法
线性规划(线性规划问题的数学模型通常由线性目标函数、线性约束条件、变量非负条件组成) ,
特点如下:
- (1)线性规划的可行解域是由一组线性约束条件形成的,从几何意义来说,就是由一-些线性解面围割形成的区域,不-定是封闭的多边形或多面体。
- (2)如果存在两个最优解,则连接这两点的线段内所有的点都是最优解,而线段两端延长线上可能会超出可行解区。
- (3)增加一个约束条件时,要么缩小可行解域(新的约束条件分割了原来的可行解域),要么可行解域不变(新的约束条件与原来的可行解域不相交)
- (4)如果最优解在可行解域边界某个非顶点处达到,则随着等值域向某个方向移动,目标函数的值会增加或减少(与 最优解矛盾)或没有变化(在此段边界.上都达到最优解) ,从而仍会在可行解域的某个顶点处达到最优解。若最优解存在且唯一-,则可以从可行解区顶点处比较目标函数值来求解。
动态规划
关键路径法
2.2.2数学建模
2.2.2.1概念
数学建模是一种数学的思考方法,是运用数学的语言和方法,通过抽象和简化,建立能近似刻画并解决实际问题的模型的一种强有力的数学手段。
2.2.2.2建模过程
(1)模型准备:了解问题的实际背景,明确其实际意义,掌握对象的各种信息。用数学语言来描述问题。
(2)模型假设:根据实际对象的特征和建模的目的,对问题进行必要的简化,并用精确的语言提出一些恰当的假设。
(3)模型建立:在假设的基础,上,利用适当的数学工具来刻画各变量之间的数学关系,建立相应的数学结构。只要能够把问题描述清楚,尽量使用简单的数学工具。
(4)模型求解:利用获取的数据资料,对模型的所有参数做出计算(估计)。
(5)模型分析:对所得的结果进行数学上的分析。
(6)模型检验:将模型分析结果与实际情形进行比较,以此来验证模型的准确性、合理性和适用性。如果模型与实际较吻合,则要对计算结果给出其实际含义,并进行解释。如果模型与实际吻合较差,则应该修改假设,再次重复建模过程。
(7)模型应用:应用方式因问题的性质和建模的目的而异。
2.2.2.3数学建模方法和思路
- (1)直接分析法:认识原理,直接构造出模型。
- (2)类比法:根据类似问题模型构造新模型。
- (3)数据分析法:大量数据统计分析之后建模。
- (4)构想法:对将来可能发生的情况给出设想从而建模。
2.2.2.4模型分析
(1)模型的合理性分析:最佳、适中、满意等。
利用实际案例数据对模型进行检验。
可以请专家来分析模型是否合理。
利用计算机来模拟实际问题,再在计算机.上检验该数学模型。
(2)模型的误差分析:模型误差、观测误差、截断误差、舍入误差、过失误差、绝对误差、相对误差等。
(3)参数的灵敏性分析:变量数据是否敏感,在最优方案不变的条件下这些变量允许变化的范围。
三、知识产权与标准化
3.1、考情分析

3.2、考点精讲
3.2.1、知识产权
3.2.1.1、保护对象
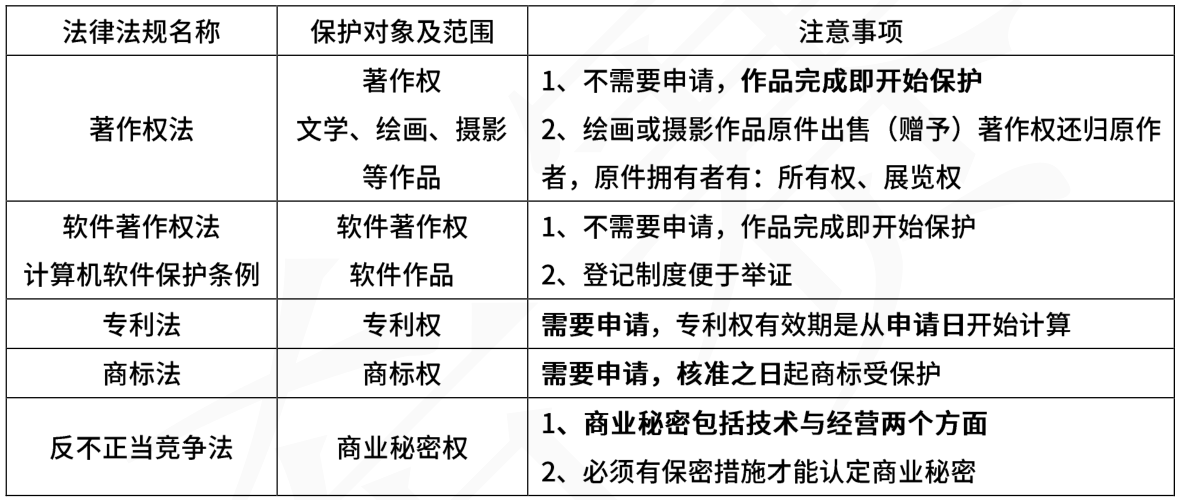
3.2.1.2、保护期限
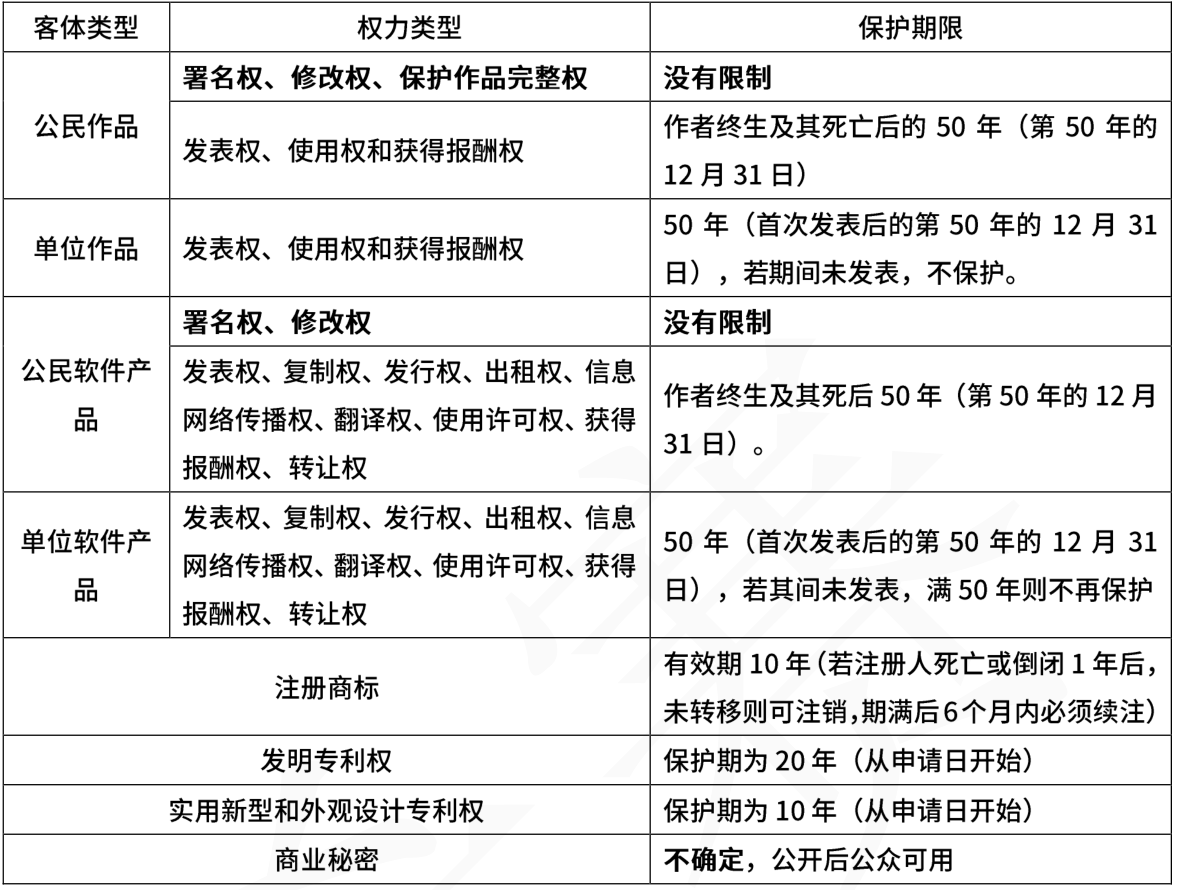
3.2.1.3、知识产权人确定
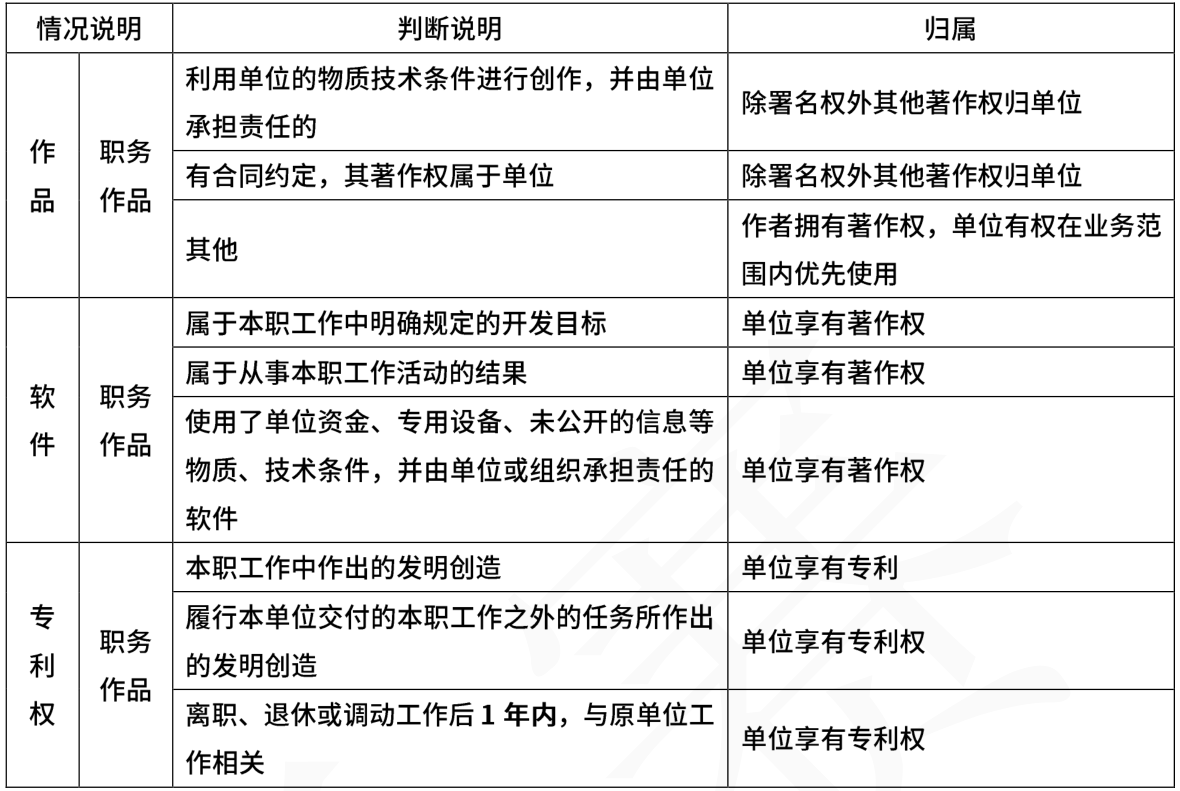
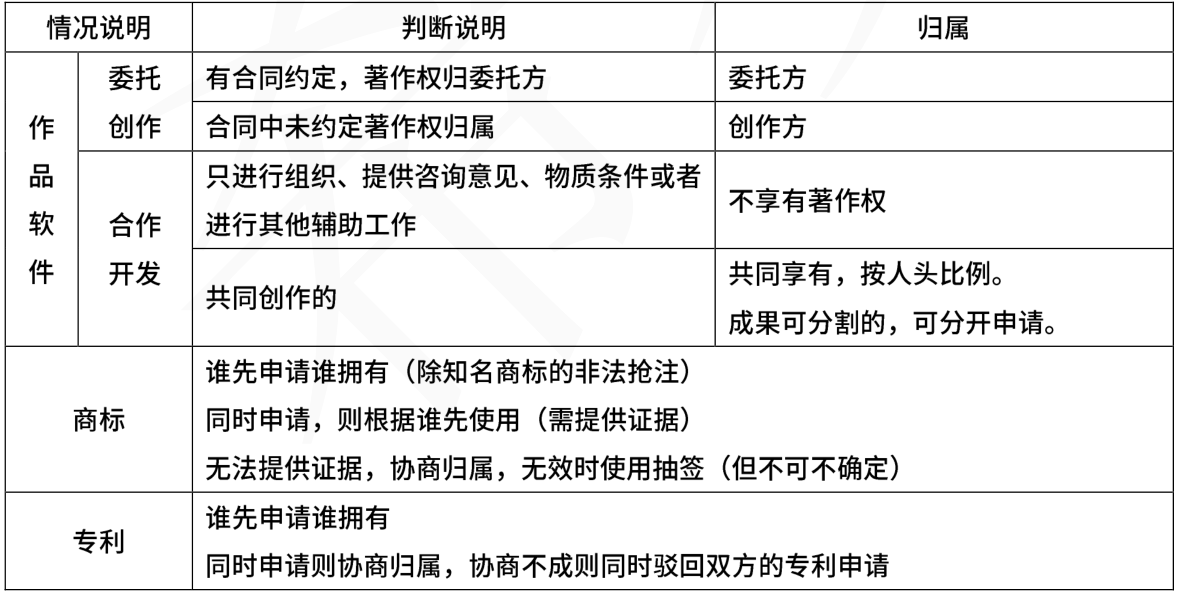
3.2.1.4、侵权判断
(1)适用情景
中国公民、法人或者其他组织的作品,不论是否发表,都享有著作权。
开发软件所用的思想、处理过程、操作方法或者数学概念不受保护。
著作权法不适用于下列情形:
法律、法规,国家机关的决议、决定、命令和其他具有立法、行政、司法性质的文件,及其官方正式译文;
时事新闻;
历法、通用数表、通用表格和公式。
(2)常见侵权与合理引用区分
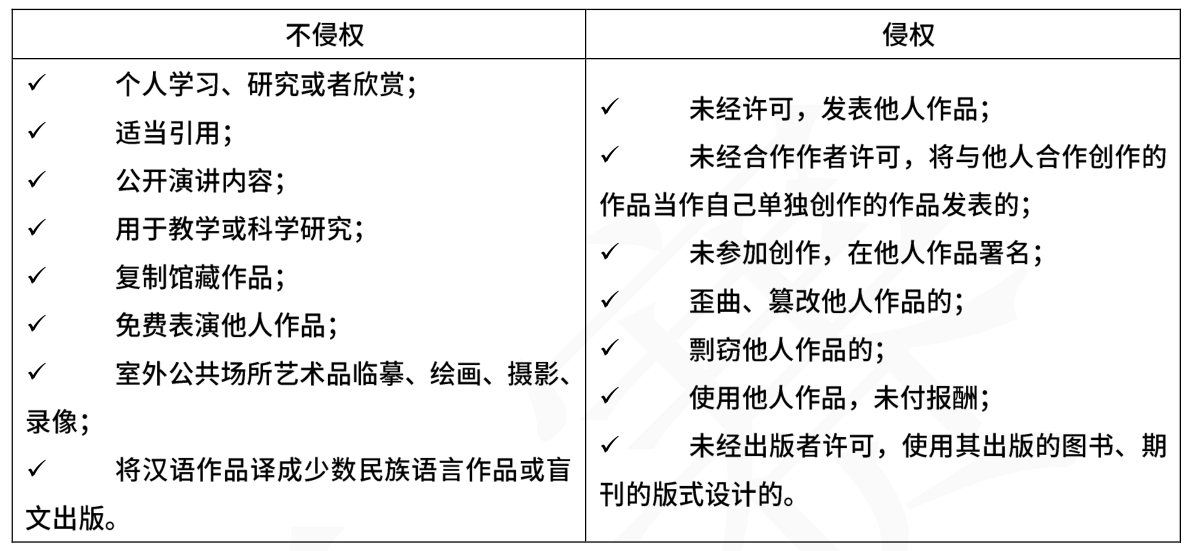

)





出现的问题)


)
)







