Composite 组合模式和后面谈到的Iterator,Chain of Resposibility都属于“数据结构”模式。Composite 组合模式核心是通过多态的递归调用解耦内部和外部的依赖关系。
文章目录
- 1. “数据结构”模式
- 1.1 典型模式
- 2. 动机( Motivation )
- 3. 模式定义
- 4. Composite 组合模式代码分析
- 5. 结构(Structure)
- 6. 要点总结
- 7. 其他参考
1. “数据结构”模式
常常有一些组件在内部具有特定的数据结构,如果让客户程序依赖这些特定的数据结构,将极大地破坏组件的复用。这时候,将这些特定数据结构封装在内部,在外部提供统一的接口,来实现与特定数据结构无关的访问,是一种行之有效的解决方案
1.1 典型模式
-
Composite
-
Iterator
-
Chain of Resposibility
2. 动机( Motivation )
-
软件在某些情况下,客户代码过多地依赖于对象容器复杂的内部实现结构,对象容器内部实现结构(而非抽象接口)的变化将起客户代码的频繁变化,带来了代码的维护性、扩展性等弊端。
-
如何将“客户代码与复杂的对象容器结构”解耦?让对象容器自己来实现自身的复杂结构,从而使得客户代码就像处理简单对象一样来处理复杂的对象容器 ?
3. 模式定义
- 将对象组合成
树形结构以表示“部分-整体”的层次结构。Composite使得用户对单个对象和组合对象的使用具有一致性(稳定)。
----《设计模式》GoF
这里的一致性指下面的代码在使用时,不论是树节点还是叶子结点,使用方法都是一致的。
process(root);process(leaf2);process(treeNode3);
4. Composite 组合模式代码分析
典型树结构的数据处理,访问的时候使用多态的方式将树形结构的访问封装到了树形结构的内部,而不是要把树形结构暴露在外部。
#include <iostream>
#include <list>
#include <string>
#include <algorithm>using namespace std;class Component
{
public:virtual void process() = 0;virtual ~Component(){}
};//树节点
class Composite : public Component{string name;list<Component*> elements;
public:Composite(const string & s) : name(s) {}void add(Component* element) {elements.push_back(element);}void remove(Component* element){elements.remove(element);}void process(){//1. process current node//2. process leaf nodesfor (auto &e : elements)e->process(); //多态调用}
};//叶子节点
class Leaf : public Component{string name;
public:Leaf(string s) : name(s) {}void process(){//process current node}
};void Invoke(Component & c){//...c.process();//...
}int main()
{Composite root("root");Composite treeNode1("treeNode1");Composite treeNode2("treeNode2");Composite treeNode3("treeNode3");Composite treeNode4("treeNode4");Leaf leat1("left1");Leaf leat2("left2");root.add(&treeNode1);treeNode1.add(&treeNode2);treeNode2.add(&leaf1);root.add(&treeNode3);treeNode3.add(&treeNode4);treeNode4.add(&leaf2);process(root);process(leaf2);process(treeNode3);}
代码分析:
首先定义一个抽象接口
class Component
{
public:virtual void process() = 0;virtual ~Component(){}
};
定义了一个树形结构
//树节点
class Composite : public Component{string name;list<Component*> elements;
public:Composite(const string & s) : name(s) {}void add(Component* element) {elements.push_back(element);}void remove(Component* element){elements.remove(element);}void process(){//1. process current node//2. process leaf nodesfor (auto &e : elements)e->process(); //多态调用}
};
list<Component*> elements;构成子节点,子节点类型为Component,树节点和下面的叶子结点都可以加入树节点类型,也就是list中的对象可能是Composite,也可能是Leaf,因此list<Component*> elements;也就表达了树形结构。
add()和remove()是树形结构的操作。
process()方法是对父类的override,有两个步骤的处理,第一个步骤是处理当前节点,第二步是处理叶子结点,叶子结点是用循环,e->process()是虚函数的调用,如果当前是Composite证明调用的是自身,如果是Leaf,就会调用到Leaf的process(),也就不会再循环。这里是一种递归的思想。
这样就完成Component树节点下的所有树节点。
另外定义叶子结点
//叶子节点
class Leaf : public Component{string name;
public:Leaf(string s) : name(s) {}void process(){//process current node}
};
也继承自 Component。
假如有一个客户的处理程序:接受Component作为参数,进去后调用c.process();实现多态调用
void Invoke(Component & c){//...c.process();//...
}
以下示意性的演示使用
int main()
{Composite root("root");Composite treeNode1("treeNode1");Composite treeNode2("treeNode2");Composite treeNode3("treeNode3");Composite treeNode4("treeNode4");Leaf leat1("left1");Leaf leat2("left2");root.add(&treeNode1);treeNode1.add(&treeNode2);treeNode2.add(&leaf1);root.add(&treeNode3);treeNode3.add(&treeNode4);treeNode4.add(&leaf2);process(root); //处理根节点process(leaf2); //处理叶节点process(treeNode3); //处理treeNode3}
假如不使用Composite 组合模式,也就是不使用以下代码
for (auto &e : elements)e->process(); //多态调用
在以下代码中的process()就需要分别处理:当类型是composite或者leaf怎么处理
void Invoke(Component & c){//...c.process();//...
}
实际上以下代码是将内部数据结构访问封装
for (auto &e : elements)e->process(); //多态调用
访问的时候使用多态的方式将树形结构的访问封装到了树形结构的内部,而不是要把树形结构暴露在外部。
5. 结构(Structure)
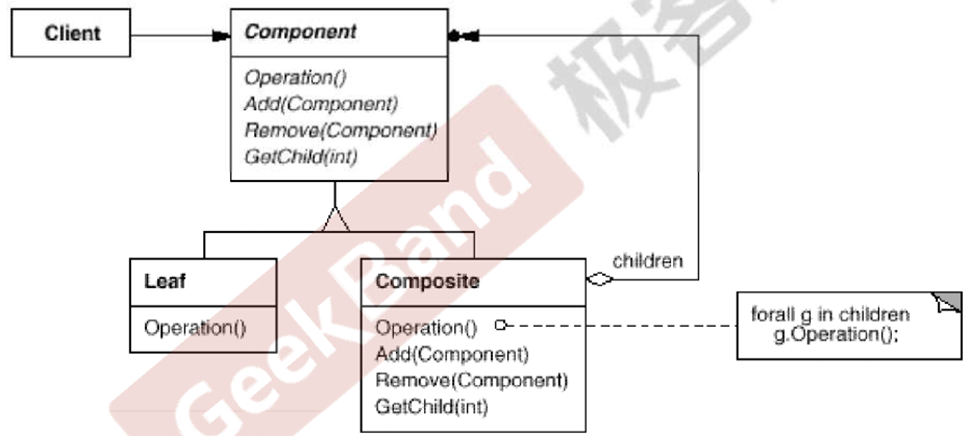
Add()、Remove()、GetChild()其实是由争议的,是放在父类Component还是Composite子类中都有不完善的地方,如果放在父类里,对于Leaf结点就比较尴尬,Leaf结点是子节点了,还可以Add()、Remove()、GetChild()吗?显然不行,不写实现内容也不舒服。所以有的实现也是我们此处实现的,就是压根不提供Add()、Remove()、GetChild()这些。换句话说在父类Component中不提供,但是在Composite子类中提供。怎么解决都有不完美的地方,但是此处的实现还是比较好些。
重点是在forall g in children;g.Operation():,Operation()中处理当前节点,接着使用多态递归调用的方式处理所有子节点
上图是比较粗略的表达了Composite 组合模式,这里的核心是用多态调用方式针对树形结构和叶子结点。
6. 要点总结
- Composite模式采用树形结构来实现普遍存在的对象容器,从而将“一对多”的关系转化为“一对一”的关系,使得客户代码可以一致地(复用)处理对象和对象容器,无需关心处理的是单个的对象,还是组合的对象容器。
如果不使用那个核心代码for (auto &e : elements) e->process(); //多态调用,就需要在c.process();中去一会实现一对一(Leaf),一会实现一对多(Composite)的关系。
- 将“客户代码与复杂的对象容器结构”解耦是Composite的核心思想,解耦之后,客户代码将与纯粹的抽象接口一一而非对象容器的内部实现结构一一发生依赖,从而更能“应对变化“。
外部无需关心内部的是树还是叶子,只统一的处理;“客户代码将与纯粹的抽象接口发生依赖”:Invoke(Component & c)中接受的参数是Component抽象类
- Composite模式在具体实现中,可以让父对象中的子对象反向追溯;如果父对象有频繁的遍历需求,可使用缓存技巧来改善效率。
7. 其他参考
C++设计模式——组合模式

![【esp32]VSCode-SPI控制OLED](http://pic.xiahunao.cn/【esp32]VSCode-SPI控制OLED)










/自定义label))



![[Shell] ${} 的多种用法](http://pic.xiahunao.cn/[Shell] ${} 的多种用法)
——主时钟约束)

