业务需求
将用户敏感信息脱敏展示到前端是出于保护用户隐私和信息安全的考虑。
敏感信息包括但不限于手机号码、身份证号、银行卡号等，这些信息泄露可能导致用户个人信息的滥用、身份盗用等严重问题。脱敏是一种常用的保护用户隐私的方式，它的目的是减少潜在的风险，同时保持一定的用户信息可读性。
比如咱们在选择用户信息以及展示选座信息时，用户证件号码的脱敏展示。
常用脱敏规则 ：替换、重排、加密、截断、掩码
Hutool 工具类实现数据脱敏
Hutool包含的组件
Hutool官方文档
https://www.hutool.cn/docs/#/core/%E5%B7%A5%E5%85%B7%E7%B1%BB/%E4%BF%A1%E6%81%AF%E8%84%B1%E6%95%8F%E5%B7%A5%E5%85%B7-DesensitizedUtil
<dependency> <groupId>cn.hutool</groupId> <artifactId>hutool-all</artifactId> <version>5.8.16</version>
</dependency>注意 ：Hutool 5.x支持JDK8+， 如果你的项目使用JDK7，请使用
Hutool 4.x版本。本文使用的数据脱敏工具类只有在5.6+版本以上才提供。Hutool作为一个Java基础工具类，对文件、流、加密解密、转码、正则、线程、XML等JDK方法进行封装，组成各种Util工具类，同时提供以下组件：
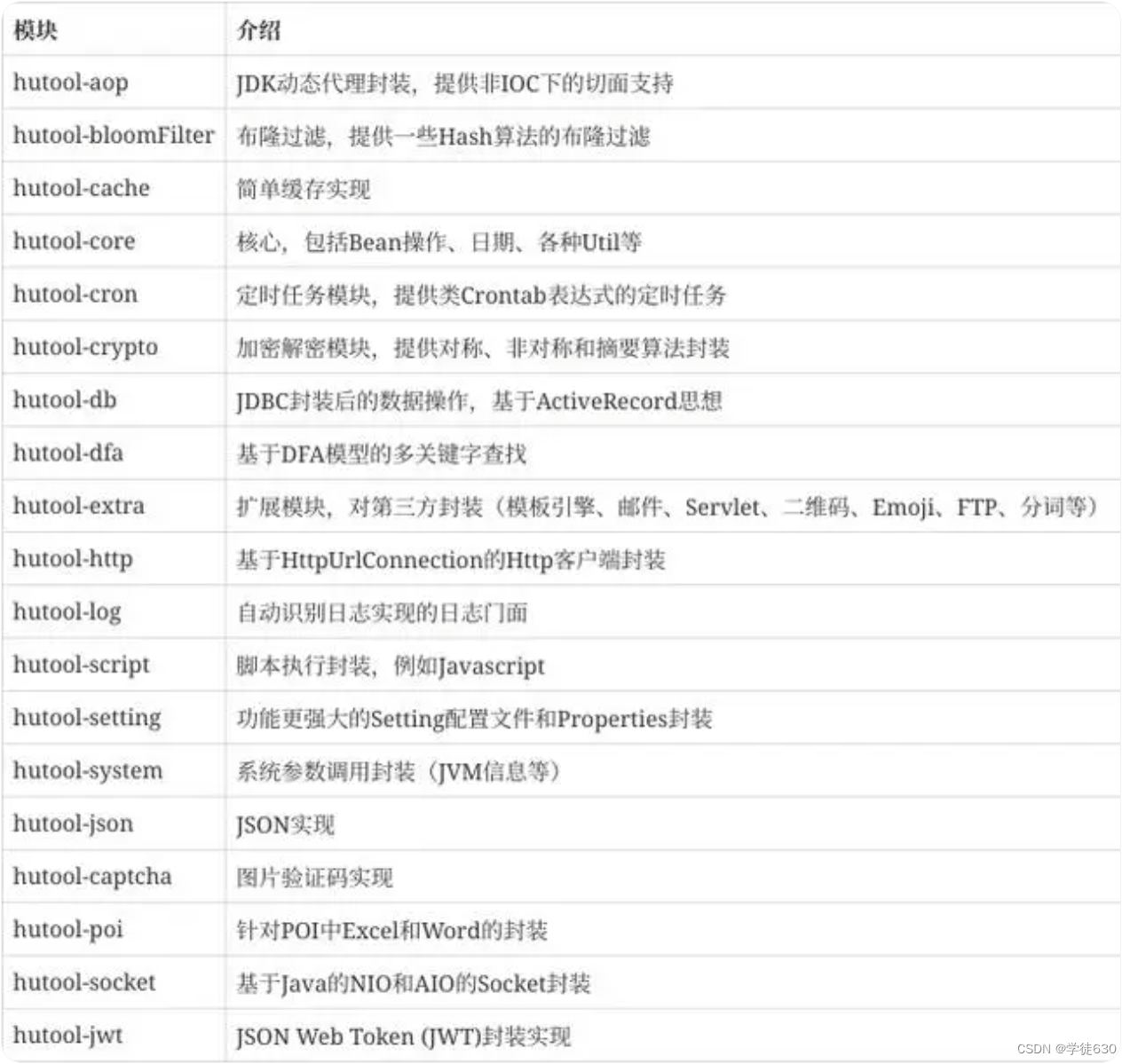
可以根据需求对每个模块单独引入，也可以通过引入hutool-all方式引入所有模块，本文所使用的数据脱敏工具就是在hutool.core模块。
Hutool支持的脱敏数据类型
Hutool针对数据脱敏业务为不同的敏感数据提供了相应的API来实现脱敏操作，现阶段最新版本的Hutool支持的脱敏数据类型如下，基本覆盖了常见的敏感信息。
- 用户id
- 中文姓名
- 身份证号
- 座机号
- 手机号
- 地址
- 电子邮件
- 密码
- 中国大陆车牌，包含普通车辆、新能源车辆
- 银行卡
Hutool提供的脱敏方法如下图所示：
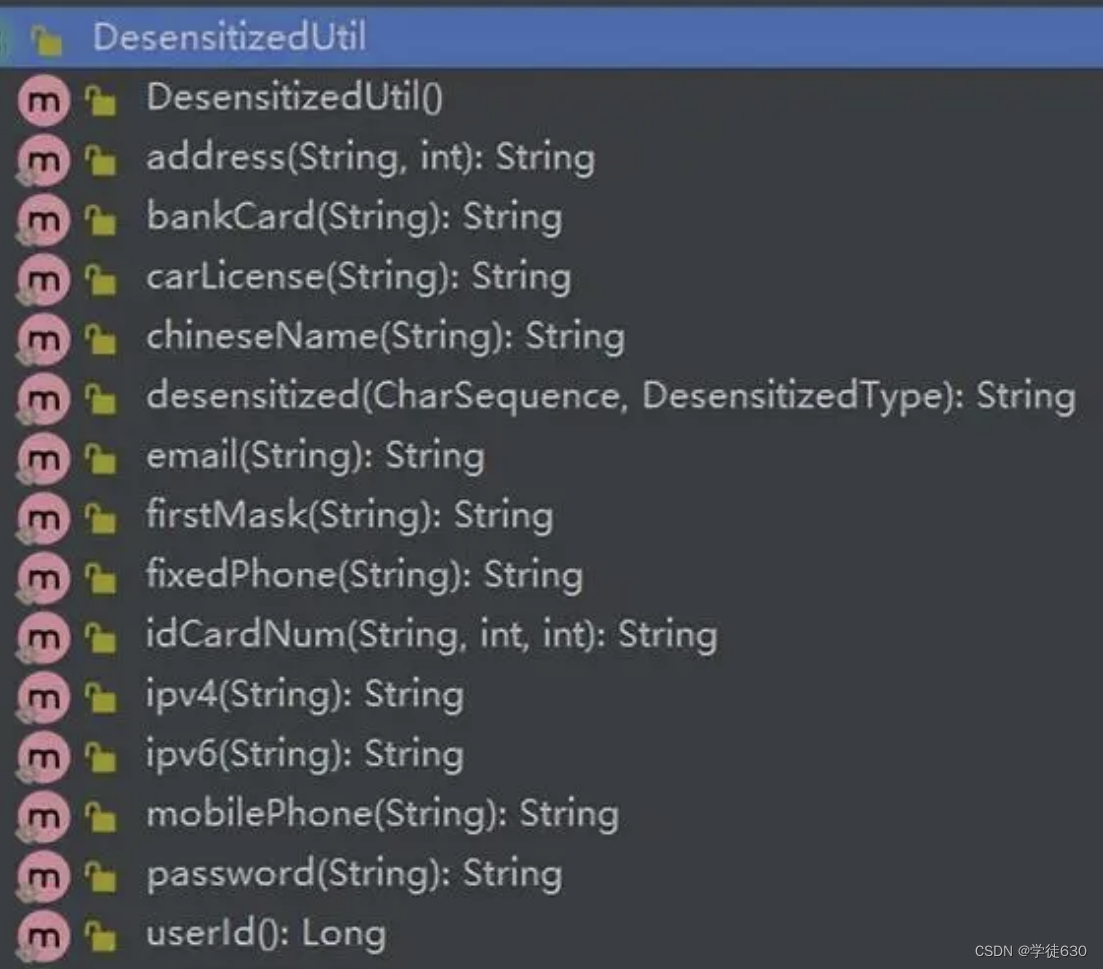
注意 ：Hutool 脱敏是通过 * 来代替敏感信息的，具体实现是在StrUtil.hide( )方法中，如果我们想要自定义隐藏符号，则可以把Hutool的源码拷出来，重新实现即可。
API演示：
/*** 【手机号码】前三位，后4位，其他隐藏，比如135****2210** @param num 移动电话；* @return 脱敏后的移动电话；*/public static String mobilePhone(String num) {if (StrUtil.isBlank(num)) {return StrUtil.EMPTY;}return StrUtil.hide(num, 3, num.length() - 4);}/*** 【地址】只显示到地区，不显示详细地址，比如：北京市海淀区****** @param address 家庭住址* @param sensitiveSize 敏感信息长度* @return 脱敏后的家庭地址*/public static String address(String address, int sensitiveSize) {if (StrUtil.isBlank(address)) {return StrUtil.EMPTY;}int length = address.length();return StrUtil.hide(address, length - sensitiveSize, length);}/*** 【密码】密码的全部字符都用*代替，比如：******** @param password 密码* @return 脱敏后的密码*/public static String password(String password) {if (StrUtil.isBlank(password)) {return StrUtil.EMPTY;}return StrUtil.repeat('*', password.length());}搭建Jackson序列化体系
现在有了数据脱敏工具类，如果前端需要显示数据数据的地方比较多，我们不可能在每个地方都调用一个工具类，这样就显得代码太冗余了，那我们如何通过注解的方式优雅的完成数据脱敏呢？
实现思路
在 SpringMVC 返回数据时，通过默认的 Jackson 序列化器进行指定，替换为咱们已经包装后的序列化器，这样就能依赖现有解决方案，降低技术复杂度。
代码实现
定义手机号和证件号的 Jackson 自定义序列化器，并在对应需要脱敏的敏感字段上指定自定义序列化器。
1）身份证号序列化器。
/*** 身份证号脱敏反序列化** @公众号：马丁玩编程，回复：加群，添加马哥微信（备注：12306）获取项目资料*/
public class IdCardDesensitizationSerializer extends JsonSerializer<String> {@Overridepublic void serialize(String idCard, JsonGenerator jsonGenerator, SerializerProvider serializerProvider) throws IOException {String phoneDesensitization = DesensitizedUtil.idCardNum(idCard, 4, 4);jsonGenerator.writeString(phoneDesensitization);}
}2）手机号序列化器。
/*** 手机号脱敏反序列化** @公众号：马丁玩编程，回复：加群，添加马哥微信（备注：12306）获取项目资料*/
public class PhoneDesensitizationSerializer extends JsonSerializer<String> {@Overridepublic void serialize(String phone, JsonGenerator jsonGenerator, SerializerProvider serializerProvider) throws IOException {String phoneDesensitization = DesensitizedUtil.mobilePhone(phone);jsonGenerator.writeString(phoneDesensitization);}
}3）敏感字段上自定义序列化器。
/*** 乘车人返回参数** @公众号：马丁玩编程，回复：加群，添加马哥微信（备注：12306）获取项目资料*/
@Data
@Accessors(chain = true)
public class PassengerRespDTO {/*** 证件号码*/@JsonSerialize(using = IdCardDesensitizationSerializer.class)private String idCard;/*** 手机号*/@JsonSerialize(using = PhoneDesensitizationSerializer.class)private String phone;
}完成上述步骤后，前端调用 HTTP 请求获取数据时，SpringMVC 通过 Jackson 进行序列化数据时，操作证件号码和手机号两个字段就会采用咱们自定义的序列化器，完成敏感信息脱敏功能。
脱敏数据反脱敏
对接前端的敏感数据脱敏展示功能做到上面这些就已经实现了。但是总感觉哪里不对，因为咱们在购票服务中，下单接口会调用乘车人详细信息接口获取到手机号、证件号等信息保存入库。
如果我在后端服务里去调用乘车人的信息接口，那岂不是也是脱敏的？这样的话，存储到数据库的数据就不准确了，期望是真实的数据，但是实际是脱敏后的。为此，我们需要想办法把自己脱敏后的数据还原回来，这里介绍几种思路：
Redis缓存原始数据
将脱敏后的数据和一个随机id一起封装为个对象一起传给前端，我在redis中以这个id为key，未脱敏值为value，当前端需要基于脱敏数据进行相关操作就传个id过来让我后端在redis找到该数据的原始态
这种方案比较适用于脱敏数据较少的情况，一般对于这种敏感数据展示的需求是比较少的，但是为了实现这么个反脱敏的操作我得浪费一大块缓存取时刻保持一份热点也许相对较小的数据，一个项目的用户量上来了，他们的手机号、身份证号等等敏感数据越来越多，那这样子缓存的占比也越来越大。
对称算法加解密
这种模式的脱敏就不是运用我们前面提到的替换操作，而是一种对称加解密的过程，将敏感数据采用一个对称算法加密后传输给前端，前端将其传入到后端后再凭借对称解密的方式还原原始数据。
这种方式优点在于对称加密算法可以提供较高的安全性，只有持有密钥的人才能解密敏感数据，降低了数据泄露的风险。并且对称加解密算法通常具有较高的执行效率，可以快速地对数据进行加解密操作。但是缺点也很明显，由于对称加解密方式是全盘加密和解密，无法对敏感数据进行细粒度的控制，比如只加密部分字段或片段。并且有被拦截通过一些工具进行解码风险，从而泄露数据。
总结
本文主要介绍了数据脱敏的相关内容，首先介绍了数据脱敏的概念，在此基础上介绍了常用的数据脱敏规则；随后介绍了本文的重点Hutool工具及其使用方法，在此基础上进行了实操，分别演示了使用DesensitizedUtil工具类、配合Jackson通过注解的方式完成数据脱敏；最后，介绍了一些常见的数据反脱敏方法，本文内容如有不当之处，还请大家批评指正。
