前言

        在实际项目开发中，我们经常会遇到一些金额计算，分摊等问题，通常我们都使用java.math.BigDecimal 来完成各种计算，避免使用浮点数float,double来计算金额，以免丢失精度，以下是博主部分使用场景和使用BigDecimal简记分享。。

案例1：统计各年龄段，用户存款：实现集合的所有金额相加，结果保留两位小数

        在平常项目中，我们经常会遇到查询某个集合，在集合下计算所有价钱的总和

 public static void main(String[] args) {//无论如何都会出现两位小数 java.math.BigDecimal.ROUND_HALF_UPList<User> userList = new ArrayStack();userList.add(new User().setAge(30).setMoney(new BigDecimal("145")).setUsername("dzx"));userList.add(new User().setAge(10).setMoney(new BigDecimal("143")).setUsername("dzx"));userList.add(new User().setAge(10).setMoney(new BigDecimal("144")).setUsername("dzx"));userList.add(new User().setAge(10).setMoney(new BigDecimal("142")).setUsername("dzx"));System.out.println(userList.stream().map(User::getMoney).reduce(BigDecimal.ZERO,BigDecimal::add).setScale(2, ROUND_HALF_UP));}

        此处我们使用了stream的处理方式，更简洁的计算了总和，设置精度为2，和四舍五入，关于ROUND_HALF_UP的其他取值，可以参考java.math.BigDecimal.ROUND_HALF_UP静态方法里的取值，共有0-7序号的8种取值，经常使用ROUND_HALF_UP=4（四舍五入）、ROUND_HALF_DOWN=5（五舍六入）、ROUND_FLOOR=3（向下取整）、ROUND_CEILING=2（向上取整）

案例2：用户下单谋些商品，商品购买的支付金额不准确（包含了各种优惠），需要重新分摊计算每件商品金额，分摊的算法就是通过每件商品的支付金额占比，计算出具体每件商品的实付金额

        通常我们需要分摊，总会出现除不尽，或者精度问题，为此我们要保证总的数不能少，为了减少精度等问题，就要采用最后一件做减法的方式，这样就能保证最后分摊金额的准确性。以图中为例，用户下单购买了三件商品，订单总实付为100.1，支付为233，由于各种原因（平台各种优惠，银行满减，红包等活动）经常导致支付金额与实付金额不等，那么就要重新计算各商品的实付金额

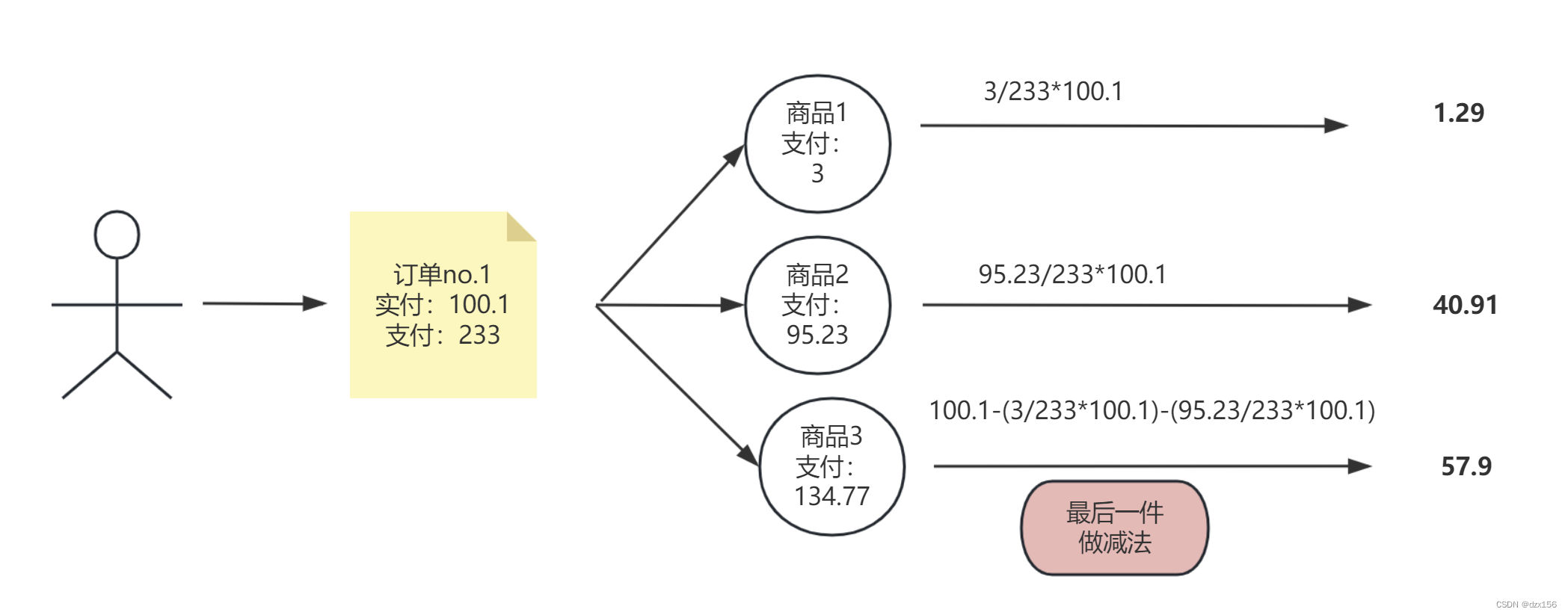
ps:图中计算结果都为四舍五入，保留小数两位，计算器计算的结果，非程序

        三件商品，其中商品1:支付3，那么就需要计算她的实付金额，首先需要计算这件商品原支付金额的占比，再通过这个比例计算实付金额，商品2同理，到商品3则要采用最后一件做减法的方式，否则会造成总的实付金额会不等的情况。具体计算以商品1为例，实付金额为：3/233*100.1=1.29，按照这样的逻辑编写代码

     public static void main(String[] args) {//先除再乘BigDecimal result1 = new BigDecimal("3").divide(new BigDecimal("233"),2,ROUND_HALF_UP).multiply(new BigDecimal("100.1")).setScale(2,ROUND_HALF_UP);System.out.println("先除再乘，输出："+result1);}

先除再乘，输出：1.00

        我们会发现程序实际计算结果,和程序计算结果有偏差，中间的偏差是哪里来的呢？答案是除法来的，我们在平常计算的时候，除以200的时候已经做了精度处理，因为我们不可能算的尽，因此我们的做法都是先乘后除,乘法为什么就不会有这个问题，因为乘法通常都是有限的数，非无穷的数，我们乘法可以避免进度丢失，因此我们实际计算的时候，需要调整计算公式，由3/233*100.1调整为3*100.1/200，具体代码如下：

      public static void main(String[] args) {//先乘再除BigDecimal result2 = new BigDecimal("3").multiply(new BigDecimal("100.1")).divide(new BigDecimal("233"),2,ROUND_HALF_UP).setScale(2,ROUND_HALF_UP);System.out.println("先乘再除，输出："+result2);}

先乘再除，输出：1.29

        这样我们会避免了除法除不尽带来的精度丢失问题，实际结果应该为1.29

        总结

         1.金额计算中，避免先除后乘精度丢失，应先乘后除

         2.金额分摊中，应该使用最后一件用减法的方式，分摊