个人主页:兜里有颗棉花糖
欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创
收录于专栏【手撕算法系列专栏】【LeetCode】
🍔本专栏旨在提高自己算法能力的同时,记录一下自己的学习过程,希望对大家有所帮助
🍓希望我们一起努力、成长,共同进步。
原题链接:点击直接跳转到该题目
目录
- 1️⃣题目描述
- 2️⃣题目解析
- 3️⃣解题代码
1️⃣题目描述
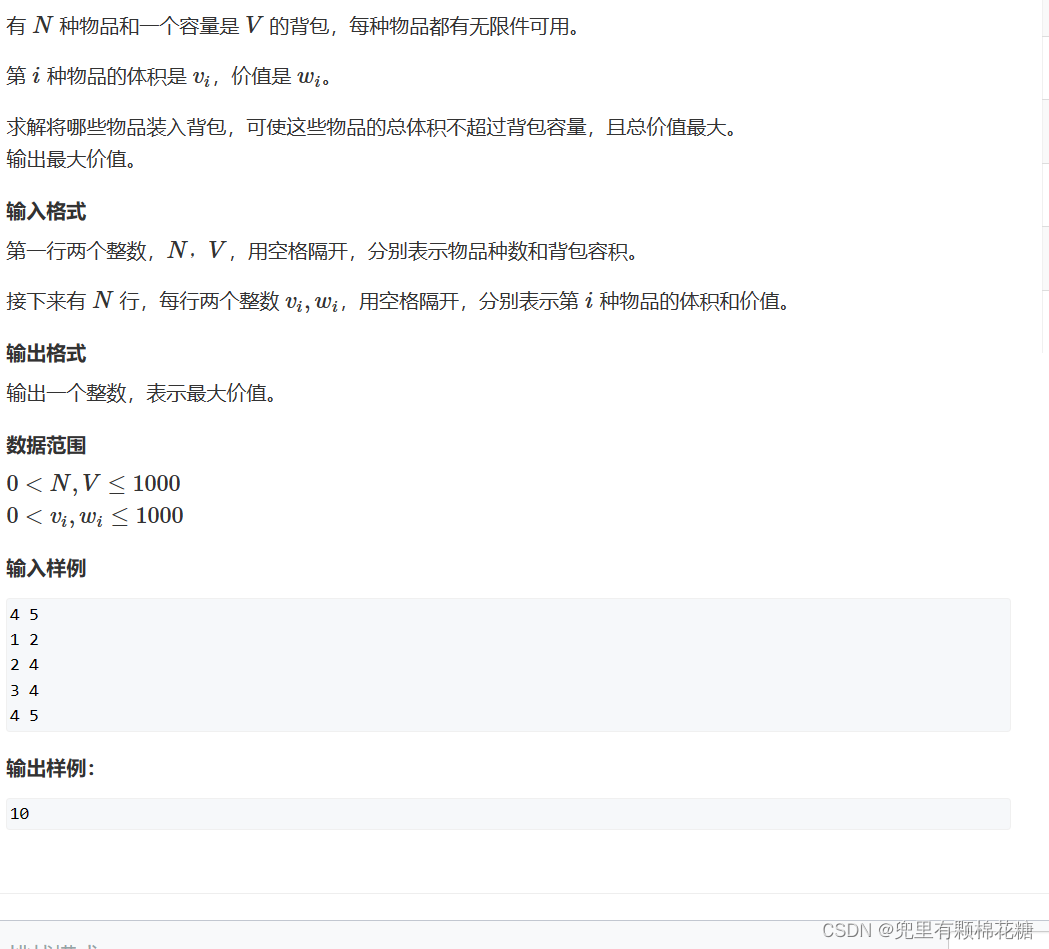
2️⃣题目解析
解法1:
状态表示:dp[i][j]表示从前i个物品中进行挑选体积不超过j的所有选法中的最大价值。
状态转移方程:
dp[i][j] = max(dp[i][j],dp[i - 1][j - V[i] * k] + k * W[i])
3️⃣解题代码
朴素算法:
#include<iostream>
using namespace std;const int N = 1010;
int V[N],W[N],dp[N][N];int main()
{int n,v;cin >> n >> v;for(int i = 1;i <= n;i++) cin >> V[i] >> W[i];for(int i = 1;i <= n;i++){for(int j = 0;j <= v;j++){for(int k = 0;k * V[i] <= j;k++){dp[i][j] = max(dp[i][j],dp[i - 1][j - V[i] * k] + k * W[i]); }}}cout << dp[n][v];return 0;
}
时间优化:
#include<iostream>
using namespace std;const int N = 1010;
int V[N],W[N],dp[N][N];int main()
{int n,v;cin >> n >> v;for(int i = 1;i <= n;i++) cin >> V[i] >> W[i];for(int i = 1;i <= n;i++){for(int j = 1;j <= v;j++){dp[i][j] = dp[i - 1][j];if(j - V[i] >= 0) dp[i][j] = max(dp[i - 1][j],dp[i][j - V[i]] + W[i]);}}cout << dp[n][v];return 0;
}
空间优化(滚动数组):
#include<iostream>
using namespace std;const int N = 1010;
int V[N],W[N],dp[N];int main()
{int n,v;cin >> n >> v;for(int i = 1;i <= n;i++) cin >> V[i] >> W[i];for(int i = 1;i <= n;i++)for(int j = V[i];j <= v;j++)dp[j] = max(dp[j],dp[j - V[i]] + W[i]);cout << dp[v];return 0;
}















)



)
![[架构之路-243]:目标系统 - 纵向分层 - 架构是表面轮廓、内部骨架、未来蓝图,企业组织架构、信息系统架构、软件架构、应用程序就架构](http://pic.xiahunao.cn/[架构之路-243]:目标系统 - 纵向分层 - 架构是表面轮廓、内部骨架、未来蓝图,企业组织架构、信息系统架构、软件架构、应用程序就架构)