
文章目录
- Abstract
- Introduction
- Related Work
- Residual Representations
- Shortcut Connections
- Deep Residual Learning
- Residual Learning
- Identity Mapping by Shortcuts
- Experiment
- Conclusion
原文链接
Abstract
深层的神经网络更难训练,我们提出了一个残差学习框架,以简化比以前使用的网络深度大得多的网络的训练。我们明确地将层重新表述为参考层输入的学习残差函数,而不是学习未参考的函数。我们提供了全面的经验证据,表明这些残余网络更容易优化,并且可以从相当大的深度提高精度,解决了层数变深误差在训练集测试集都增大问题
Introduction
深度卷积神经网络[22,21]在图像分类方面取得了一系列突破[21,49,39]。深度网络自然地以端到端的多层方式集成低/中/高层特征[49]和分类器,并且特征的“级别”可以通过堆叠层的数量(深度)来丰富。
最近的证据表明网络深度至关重要,在深度的重要性的驱使下,一个问题出现了:学习更好的网络就像堆叠更多的层一样简单吗?回答这个问题的一个障碍是臭名昭著的梯度消失/爆炸问题[14,1,8],它从一开始就阻碍了收敛。这个问题已经通过规范化初始化[23,8,36,12]和中间规范化层在很大程度上得到了解决
当更深的网络能够开始收敛时,一个退化问题就暴露出来了:随着网络深度的增加,精度趋于饱和(这可能不足为奇),然后迅速退化。出乎意料的是,这种退化并不是由过拟合引起的,在适当深度的模型上添加更多的层会导致更高的训练误差,这一点在[10,41]中有报道,我们的实验也充分验证了这一点。图1是一个典型的例子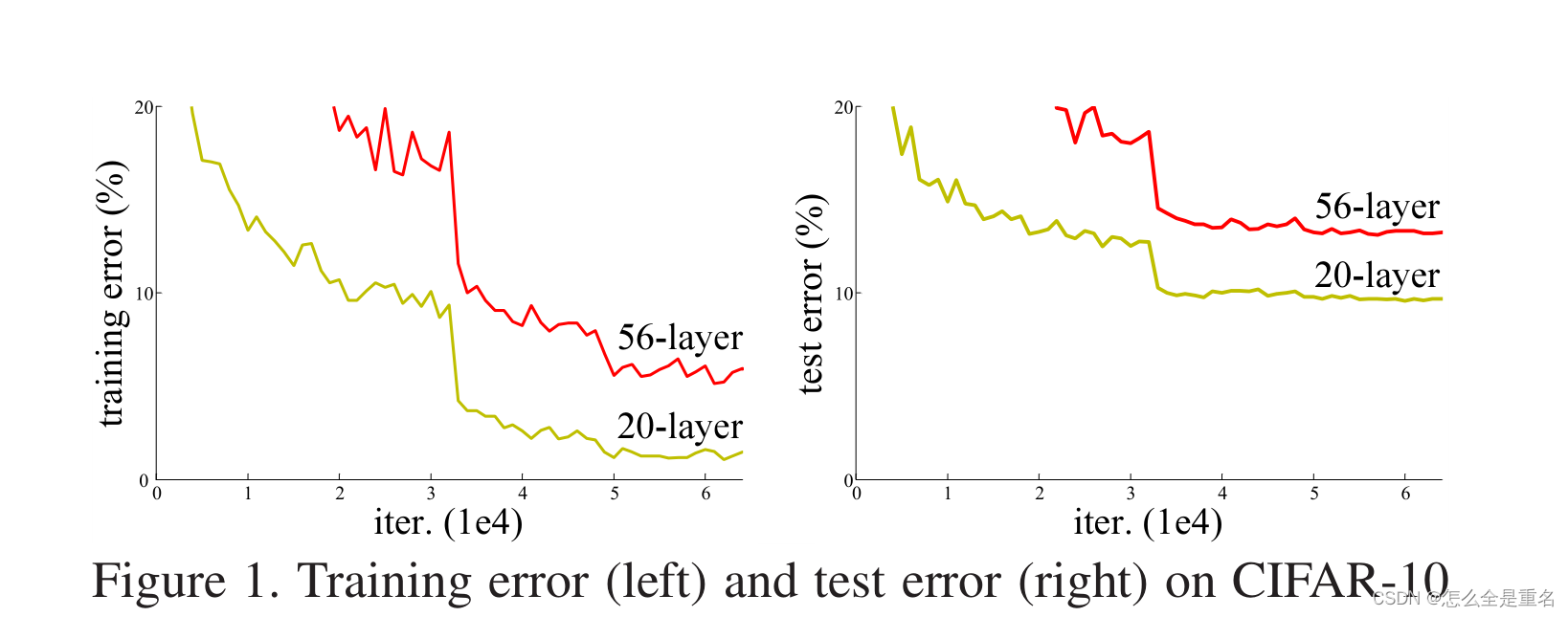
在本文中,我们通过引入深度残差学习框架来解决退化问题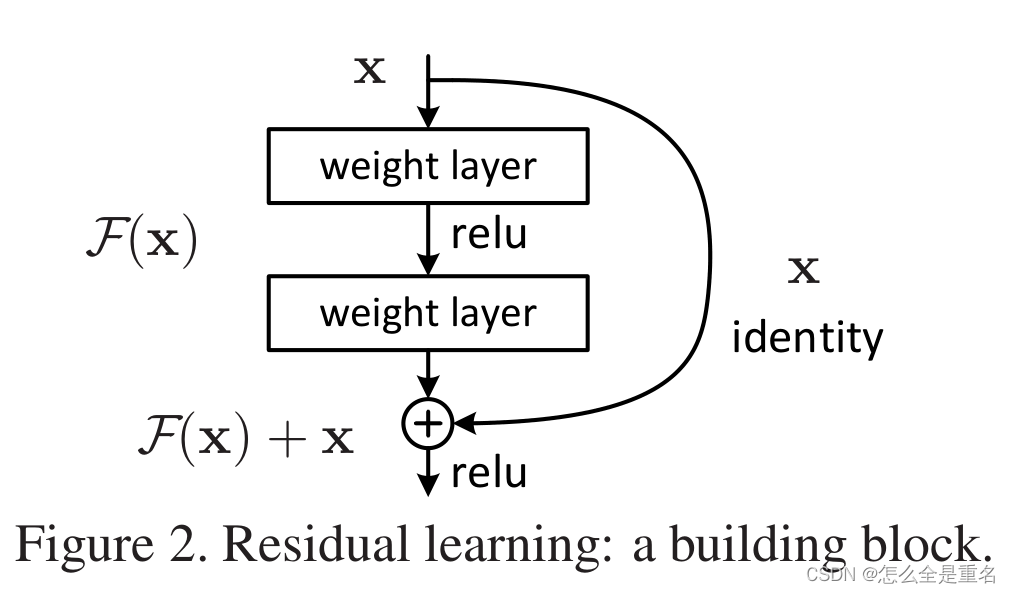
形式上,将期望的底层映射表示为H(x),我们让堆叠的非线性层适合F(x)= H(x) - x的另一个映射,原始映射被重新映射为F(x)+x
F(x)+x的表达式可以通过具有“快捷连接”的前馈神经网络来实现,在我们的例子中,快捷连接只是执行身份映射,它们的输出被添加到堆叠层的输出中(图2)。身份快捷连接既不增加额外的参数,也不增加计算复杂性,整个网络仍然可以通过反向传播的SGD进行端到端训练,并且可以使用通用库(例如Caffe[19])轻松实现,而无需修改求解器。
我们发现:1)我们的极深残差网络很容易优化,但对应的“普通”网络(简单地堆叠层)在深度增加时表现出更高的训练误差;2)我们的深度残差网络可以很容易地从深度的大大增加中获得精度的提高,产生的结果比以前的网络要好得多
进行了一系列实验,取得了非常好的结果。。。极深表征在其他识别任务上也有出色的泛化性能,并使我们在ILSVRC & COCO 2015竞赛中进一步在ImageNet检测、ImageNet定位、COCO检测和COCO分割方面获得第一名
Related Work
Residual Representations
VLAD、Multigrid等方法表明,良好的重新配方或预处理可以简化优化过程
Shortcut Connections
与我们的研究同时进行的还有“highway network”[41,42],它们具有门控功能,提供了快捷连接
这些门是数据依赖的,有参数,而我们的身份快捷方式是无参数的
我们的公式总是学习残差函数;我们的身份快捷键永远不会关闭,所有的信息总是通过附加的残余函数来学习
Deep Residual Learning
Residual Learning
把H(x)看作是由几个堆叠层(不一定是整个网络)拟合的底层映射,其中x表示这些层的第一层的输入。如果假设多个非线性层可以渐近逼近复杂函数,那么等价假设它们可以渐近逼近残差函数,即H(x)−x(假设输入和输出具有相同的维数)
因此,我们不是期望堆叠层近似于H(x),而是明确地让这些层近似于残差函数F(x):= H(x) - x。因此,原始函数变为F(x)+x。尽管这两种形式都应该能够渐进地逼近所需的函数(如假设的那样),但学习的难易程度可能不同
正如我们在引言中讨论的那样,如果添加的层可以被构造为身份映射,那么较深的模型应该具有不大于其较浅的对应部分的训练误差。通过残差学习的重新表述,如果恒等映射是最优的,求解器可以简单地将多个非线性层的权值向零驱动,从而逼近恒等映射
Identity Mapping by Shortcuts
我们对每几个堆叠层采用残差学习,构建块如图2所示。在本文中,我们认为构建块定义为
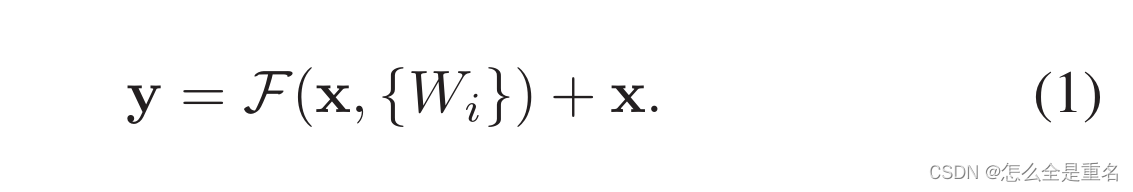
x和y是所考虑的层的输入和输出向量。函数F(x,{W i})表示待学习的残差映射,W是权重
对于图2中有两层的例子,F = W2σ(W1x),其中σ表示Relu,为了简化表达式,省略了偏差,操作F + x是通过一个快捷连接和元素加法来执行的。我们采用加法后的第二个非线性(即σ(y),见图2)
x和F的维数在Eqn(1)中必须相等。如果不相等(例如,当改变输入/输出通道时),我们可以通过快捷连接执行线性投影Ws来匹配维度: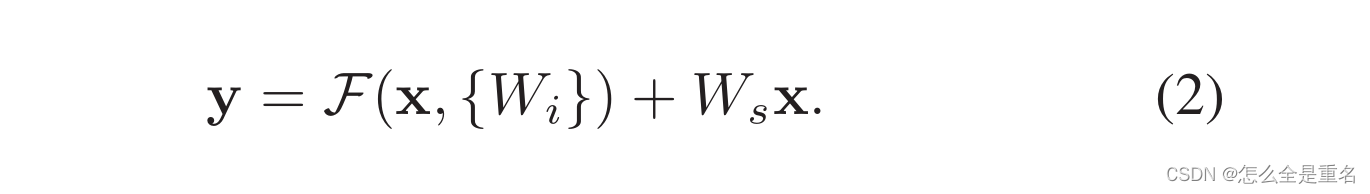
我们还注意到,尽管为了简单起见,上面的符号是关于全连接层的,但它们适用于卷积层。函数F(x,{W i})可以表示多个卷积层,逐个通道地在两个特征映射上执行逐个元素的加法
Experiment
在ImageNet数据集上,我们评估了深度高达152层的残差网络,是VGG网络[40]深度的8倍,但仍然具有较低的复杂性。这些残差网络的集合在imagenet测试集上的误差达到3.57%,这一结果是对ILSVRC 2015分类任务的第一次验证,我们还介绍了100层和1000层的CIFAR-10分析。表征的深度对于许多视觉识别任务至关重要,仅由于我们的极深表示,我们在COCO对象检测数据集上获得了28%的相对改进
Conclusion
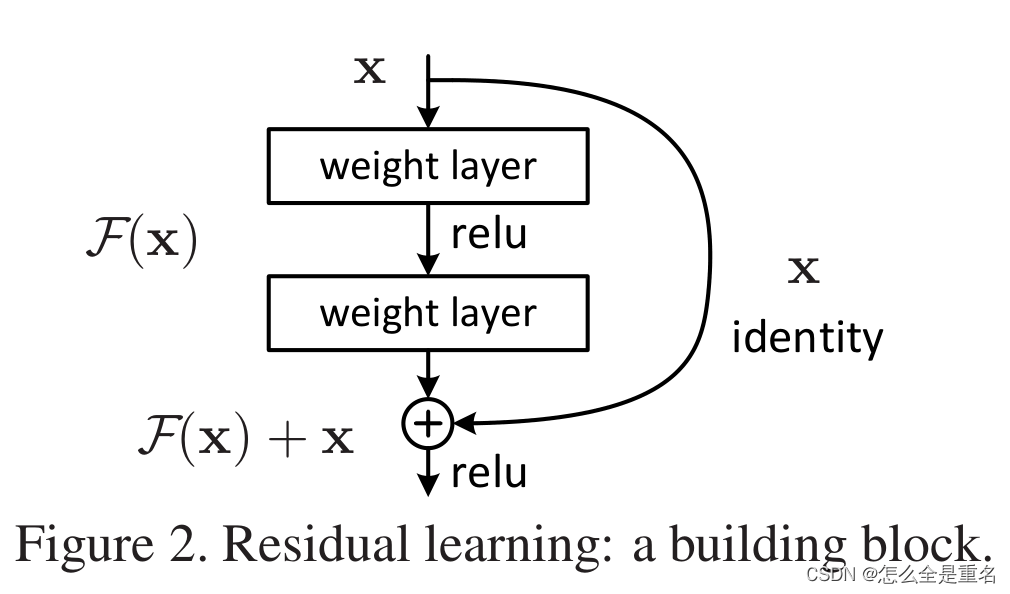
x是原来训练好的参数,我们现在期望的是H(x),不用ResNet的话,模型会直接学习H(x),但ResNet会学习残差函数F(x),
F(x)=H(x)-x,即ResNet学习的是训练的与真实的差距,也可以理解为ResNet在学习模型与真实值之间的差距。
原始做法是不断优化H(x),而ResNet是不断优化F(x)即训练与真实之间的差距,最终输出的是F(x)+x,即根据identity mapping的思想,x不变,而差距越来越小,因此网络越深不会导致训练结果越来越差







)
删除排序数组中的重复项)



)






