回溯是最重要的算法思想之一，主要解决一些暴力枚举也搞不定的问题，比如：组合、分割、子集、排列、棋盘等。从性能角度来看回溯算法的效率并不高，但对于这些暴力都搞不定的算法能出结果就很好了，效率低点没关系。

认识回溯思想

回溯可以视为递归的拓展，很多思想和解法都和递归密切相关。因此学习回溯时，对于递归来分析其特征会理解更深刻。

关于递归和回溯的区别，设想一个场景，某猛男想脱单，现在有两种策略：

1. 递归策略：先于意中人制造偶遇，然后了解人家的情况，然后约吃饭，有好感后尝试拉手，没有拒绝就表白。
2. 回溯策略：先统计周围所有的单身女孩，然后一个一个表白，被拒绝就说”我喝醉了“，然后就当啥也没发生，继续找下一个。

其实回溯本质就是这么个过程。

回溯最大的好处：有非常明确的模版，所有的回溯都是一个大框架，因此透传理解回溯的框架是解决一切回溯问题的基础。那么就来分析这个框架。

回溯不是万能的，而且能解决的问题也非常明确，比如：组合、分割、子集、排列、棋盘等，不过这些问题具体处理时又有很多不同，需要具体问题具体分析。

回溯可以理解为递归的拓展，而代码结构又特别像 深度遍历 N 叉树，因此只要知道递归，理解回溯并不难。难在很多人不理解为什么在递归语言之后要有个”撤销“的操作。可以假设一个场景：你谈了个新女朋友，来你家之前，你是否会将你前任的东西赶紧藏起来？回溯也是一样，有些信息是前任的，要先处理掉才能重新开始。

回溯的代码框架

func Backtracking(参数) {if 终止条件 {存放结果return}for 选择本层集合中元素（画成树，就是树节点孩子的大小） {处理节点Backtracking()回溯，撤销处理结果}
}

从 N 叉树说起

先看一下 N 叉树遍历的问题，二叉树的前序遍历，代码如下：

/*** Definition for a binary tree node.* type TreeNode struct {*     Val int*     Left *TreeNode*     Right *TreeNode* }*/
func preorderTraversal(root *TreeNode) []int {ret := make([]int, 0)if root == nil {return ret}ret = append(ret, root.Val)ret = append(ret, preorderTraversal(root.Left)...)ret = append(ret, preorderTraversal(root.Right)...)return ret
}

假如现在是一个三叉、四叉甚至 N 叉树该怎么办呢？很显然这时候就不能用 Left 和 Right 来表示分支了，使用一个切片比较好，就是这样：

/*** Definition for a Node.* type Node struct {*     Val int*     Children []*Node* }*/func preorder(root *Node) []int {ret := make([]int, 0)if root == nil {return ret}ret = append(ret, root.Val)for _, v := range root.Children {ret = append(ret, preorder(v)...)}return ret
}

到这里，有没有发现和上面说的回溯的模版非常像了？是的！非常像！既然很像，那说明两者一定存在某种关系。继续往下看

有的问题暴力搜索也不行

我们说回溯主要解决暴力枚举也解决不了的问题。
看个例子：题目链接：LeetCode-77. 组合

对于示例1，写成代码很容易，双层循环轻松搞定：

func combine(n int, k int) [][]int {ret := make([][]int, 0)for i:=1; i<=n; i++ {for j:=i+1;j<=n;j++ {arr := []int{i, j}ret = append(ret, arr)}}return ret
}

假如 k 变大，比如 k=3 呢？也可以，三层循环基本搞定：

func combine(n int, k int) [][]int {ret := make([][]int, 0)for i:=1; i<=n; i++ {for j:=i+1;j<=n;j++ {for u:=j+1;u<=n;u++ {arr := []int{i, j, u}ret = append(ret, arr)}}}return ret
}

如果这里的 k=5 呢，甚至 k=50 呢？你需要套多少层循环？甚至告诉你 k 就是一个未知的正整数 k，你怎么写循环呢？这时候已经无能为力了，所以暴力搜索就不行了。

这就是组合类型问题，除此之外 子集、排列、切割、棋盘 等方面都有类似的问题。

回溯 = 递归 + 局部枚举 + 放下前任

继续研究 题目链接：LeetCode-77. 组合 ，图示一下上面自己枚举所有答案的过程。

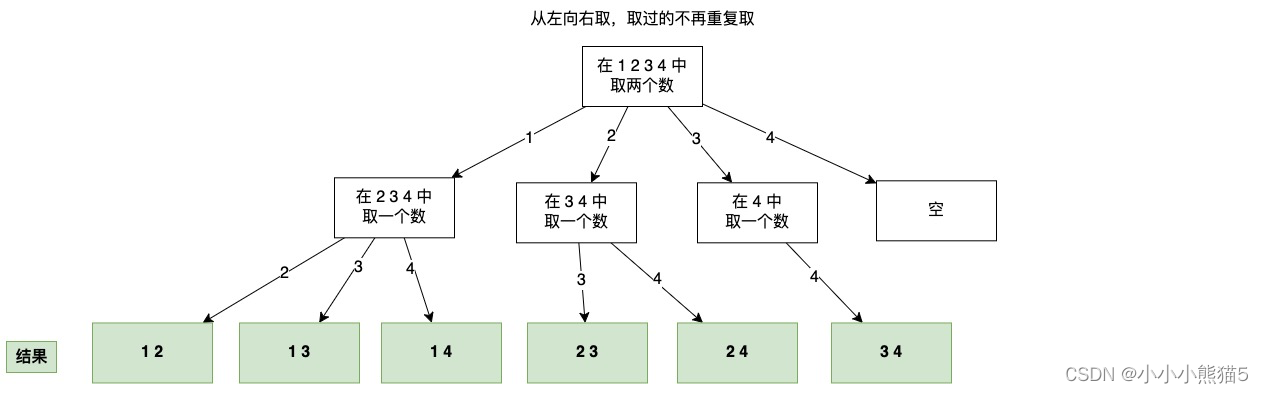
每次从集合中选取元素，可选择的范围会逐步收缩，到了取 4 时就直接为空了。

观察树结构，可以发现，每次访问到一次叶子节点（图中绿色框），就找到了一个结果。虽然最后一个是空的，但是不影响结果。这相当于只需要把根节点开始每次选择的内容（分支）达到叶子节点时，将其收集起来就是想要的结果。

元素个数 n 相当于树的宽度（横向），每个结果的元素个数 k 相当于树的深度（纵向）。所以我们说回溯算法就是一纵一横而已。再分析其他规律：

1. 每次选择都是从类似「1 2 3 4」，「2 3 4」这样的序列中一个个选的，这就是局部枚举，而且越往后枚举范围越小。
2. 枚举时，就是简单的暴力测试，一个个验证，能否满足要求，从上图可以看到，这就是 N 叉树遍历的过程，因此两者代码必然很像。
3. 从图可见，每个子树都是个可以递归的子结构。

这样我们就将回溯与 N 叉树完美结合在一起了。

但是，还有一个大问题：回溯一般会有个手动撤销的操作，为什么呢？继续观察上图：

可以发现，收集每个结果不是针对叶子节点，而是针对树枝的，比如最上层首先选了 1， 下层如果选2，结果就是「1 2」，如果下层选了3，结果就是「1 3」，依此类推。现在问题是当得到第一个结果「1 2」之后，怎么得到第二个结果「1 3」呢？

可以发现，可以在得到「1 2」之后将 2 撤销，再继续取3，这样就得到了「1 3」，同理可以得到「1 4」，之后当前层就没有了，可以将 1 撤销，继续从最上层取 2 继续进行。
对应的代码操作：就是先将第一个结果放在临时列表 path 里，得到第一个结果「1 2」之后就将 path 里的内容放进结果列表中，之后，将 path 里的 2 撤销，继续寻找下一个结果「1 3」，然后继续讲 path 放入结果，然后再撤销继续找。

Go代码【LeetCode-77. 组合】

题目链接：LeetCode-77. 组合

func combine(n int, k int) [][]int {ret := make([][]int, 0)if k <= 0 || n < k {return ret}path := make([]int, 0)var dfs func(int)dfs = func(start int) {if len(path) == k {// 关键pathcopy := make([]int, k)copy(pathcopy, path)ret = append(ret, pathcopy)return}for i:=start;i<=n;i++ {path = append(path, i)dfs(i+1)path = path[:len(path)-1]}}dfs(1)return ret
}

回溯热身-再论二叉树的路径问题

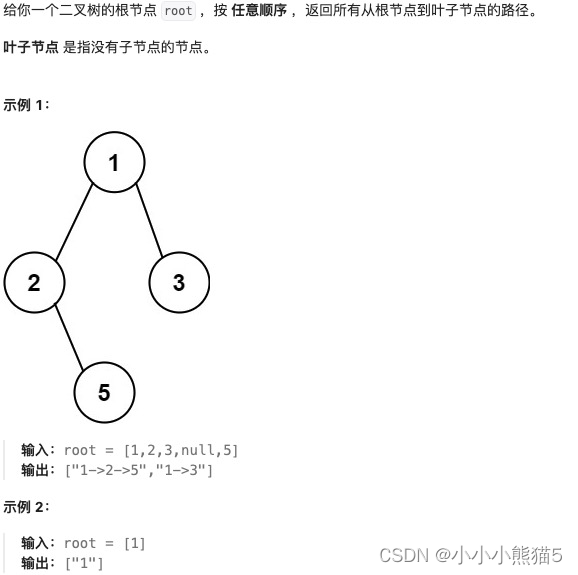
题目：二叉树的所有路径

题目链接：LeetCode-257. 二叉树的所有路径

Go 代码

/*** Definition for a binary tree node.* type TreeNode struct {*     Val int*     Left *TreeNode*     Right *TreeNode* }*/
func binaryTreePaths(root *TreeNode) []string {ret := make([]string, 0)if root == nil {return ret}path := make([]int, 0)var dfs func(*TreeNode)dfs = func(node *TreeNode){if node == nil {return}path = append(path, node.Val)if node.Left == nil && node.Right == nil {ret = append(ret, conv(path))path = path[:len(path)-1]return}dfs(node.Left)dfs(node.Right)path = path[:len(path)-1]}dfs(root)return ret
}
func conv(arr []int) string {length := len(arr)strarr := make([]string, length)for i, v := range arr {strarr[i] = strconv.Itoa(v)}return strings.Join(strarr,"->")
}

对比之前递归方式的写法（没有撤回步骤，不是回溯写法）

/*** Definition for a binary tree node.* type TreeNode struct {*     Val int*     Left *TreeNode*     Right *TreeNode* }*/
func binaryTreePaths(root *TreeNode) (res []string) {if root == nil {return nil}var a func(*TreeNode, string)a = func(node *TreeNode, path string) {if node == nil {return}str := fmt.Sprintf("%d", node.Val)path = path+str// 叶子节点if node.Left == nil && node.Right == nil {res = append(res, path)return}a(node.Left, path+"->")a(node.Right, path+"->")}a(root, "")return
}

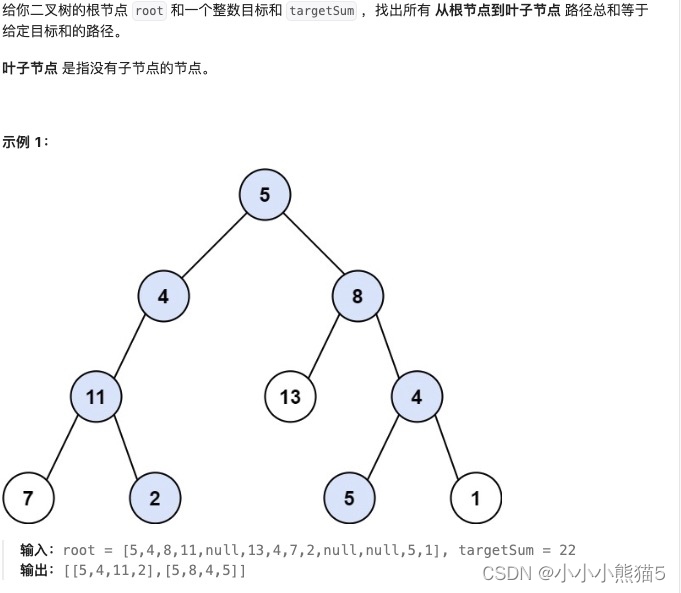
题目：路径总和 II

题目链接：LeetCode-113. 路径总和 II

Go 代码

/*** Definition for a binary tree node.* type TreeNode struct {*     Val int*     Left *TreeNode*     Right *TreeNode* }*/
func pathSum(root *TreeNode, targetSum int) [][]int {ret := make([][]int, 0)if root == nil {return ret}path := make([]int, 0)var dfs func(*TreeNode, int)dfs = func(node *TreeNode, sum int) {if node == nil {return}path = append(path, node.Val)// 叶子节点if node.Left == nil && node.Right == nil {// 路径匹配，加入结果列表if node.Val == sum {pathcopy := make([]int, len(path))copy(pathcopy, path)ret = append(ret, pathcopy)}path = path[:len(path)-1]return}dfs(node.Left, sum-node.Val)dfs(node.Right, sum-node.Val)path = path[:len(path)-1]}dfs(root, targetSum)return ret
}