2023年6月22日，诺贝尔经济学奖得主哈里.马克维茨于美国去世，享年95岁。

作为现代金融先驱者，马科维茨不仅是将数学引入金融的第一人，更用数学解释了分散投资的重要性。

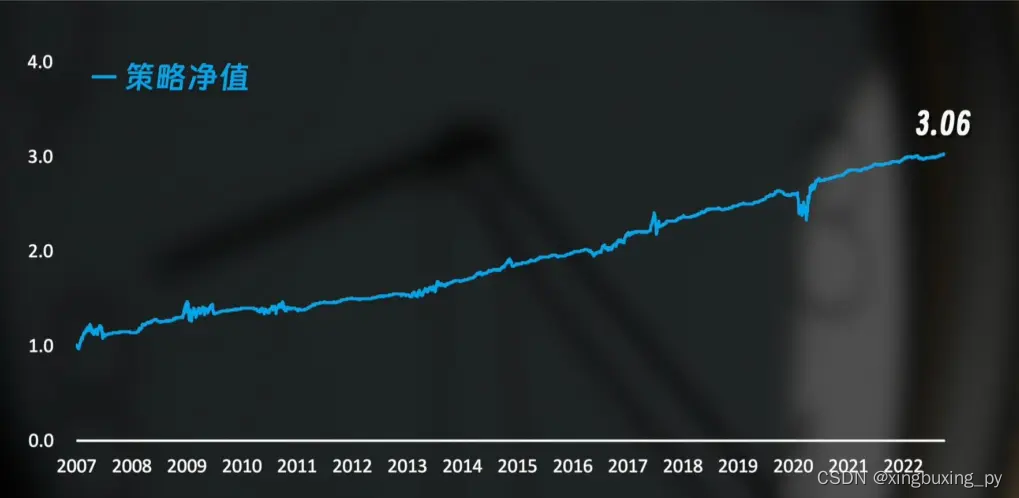
更令人惊叹的是，过去十几年中如果按他的理论在中证1000、标普500等指数上进行投资和仓位分配，将会得到这样一条资金曲线：

01 马科维茨传奇

1 故事伊始

1950年，本科学哲学的马克维茨在芝加哥大学跨界读经济学博士。身为气运之子，他开局就拿到了爽文男主的剧本。

他的导师配置在任何时代都堪称T0级别：

他的际遇也令人称奇。某次马科维茨为了博士论文选题去找老师马尔沙克，在办公室门口等待时遇到了一个股票交易员。

闲聊中交易员建议马科维茨去研究股票市场，这引起了他的兴趣。

在和马尔沙克充分讨论后，他决定今后致力于将数学和统计学的方法运用于股票市场。

2 资产组合理论

在一众大牛老师的支持下，马科维茨左手概率论、右手运筹学，开天辟地头一回的将数学引入了投资领域。

于1952年祭出大杀器论文《资产组合的选择》。

这篇论文主要教你如何进行资产选择，也就是如何仓位分配，说白了就是教你应该买什么。

它被认为是现代投资组合理论的开山之作，绝大部分投资机构的资产组合都受益于此，被誉为“华尔街的第一次革命”。

有趣的是，在论文答辩中由于不断强调数学在股票市场的应用，他的导师弗里德曼甚至觉得他的研究不属于经济学或统计学。

那时的马科维茨慌得一批，害怕无法毕业。

但现在我们已经知道，他的论文确实不属于这两个学科，因为他早已在不经意间开创了一门新的学科：现代金融学。

最后就像所有爽文的结尾，凭借资产组合理论，马克维茨于1990年在众望所归下获得了诺贝尔经济学奖。

02 资产组合理论

1 股票分仓

假设投资者小胡准备了10万元炒股，初入股市的他在A股挑了3只股票作为投资标的。

该如何分配这3只股票的仓位？

将资金分成3份每股买3.3万？还是有的股票多买点，有的股票少配点？

当初马克维茨解决的就是类似问题。

我们也正好借助这个问题，给大家简单介绍一下马克维茨的资产组合理论。

2 量化收益

假设选出的3只股票分别是A、B、C。

其中股票A有一半的概率在未来一年上涨20%，有一半的概率上涨10%，它的期望收益则为15%。

期望：试验中每次可能的结果乘以其结果概率的总和

若持有股票B一年后各有一半的概率上涨60%及下跌20%；股票C则有概率上涨100%或下跌50%。我们同样可以计算出对应的期望收益。

具体结果如图所示：

如在A/B/C中选择一只买入并持有，在不能加杠杆的情况下你会选哪个？

选择A的人相对保守，虽然赚的少，但胜在风险低，任何情况下都能稳赚不亏。

选B也不错，差的时候会亏20%，但好的情况却能赚60%。

选C就是富贵险中求了。虽然腰斩的风险高，但翻倍的诱惑巨大，汝之蜜糖彼之砒霜。

前面选择股票的过程，我们就是在权衡收益和风险，希望投资的收益更高，风险更低。

然而事与愿违，金融/人生的第一定律，就是高收益和低风险不可兼得。

我们往往只能根据自己的偏好，在收益和风险间进行权衡，做出最优选。

比如我们用了期望收益来量化收益，又该用什么方式来量化风险呢？

3 量化风险

马克维茨用的是方差（通常被用来描述一组数据的离散程度）。

股票市场中资产收益的离散程度就是风险。它的收益波动越大，方差越大，则风险越大。

通过计算我们发现股票A的方差是0.0025：

同理得出股票B/C的方差分别是0.16和0.5625。

综上所述，股票C的期望收益和风险是最高的，股票B次之，股票A最低。

这也佐证了金融学第一定律：风险和收益成正比。

03 组合收益与风险

1 股票组合

我们重新来看选择股票A/B/C的问题。

可能前面有很多同学选择了买入股票B，因为它比A赚的多又比C风险小。

但其实还有更好的选择。

比如把所有钱一分为二，各自买入股票A和C形成一个组合。

该组合在一年后的收益有下列四种情况：

它的期望收益和方差就如图所示：

组合的期望收益为20%，与股票B一致。但方差约为0.14，略小于股票B(0.16)。

即我们通过股票A和C构建了一个收益与股票B相同，但风险却更小的投资组合。此时股票B便已不再是最优解。

这就是投资组合的威力，通过组合我们可以找到比只买入单个股票更优的选择。

2 寻找最优组合

前面我们只是简单的平均分配资金买入A和C就得到了超过股票B的投资组合。

是否存在其他仓位分配模式使组合在20%的期望收益下风险最小？

又或方差在0.1的风险下，怎么在三只股票里分配仓位才能保证期望收益最大化？

如果你能在1950年回答上述问题，那你同样有获得诺贝尔经济学奖的潜质。

04 仓位分配策略

1 仓位分配

前面我们提出的股票仓位分配问题，其实就是1952年马克维茨解决的问题。

他在考虑股票相关性的情况下，运用标准凸二次规划解决了这个问题。

相关方法都在他的论文中，感兴趣的可以自己去查阅相关资料，也可以在评论区留言问我要了pdf和我交流。

具体方法我们就不做详细的讲解了，真讲了我怕大家犯困，毕竟是数学问题。

但不管怎样，马科维茨的资产组合理论来头再大、拿了再多奖项，如果对交易实战没有帮助的话，对我们而言就没有任何意义。

下面我们就借助历史数据和Python代码，来验证用他的理论进行仓位分配能不能赚钱。

2 仓位策略

假设各位富佬有一大笔钱要投资并选中了以下标的：

这些标的比较分散，包括了全球主流资产。该如何分配它们的仓位呢？

根据马科维茨的模型，我们需要知道这些标的未来一年的期望收益及方差。

可这些是未来发生的事，现在不可能知道。

所以实战中我们通常会用过去一段时间的数据来做估算。

比如在每月最后一个交易日，根据过去6个月资产的历史数据计算出每个资产的收益、方差及相关系数。

将这些数据作为参数套入模型中，计算出每个标的的仓位。

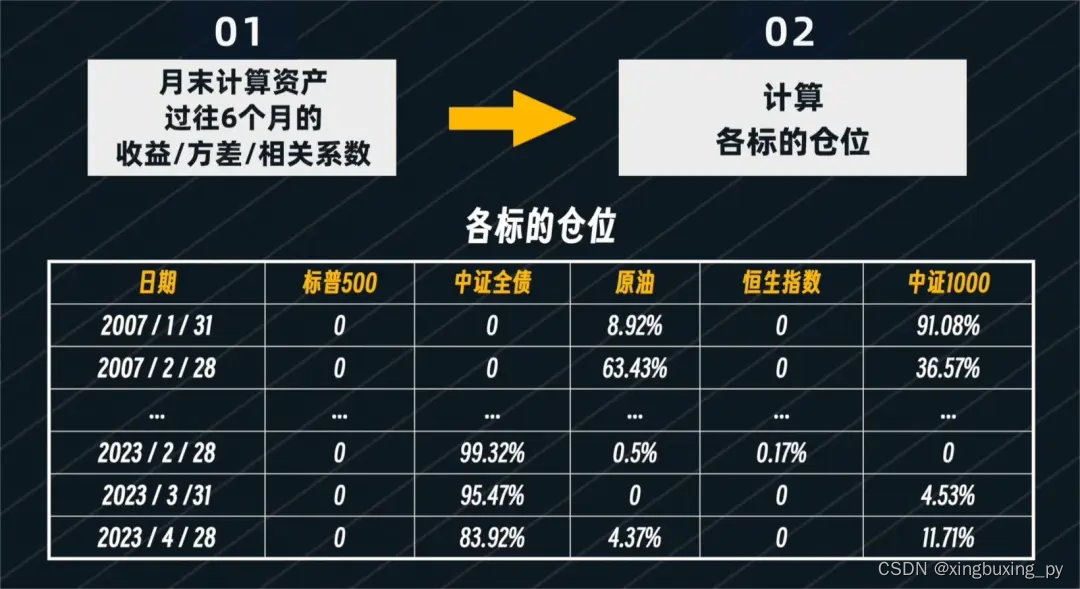
再按仓位买入这些指数并持有下个月整月。等下月末再按此法进行调整，如此循环往复。

大家不要觉得拿过去收益代替未来很可笑，或认为每月换仓很原始。

华尔街的投行精英之前都这么做，70年代计算机未普及时，他们还雇佣了很多人手工计算相关结果，甚至还出了专门的机械式计算器来加速计算。

知道了策略如何运行，我们又找来了这些指数的历史数据，并借助Python代码构建了对应的模型。

如果你对这个数据和代码感兴趣的话，可以在评论区留言，都是可以直接发给你的。

3 回测结果

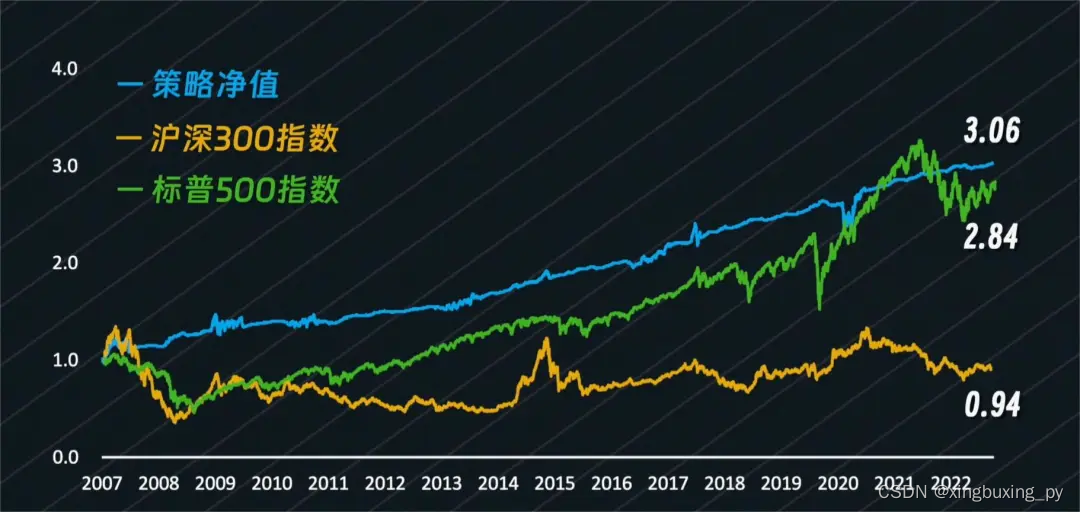
程序运行结果如图所示：

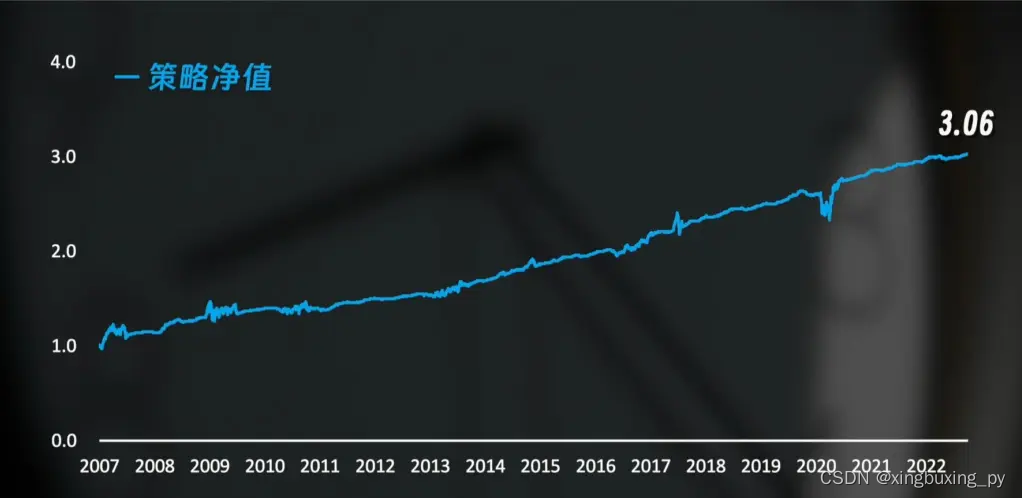
代表策略的蓝色曲线从2007年初的1块钱涨到了现在的3.06，年化收益7.28%，最大回撤仅14.38%（2020年黑天鹅时间事件）。

虽然年化收益并不算高，但长期来看不仅跑赢了长年3000点的大A，也跑赢了持续上涨的美股。

这样的策略你觉得适合去实盘吗？我个人还是比较推荐的。

它本质上是帮你在各种大类资产中分配仓位，实际操作也很简单，一月一次即可。

马科维茨的资产组合理论拿到诺奖也算是实至名归，毕竟他的理论在业界真的被广泛使用了。