RNN无法处理长距离依赖问题,通俗点就是不能处理一些较长的序列数据,那么今天就来介绍一下两个能处理长距离依赖问题地RNN变种结构,LSTM和GRU。
1. LSTM(Long short-term memory)
1.1 LSTM结构
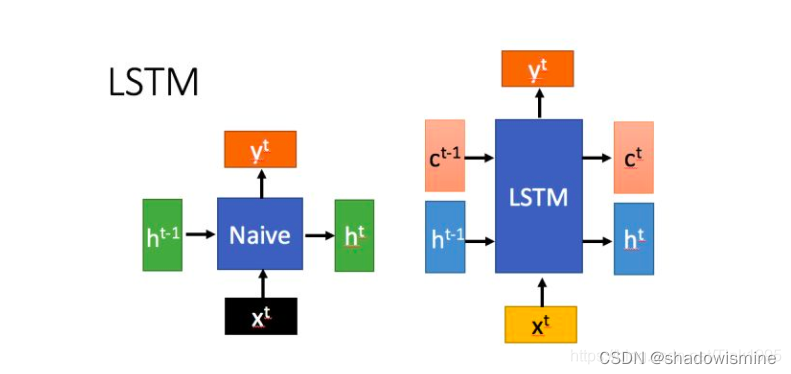
上左图是普通RNN结构图,上右图是LSTM结构图。
从图中我们可以看出,普通的RNN在隐藏层中只传递一个状态值h,而LSTM不仅传递h,还新增了一个状态值C,每一层隐藏层中的每一个神经元都接收上一时刻传递的h{t-1}和c{t-1},经过计算得到h{t}和c{t}再传入下一时刻。
那么接下来咱们就来看看状态c和h究竟在LSTM的隐藏层中做了哪些计算又是怎么传递地。
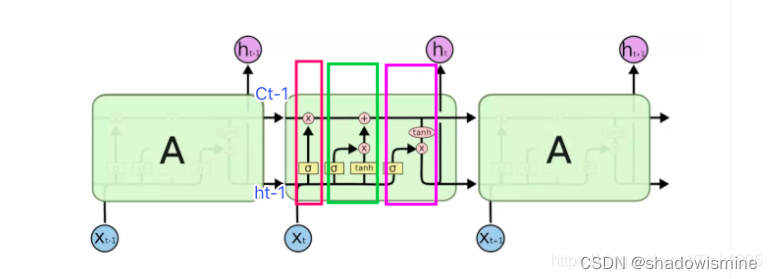
上图是LSTM的某一隐藏层的局部结构,三个矩形为{t-1},{t},{t+1}三个时刻的神经元,中间显示的是t时刻神经元的内部结构图。说实话只是单单看图的话,反正我当时是一脸懵逼,这都是些啥?不过不要慌,接下来咱们一步一步慢慢说明。
首先LSTM是由三个门来控制信息传递状态地,分别是红色方框对应的”忘记门“,绿色方框对应的”输入门“,和紫色方框对应的”输出门“。这三个门中一共包含3个sigmoid函数和2个tanh函数。使用sigmoid函数的原因是sigmoid函数能够将输入映射到[0,1]空间中,那么咱们就可以根据映射之后的概率对于上一时刻传递的信息进行有选择的去除,保留和输出。比如sigmoid函数的值为1也就是门的全开状态,则代表所有的信息都被保留,如果sigmoid函数为0也就是门的全闭状态,则代表所有的信息都不被保留。使用tanh函数是为了对数据进行处理,映射到[-1,1]的空间,当然也可以使用其他的激活函数,比如ReLU,至于效果谁好谁坏,我没有深究过,有研究表明在LSTM层数比较少的时候使用tanh比ReLU效果好。知道了这些之后,接下来咱们就来将这三个门一步一步拆解来讲讲具体这三个门中怎么计算。
忘记门:
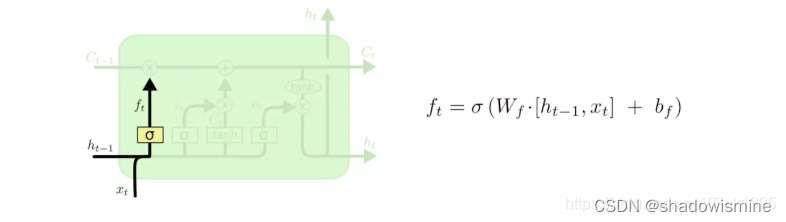
上图就是”忘记门“的结构,以及计算公式。说白了就是把t-1时刻传入的h{t-1}与t时刻的输入Xt进行拼接,然后通过权值矩阵Wf转换后,加上偏置bf,再由sigmoid函数映射到[0,1]空间中。就形成了这个”忘记门“。
然后通过”忘记门“ft对于上一时刻传入的C{t-1}进行有选择的忘记,将C{t-1}与ft进行点乘,得到去除一些信息后的”忘记门的输出“
输入门:

上图是”输入门“的结构,与”忘记门“类似,首先把t-1时刻传入的h{t-1}与t时刻的输入Xt进行拼接,然后通过权值矩阵Wi转换后,加上偏置bi,再由sigmoid函数映射到[0,1]空间中形成了这个”输出门“。然后得到输入数据,输入数据是把t-1时刻传入的h{t-1}与t时刻的输入Xt进行拼接,然后通过权值矩阵WC转换后,加上偏置bC,再有激活函数tanh映射到[-1,1]空间,得到输入数据Ct’。然后将"输入门"it与Ct’进行点乘,就能得到"输入门"的输出了。
得到Ct:
然后将”忘记门“的输出值与”输入门“的输出值加起来,就得到了t时刻的Ct值。

Ct中保留了t-1传入的部分信息和t时刻传入的经过筛选后的信息。得到了Ct,那咱们就只剩下计算t时刻的ht了,计算ht由”输出门“来完成。
输出门:

可以看到上图中的”输出门“的结构和计算公式,把t-1时刻传入的h{t-1}与t时刻的输入Xt进行拼接,然后通过权值矩阵Wo转换后,加上偏置bo,再由sigmoid函数映射到[0,1]空间中形成了这个”输出门“。
然后将上一步计算得到的Ct经过tanh函数缩放,映射到[-1,1]空间中,再与”输出门“点乘,就能得到输出门的输出值ht了。
这样咱们就计算出来t时刻的所有输出值,ht和Ct,然后ht和Ct又可以传入到下一时刻来进行循环操作了。
计算t时刻的输出yt:

1.2 LSTM 为什么能解决RNN的梯度消失问题?
好了,虽然上面说了那么多,可能小伙伴们也知道了LSTM的结构,但是我还是不明白啊,为什么这样的LSTM结构就能够缓解RNN中的梯度消失呢?(注意这里是缓解,并不是完美解决,LSTM层数过深时也还是有可能发生梯度消失问题)
先来回顾一下RNN导致梯度消失的原因,正是因为tanh和sigmoid函数的导数均小于1,一系列小于1的数连乘,连乘的数一多,连乘的结果就有很大概率为0,那么参数便不能进行更新了。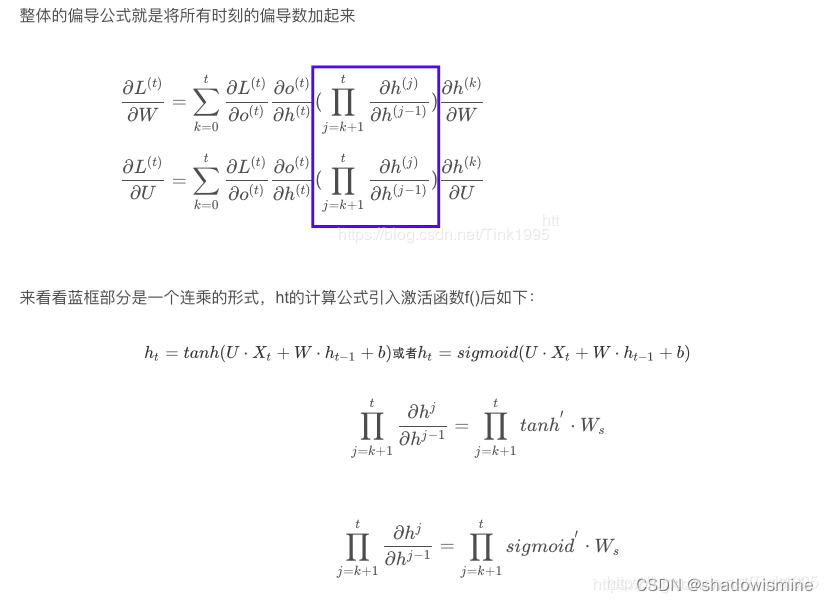
咱们类比到LSTM中:

为什么会是上述偏导连乘,其实可以通过数学公式推导,但是推导过程比较复杂,因为LSTM的参数太多了。
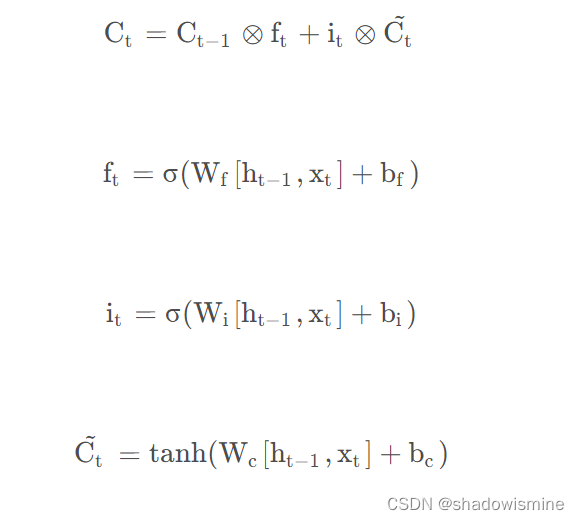
代入Ct中:
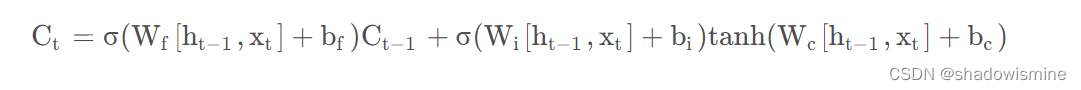
上面的公式看上去吓人,但仔细一看,后面的部分跟C{t-1}一点关系都没有,Ct对C{t-1}求偏导的话,后半边直接为0.
Ct对C{t-1}求偏导结果为:

上面的值地范围在0~1之间,但是在实际参数更新的过程中,可以通过控制bf较大,使得该值接近于1。这样即使在多次连乘的情况下,梯度也不会消失。
但是咱们回过头来再看看RNN:

虽然RNN也可以通过调整Ws来使得连乘接近于1,但是RNN是通过乘以Ws来调节,大家知道乘法数值变化较快,比较敏感,参数很难调,一不小心就超过了上界发生梯度爆炸,达不到下界不发生梯度消失。而LSTM是通过加上bf来调节,来降低梯度消失的风险,调节起来更容易,相对于RNN较好。所以之前也只是说了LSTM能相对于RNN缓解梯度消失的问题,并不能完全消除。
1.3 LSTM问题
OK,看到这,相信你对于LSTM的结构也已经有了清楚的认识。你有没有发现LSTM需要训练的参数好像有点多,Wf,Wi,Wo,Wc,bf,bi,bo,bc,V,9个参数。这是LSTM的优点也是缺点,优点是有更多的参数对于模型进行调节,结果更加精确,缺点是,参数太多了。
2. GRU(Gate Recurrent Unit)
GRU是一种也能达到LSTM相当效果,但是参数更少,相对更容易训练的算法,能够很大程度上提升训练效率,接下来咱们就来看看GRU的结构吧!
2.1 GRU结构
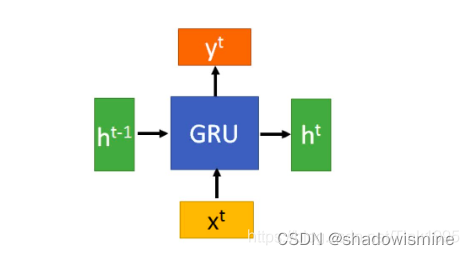
上图是GRU的整体结构图,发现跟普通的RNN没有区别,也就只有一条状态传递的通道,ht。那么接下来看看GRU中隐藏层的内部结构,到底是如何传递信息地。

上图就是GRU隐藏层的内部结构,先不要慌,虽然看上去很复杂,但是原理跟LSTM差不多,我来一步一步讲解。
LSTM有”忘记门“,”输入门“,”输出门“三个门来控制信息传递,GRU只有两个,一个是上图中的reset 重置门,一个是update 更新门。
reset 重置门:
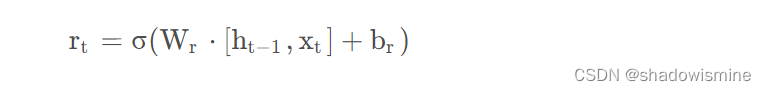
rt就是”重置门“,计算公式还是跟LSTM一样,只是处理数据的方式不同,得到”重置门“rt后,将rt与上一时刻传入的h{t-1}进行点乘,得到重置之后的数据。
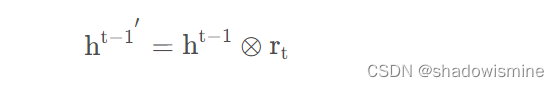
然后将得到的h{t-1}‘与Xt进行拼接。

这里的h’包含了输入信息Xt,和经过选择后的上一时刻的重要信息h{t-1}’,这样就达到了记忆当前状态信息的目的。
update 更新门:

Zt就是”更新门“,那么咱们来看看”更新门“是如何同时进行遗忘和记忆地。
先来看具体公式:


可以看到,这里的遗忘 z 和(1-z) 是联动的。也就是说,对于传递进来的维度信息,我们会进行选择性遗忘,则遗忘了多少权重 (z ),我们就会使用包含当前输入的 h’ 中所对应的权重进行弥补 (1-z) 。以保持一种”恒定“状态。
GRU只有两个门,相应地参数也就比LSTM要少,效率要高,但是结果并没有多大的区别。
原文链接:https://blog.csdn.net/Tink1995/article/details/104881633




)



)










