文章目录
- 前言
- 对20GB文件进行排序
- 超大文本中搜索两个单词的最短距离
- 从10亿数字中寻找小于100万个数字
- 总结
前言
提示:你生命的前半辈子或许属于别人,活在别人的认为里。那把后半辈子还给自己,去追随你内在的声音。 --荣格
理解了前面的几个题目知乎,这里我们在看看在海量数据场景下的查询问题。
对20GB文件进行排序
题目要求:假设你有一个20GB的文件,每行一个字符串,请说明如何对这个文件进行排序?
分析:这里给出的大小是20GB,其实面试官在暗示我们不要将所有文件都装入内存里面,因此我们只有将文件划分成块,每块大小是xMB,x就是可用的内存大小,比如如果是1GB的块,那么我们就可以将文件分成20块。我们先对每块进行排序,然后再逐步合并。这时候我们可以使用两两并归,也可以使用堆排序的策略将其逐步合并成一个,相关的可以看以往章节介绍:
这种排序方式也称为外部排序。
超大文本中搜索两个单词的最短距离
题目要求:有一个超大文本文件,内部是很多单词组成的,现在给定两个单词,请你找出这两个单词在这个文本中的最小距离。你有办法在O(n)时间里完成搜索吗?方法的空间复杂度如何。
分析:这个题目咋看起来含简单,遍历一下,找到两个单词的位置w1和w2,然后比较一下就可以了,然而这里的w1可能存在多个位置,w2也一样。看下面的图:
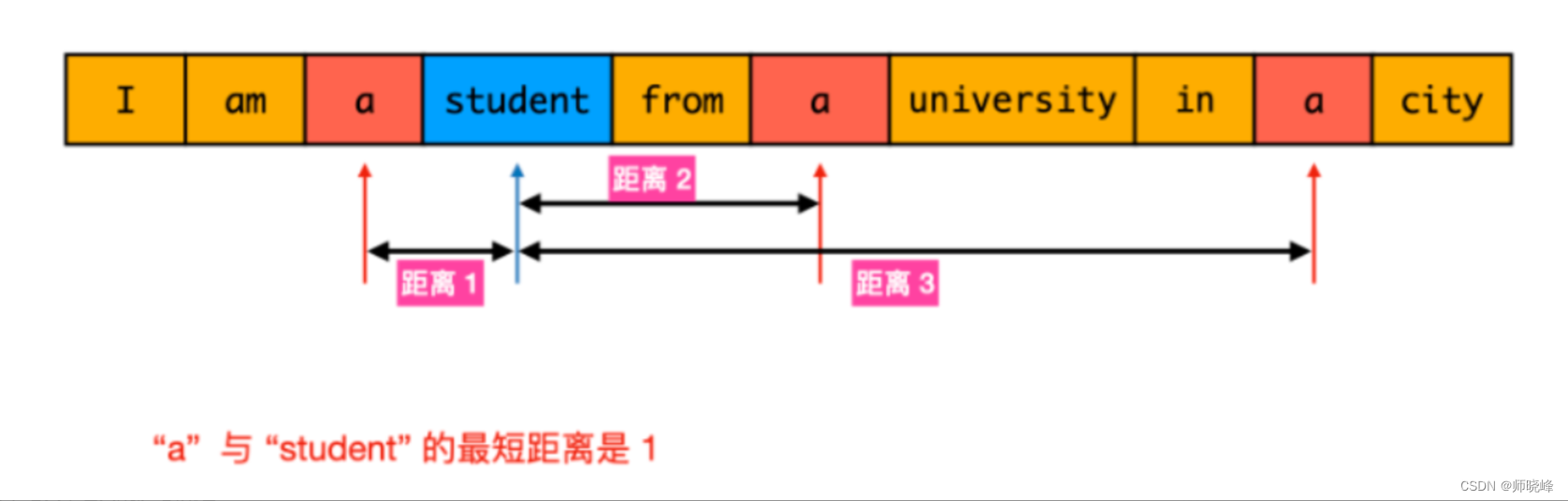
这个时候如何找到最小的距离呢?
最直观的做法就是遍历数组words,对数组中的每个word1,遍历数组words找到每个word2并计算距离。该做法的最坏的时间复杂度为O(n^2),需要优化。
本题目少不了遍历一次数组,找到所有word1和word2出现的位置,但是为了方便比较,我们可以将其放入一个数组中。比如:
ListA:{1,2,3,5,9,34}
ListB:{4,8,12,56}
合并后
List:{1a,2a,3a,4b,5b,12b,34a,56b}
合并成一个之后更方便查找的数组,数字便是出现的位置,后面的一个元素表示元素是什么,然后一遍遍历,一遍比较就可以了。
但是对于超大文本,如果文本太大那么这个list可能会产生溢出,还需要继续观察,我们或发现其实不用单独构造list,从左到右遍历数组words当遍历到word1时,如果已经遍历的单词中存在word2,为了方便记录最短距离,应该取一个已经遍历到的word2所在的下标,计算和当前下边的距离。同理,当遍历到word2时,应该取最后一个已经遍历到的word1所在的下标,计算和当前下标的距离。
经过以上分析,我们可以遍历一次数组就可以得到最短距离,并且将复杂度降低到O(n)。用index1 和index2分别表示数组word已经遍历到单词的最后一个word1和word2下标。初始状态下index1和index2为-1.遍历数组word,当遇到word2时,执行以下操作:
- 如果遇到word1,则将index1更新为当前下标;如果遇到word2,则将index2更新为当前下标。
- 如果index1和index2都非负,则计算两个下标的距离|index1 - index 2|,并用该距离更新最短距离。
遍历结束之后就可以获取word1和word2的最短距离。
进阶问题如果再寻找的过程中这个文件会重复多次,而每次寻找的单词不同,则可以维护一个哈希表记录每个短促的下标列表。遍历一次文件,按照下标递增顺序得到每个单词再文件中出现的所有下标。寻找单词时,只需要得到两个单词的下标列表。使用双指针遍历下标链表,就可以得到两个单词的最短距离
从10亿数字中寻找小于100万个数字
题目要求:设计一个算法,给定一个10亿个数字,找出最小的100万的数字。假定计算机内存足够容纳10亿个数字。
分析:本题常见的做法有三种
- 先对元素排序,然后去取出前100万个数字,该方法的时间复杂度为O(nlogn)。很明显这样做时间和空间的消耗很大
- 采用选择排序,首先遍历10亿个数找最小,然后再遍历一遍找第二小…直到找到100万个。这种方式的时间复杂度(nm),执行10亿*100万次。实现难度高
- 采用大顶堆来解决。推荐:算法通过村第十四关-堆|白银笔记|经典问题-CSDN博客 堆排序原理。
首先前提创建100万存储空间大顶堆,最大元素位于堆顶。
然后遍历整个序列,只要比堆顶元素小才可以放入堆中。并删除原堆的最大元素。之后继续遍历剩下的序列。直到最后剩下的之后100万个数字。
采用这一种遍历方式,只需要遍历一次10亿个数字,还可以接受。更新堆的代价是O(nlogn),也是勉强够用的。堆的占用空间是100万*4大约就是4MB的空间。也是不错的选择
如果数量没有这么大,上面的其他方法也不是不可以。
如果将10亿数字换成数据流,也可以采用堆的方式,而且对数据流来说,几乎能采用堆来做的。
总结
提示:超大数据排序;超大数据搜索问题;海量数据集遍历;超大规模数据流;堆的排序原理:
如果有帮助到你,请给题解点个赞和收藏,让更多的人看到 ~ ("▔□▔)/
如有不理解的地方,欢迎你在评论区给我留言,我都会逐一回复 ~
也欢迎你 关注我 ,喜欢交朋友,喜欢一起探讨问题。














)





