目录
📚词项频率及权重计算
🐇词项频率
🐇逆文档频率
🐇tf-idf权重计算
📚向量空间模型
🐇余弦相似度
🐇查询向量
🐇向量相似度计算
📚其他tf-idf权值计算方法
🐇tf的亚线性尺度变换方法
🐇基于最大值的tf归一化
🐇文档权值和查询权重机

我们需要一种方法分配一个分数,如果查询项不出现在文档,分数应该是0,更频繁的查询项的文档,分数越高。
在文档集规模很大的情况下,满足布尔查询的结果文档数量可能非常多,往往会大大超过用户能够浏览的文档数目。因此对搜索引擎来说,对文档进行评分和排序非常重要。
📚词项频率及权重计算
🐇词项频率
- 首先,我们对于词项t,根据其在文档d中的权重来计算它的得分。最简单的方式是将权重设置为t在文档中的出现次数。这种权重计算的结果称为词项频率(term frequencey),记为
,其中的两个下标分别对应词项和文档。
- 对于文档 d,利用上述 tf 权重计算方式(或者任意一个将 tf 映射成实数的权重计算函数)得到的权重集合可以看成是文档的一个经过量化以后得到的浓缩版本。
- 在这种通常称为词袋模型(bag of words model)的文档视图的情况下,词项在文档中的出现次序被忽略,但是出现的次数非常重要,这和布尔检索形成了鲜明对比。需要指出的是,这里我们只保留了词项在文档中出现的次数。
🐇逆文档频率
- 原始的词项频率会面临这样一个严重问题,即在和查询进行相关度计算时,所有的词项都被认为是同等重要的。实际上,某些词项对于相关度计算来说几乎没有或很少有区分能力。
- 例如,在一个有关汽车工业的文档集中,几乎所有的文档都会包含 auto,此时,auto就没区 分能力。为此,我们提出一种机制来降低这些出现次数过多的词项在相关性计算中的重要性。
- 一个很直接的想法就是给文档集频率(collection frequency)较高的词项赋予较低的权重,其中文档集频率指的是词项在文档集中出现的次数。这样,便可以降低具有较高文档集频率的词项的权重。
- 一个更常用到的因子是文档频率(document frequency),它表示的是出现 t 的所有文档的数目。
- 由于 df 本身往往较大,所以通常需要将它映射到一个较小的取值范围中去。为此,假定所有文档的数目为 N,词项 t 的 idf(inverse document frequency, 逆文档频率)的定义如下:
🐇tf-idf权重计算
- 对于每篇文档中的每个词项,可以将其tf和idf组合在一起形成最终的权值。如下:
- 当 t 只在少数几篇文档中多次出现时 (对应的df小,idf大), 权重取值最大 (此时能够对这些文档提供最强的 区分能力);
- 当 t 在一篇文档中出现次数很少,或者在很多文档中出现,权重取值次之(此时对最后 的相关度计算作用不大);
- 如果 t 在所有文档中都出现,那么权重取值最小。
- 这样,就可以把文档看成是一个向量(vector),其中的每个分量都对应词典中的一个词项。
- 分量值为上述公式计算出的权重值。当某词项在文档中没有出现时,其对应的分量值为 0。
- 重合度评分指标(overlap score measure),文档d的得分是所有查询词项在文档中的出现次 数 tf 之和。当然,我们可以对这种方法进行修正,即不采用 tf 而采用 tf-idf 权重求和:
📚向量空间模型
🐇余弦相似度
- 假设文档 d 对应的向量用
表示,其中每个分量对应一个词项。
- 针对两篇文档的相似度计算,考虑采用两个文档向量差向量的大小进行计算。但这种计算方式会受文档长度影响。
- 计算两篇文档相似度的常规方法是求 余弦相似度:
- 上述公式除以分母的效果实际上相当于将向量进行长度归一化(欧式归一化),得到单位向量。因此,公式可以重写为:
- 以上可以看作是两个归一化以后的文档向量的内积,也就是计算两个向量的夹角余弦。
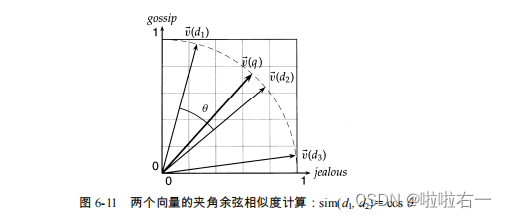
- 我们考虑在给定文档 d(也许是文档集中的某篇文档 di)的前提下在文档集中搜索与之相近的文档的过程。文档相似度计算就非常有用。
- 很自然地,将一个包含 N 篇文档的文档集看成向量的集合相当于将整个文档集看成一个 M × N 的 词项—文档矩阵 ( term-document matrix ),其中矩阵的每行代表一个词项,每列代表一篇文档。
🐇查询向量
- 将文档表示成向量的一个令人信服的理由是也可以将查询表示成向量。
- 将查询和文档看成两个向量,然后通过计算两者间的余弦相似度来衡量查询Q与文档D之间的相关性。文档或查询向量定义如下: 假设语料库中包含N个词项, 那么文档与查询向量的维数就是N,每一维度对应一个词项。
- 我们将查询看成词袋,那么就可以将查询当成一篇极短的文档来表示成向量,进而通过计算查询向量与文档向量的余弦相似度来对所有文档进行排名。这样即使一篇文档不包含所有的查询词项也可能会获得较高的余弦得分。
- 总结下来,整个检索过程就是:计算查询向量和文档集中每个文档向量的余弦相似度,结果按照得分排序,并选择得分最高的 K 篇文档。实际这个过程的代价很大,因为每次相似度计算都是数万维向量之间的内积计算,具体计算方法后续进行讨论。
🐇向量相似度计算
- 通常情况下,一个典型检索系统的配置包括:一批文档组成的文档集,其中每篇文档表示成一个向量;一个自由文本查询,也表示成一个向量;正整数 K。
- 检索系统的目标是,给定查询,从文档集合中返回得分最高的 K 篇文档。
- 向量相似度的基本算法:

📚其他tf-idf权值计算方法
🐇tf的亚线性尺度变换方法
- 即使一个词项在文档中出现了 20 次,它所携带信息的重要性也不可能是只出现1 次的词项的 20 倍。也就是说,在把一个文档复制20次之后,该文档的重要性也不应该说是比原文档大。
- 因此,可对原始的词项频率进行修改,而不仅仅是计算词项出现的次数。
- 采用原始词项频率的对数函数:
- 基于上述方式,tf就可以用wf来替代,于是就可以得到:
🐇基于最大值的tf归一化
- 采用文档中最大的词项频率对所有词项的频率进行归一化。
- 阻尼系数a是一个0到1之间的数,通常取0.4,而在一些早期的工作中使用的是 0.5。
- a 主要起平滑(smoothing)作用。
- 这里进行平滑的基本思路是当 tf 适度变化时(如从 1 变到 2 ),使用平滑技术来保证因其引起的 ntf 的波动不会非常剧烈。
- 我们发现,由于长文档中词项反复出现的可能性大,所以长文档中的词项频率倾向于取更大的值。这显然是不公平的,而 最大 tf 归一化方法的主要思路就是 减轻这种不公平所带来的影响 。
🐇文档权值和查询权重机制
- SMART系统:给不同的tf,idf实现方式命名
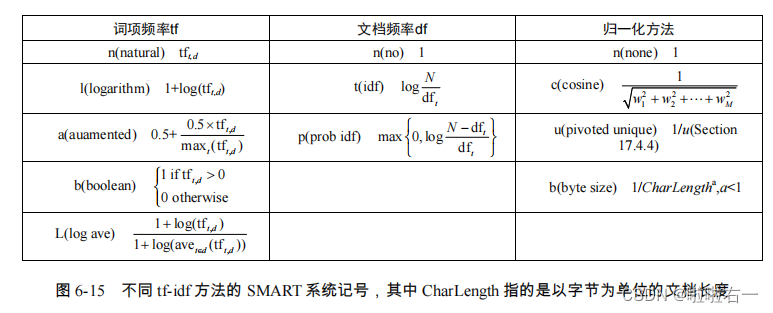
- 文档向量和查询向量权重计算方法的组合字母表示为 ddd.qqq。
- 前 3 位字母代表文档向量的权重计算方法,而后 3 位字母代表查询向量的权重计算方法。
- 每个 3 位字母组合中的第 1 位字母表示权重计算中的 tf 因子,第 2 位表示 df 因子,第 3 位表示归一化形式。
- 比如:一个普遍使用的权重计算机制是 lnc.ltc ,这表明文档向量采用了对数 tf 计算方法、没有采用 idf 因子(同时基于效 率和效果的考虑)及采用余弦归一化方法,而此时查询向量则采用了对数 tf 计算方法、 idf 权重因子 及余弦归一化方法。



)



)



)






![[传智杯 #5 初赛] I-不散的宴会](http://pic.xiahunao.cn/[传智杯 #5 初赛] I-不散的宴会)


