题目链接
文章目录
- Python3
- C++
- Morris 中序遍历 理解


Python3
方法一: 递归 ⟮ O ( n ) ⟯ \lgroup O(n) \rgroup ⟮O(n)⟯
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:"""中序遍历 [ 左子树 根 右子树 ]: 递归"""def inorder(node):if not node:return inorder(node.left) # 左子树ans.append(node.val) ## 根inorder(node.right) # 右子树ans = []inorder(root)return ans

方法二: 迭代 ⟮ O ( n ) ⟯ \lgroup O(n) \rgroup ⟮O(n)⟯
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:"""中序遍历 [ 左子树 根 右子树 ]: 迭代"""ans = []stack = []cur = rootwhile cur or stack: # 还有结点 未遍历while cur:stack.append(cur) cur = cur.left # 左 ## 开始 出栈 处理 cur = stack.pop() # ans.append(cur.val) # 根cur = cur.right # 右 return ans

方法三: Morris ⟮ O ( n ) 、 O ( 1 ) ⟯ \lgroup O(n)、O(1) \rgroup ⟮O(n)、O(1)⟯


参考链接
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:"""中序遍历 [ 左子树 根 右子树 ] Morris O(N) O(1)"""ans = []cur, pre = root, None while cur:if not cur.left:ans.append(cur.val) ## cur = cur.right # 有左孩子else:# 找 pre pre = cur.left while pre.right and pre.right != cur:pre = pre.right if not pre.right:pre.right = curcur = cur.left else:pre.right = None ans.append(cur.val)cur = cur.right return ans C++
方法一: 递归 ⟮ O ( n ) ⟯ \lgroup O(n) \rgroup ⟮O(n)⟯
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:// 子模块void inorder(TreeNode* node, vector<int> &ans){if (node == nullptr){return ;}inorder(node->left, ans);ans.emplace_back(node->val);inorder(node->right, ans);}// 主模块vector<int> inorderTraversal(TreeNode* root) {vector<int> ans;inorder(root, ans);return ans;}
};
方法二: 迭代 ⟮ O ( n ) ⟯ \lgroup O(n) \rgroup ⟮O(n)⟯
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {vector<int> ans;if (root == nullptr){return ans;}stack<TreeNode*> stk;TreeNode* cur = root;while (cur != nullptr || !stk.empty()){while (cur != nullptr){stk.emplace(cur);cur = cur->left; // 左}cur = stk.top();stk.pop();ans.emplace_back(cur->val); // 根cur = cur->right; // 右}return ans;}
};
方法三: Morris ⟮ O ( n ) 、 O ( 1 ) ⟯ \lgroup O(n)、O(1) \rgroup ⟮O(n)、O(1)⟯
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {vector<int> ans;TreeNode* cur = root;TreeNode* pre = nullptr;while (cur != nullptr){if (cur->left == nullptr){// 左子树 遍历完了ans.emplace_back(cur->val); //cur = cur->right;}else{// 找 pre pre = cur->left;while (pre->right != nullptr && pre->right != cur){pre = pre->right;}if (pre->right == nullptr){pre->right = cur;cur = cur->left;}else{pre->right = nullptr;ans.emplace_back(cur->val); //cur = cur->right; // 右}}}return ans;}
};
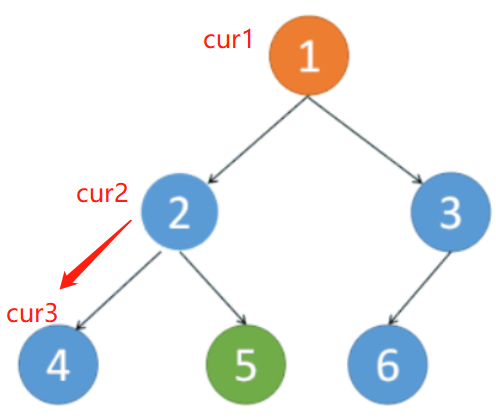
Morris 中序遍历 理解
Step 2:
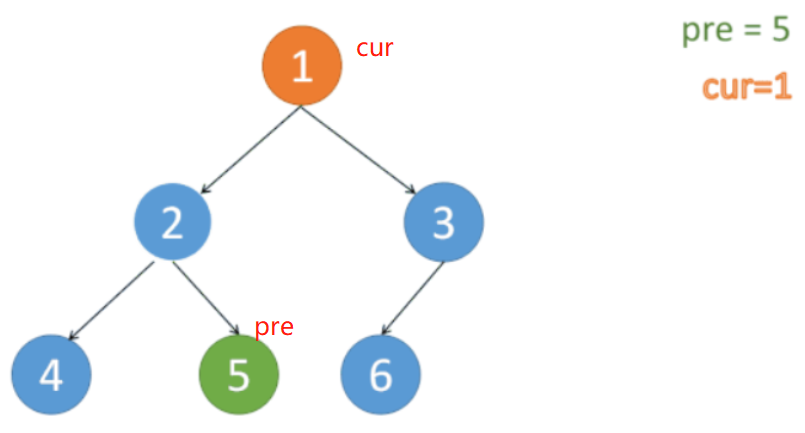
cur 移到 原树 cur 的左结点
原树:
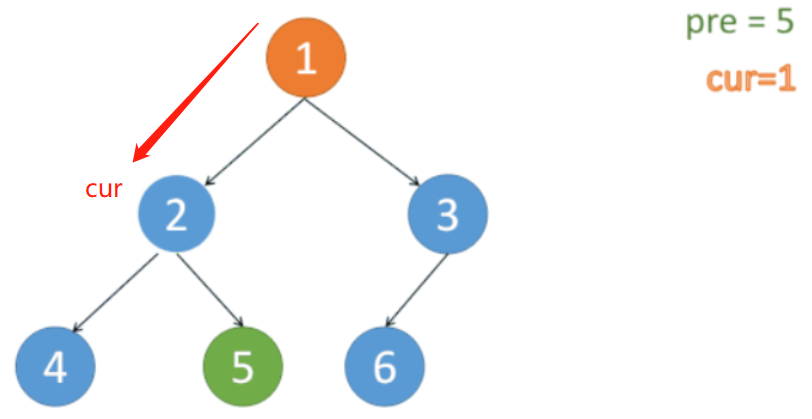
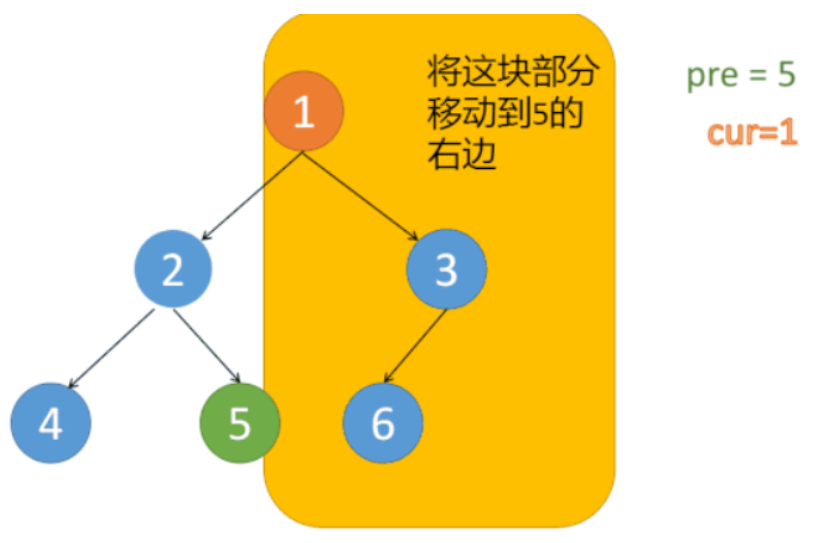
经过 step 1 操作的树
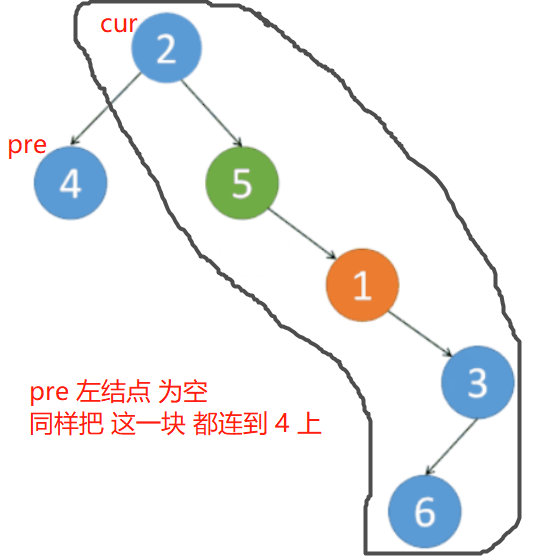
Step 3:
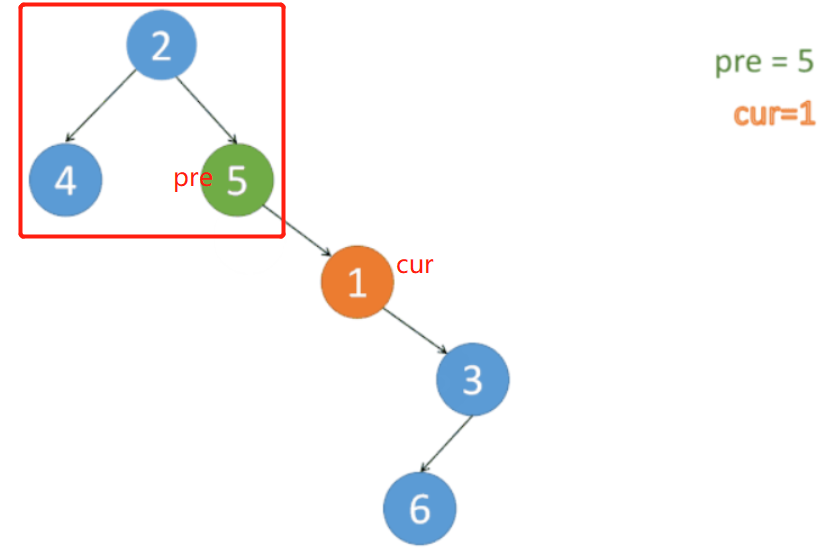
原树:
经过 step 2 操作的树
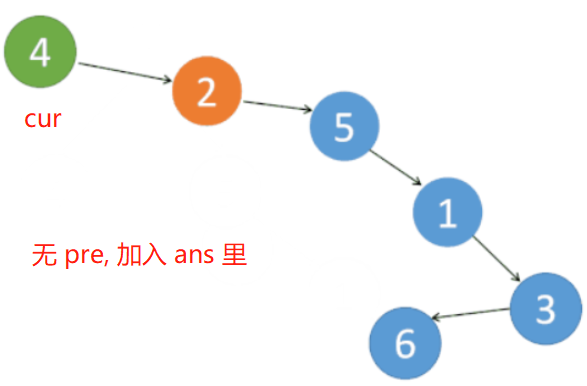
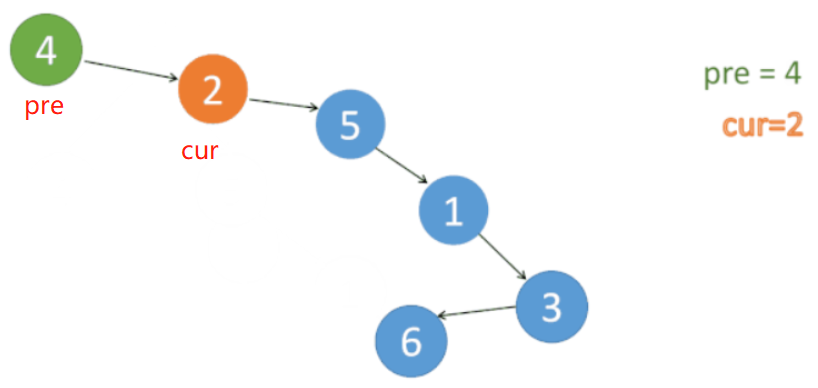
开始 有结点 加入答案里,意味着 原树最左侧的结点 遍历完成。
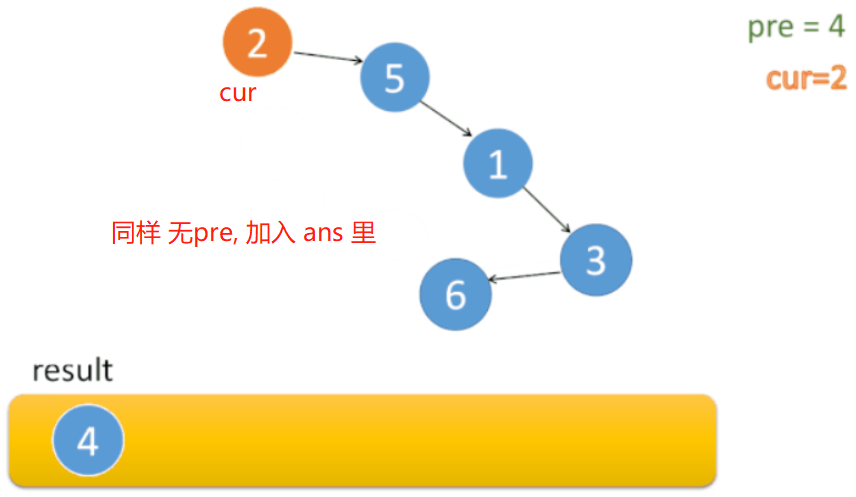
结点 4、2、5、1 依次加到 ans 里。
到 结点 3。 发现 结点 3 有 pre。
则同样 先把 cur及右子树 都加到 pre 的右边。
先处理 左边。

总体思想: 左 根 右
一般先知道 root。
把 root 及其右子树 都 接在 pre【即左子树的 mostright】 后面
处理 左子树。
这样 后面 加 答案 就是 左 根 右 的 顺序。
功能介绍)


)



 - 附代码)





)





