【面试HOT100】链表树

系列综述：
💞目的：本系列是个人整理为了秋招面试的，整理期间苛求每个知识点，平衡理解简易度与深入程度。
🥰来源：材料主要源于LeetCodeHot100进行的，每个知识点的修正和深入主要参考各平台大佬的文章，其中也可能含有少量的个人实验自证。
🤭结语：如果有帮到你的地方，就点个赞和关注一下呗，谢谢🎈🎄🌷！！！
🌈【C++】秋招&实习面经汇总篇

文章目录

      • 基本算法
      • 链表篇
        • 160. 相交链表
        • 234. 回文链表
        • 141. 环形链表
        • 142. 环形链表 II
        • 21. 合并两个有序链表
        • 19. 删除链表的倒数第 N 个结点
        • 2. 两数相加
        • 24. 两两交换链表中的节点
        • 25. K 个一组翻转链表
        • 148. 排序链表
        • 146. LRU 缓存
      • 树篇
        • 基本概述
        • 二叉树深度优先遍历
        • 二叉树广度优先遍历
        • 226. 翻转二叉树
        • 101. 对称二叉树
        • 543. 二叉树的直径
        • 108. 将有序数组转换为二叉搜索树
        • 108. 将有序数组转换为二叉搜索树
        • 98. 验证二叉搜索树
      • 树相关题目
    • 参考博客

😊点此到文末惊喜↩︎

基本算法

  1. 双指针：适合线性表
  2. 哈希法：适合去重和查找
  3. while中记录并自增，然后进行结点处理（滑动窗口模板中类似）
  4. 链表基本模板
#include <iostream>
using namespace std;// 结点模板
template<typename T>
struct Node {T data;Node *next;Node() : next(nullptr) {}Node(const T &d) : data(d), next(nullptr) {}
};// 删除 p 结点后面的元素
template<typename T>
void Remove(Node<T> *p) {// 确定两边安全性，然后删除中间if (p == nullptr || p->next == nullptr) return;auto tmp = p->next->next;delete p->next;p->next = tmp;
}//在 p 结点后面插入元素
template<typename T>
void Insert(Node<T> *p, const T &data) {auto tmp = new Node<T>(data);tmp->next = p->next;p->next = tmp;
}//遍历链表
template<typename T, typename V>
void Traverse(Node<T> *p, const V &vistor) {while(p != nullptr) {vistor(p);	// 函数指针，灵活处理p = p->next;}
}int main() {// 建立 链表结点auto p = new Node<int>(1);// 插入 链表结点Insert(p, 2);// 遍历 链表求和int sum = 0;Traverse(p, [&sum](const Node<int> *p) -> void { sum += p->data; });// 删除 链表Remove(p);return 0;
}

链表篇

160. 相交链表
  1. 问题
    • 给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。
    • 如果两个链表不存在相交节点，返回 nullptr
  2. 思路
    • 相差同移法：先求出长度差值，然后长的移动差值次，再同时移动
    • 哈希法：先将一个存入哈希表，另一个开始遍历哈希表，第一个找到另一个即为第一个。
    • 交换遍历法：pa走到头后，从headB开始走。pb走到头后，从headA开始走。这样交替走路，两个到相同结点的长度是一样的
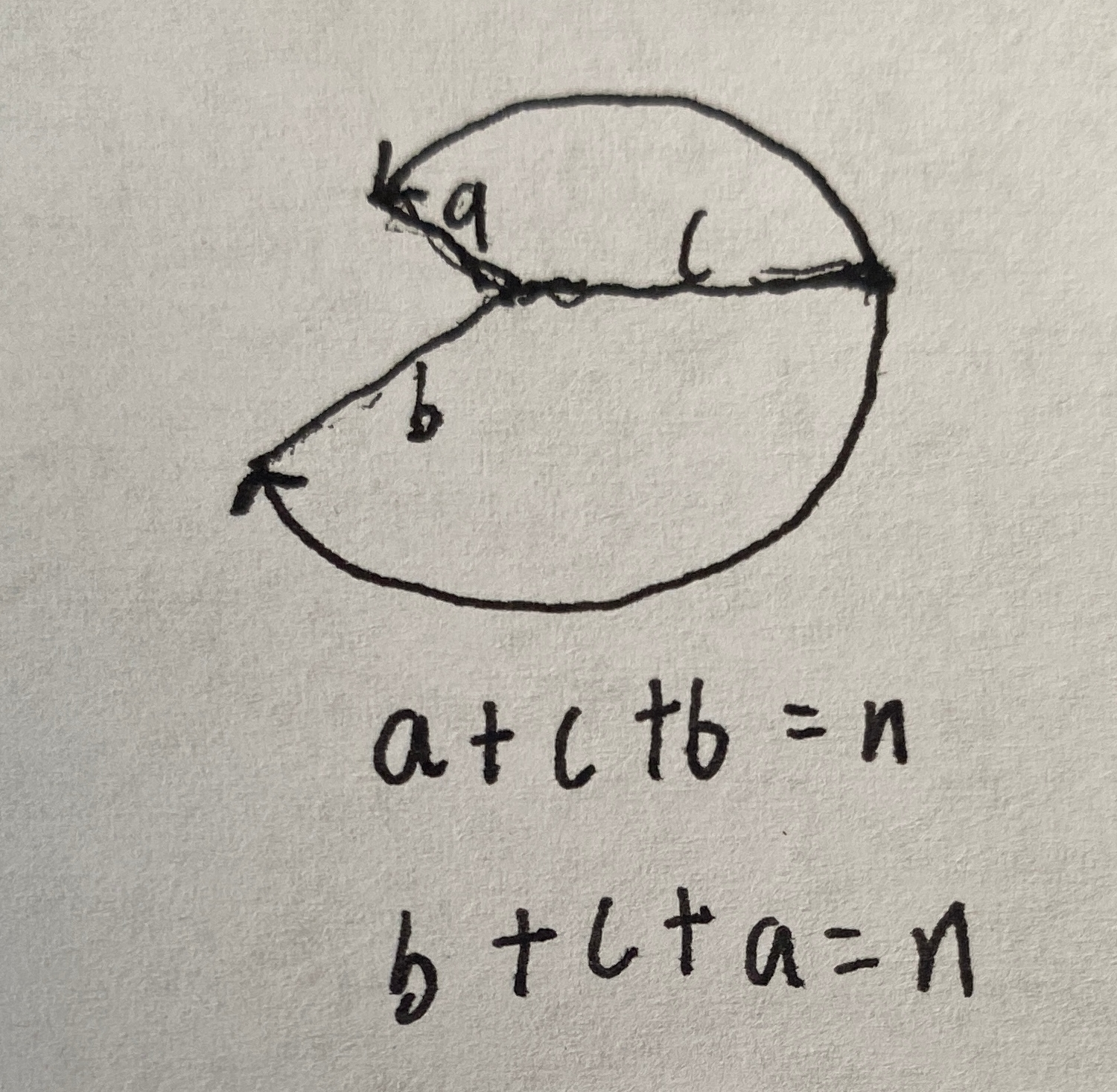
    在这里插入图片描述
// 交换遍历
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {ListNode *pa = headA;ListNode *pb = headB;while (pa != pb) {(pa == nullptr) ? pa = headB : pa = pa->next;(pb == nullptr) ? pb = headA : pb = pb->next;}return pa;
}
  1. 总结
    • 注意if-else的条件分支是否分离判断
    • 查找和去重就思考哈希
234. 回文链表
  1. 问题
    • 给你一个单链表的头节点 head ，请你判断该链表是否为回文链表。如果是，返回 true ；否则，返回 false 。最大值 。
    • 链表题目通常不能使用数组进行处理
  2. 思路
    • 链表常用模板组合
/*** Definition for singly-linked list.* public class ListNode {*     int val;*     ListNode next;*     ListNode() {}*     ListNode(int val) { this.val = val; }*     ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution {public boolean isPalindrome(ListNode head) {if(head == null || head.next == null) return true;// 找中点 1=>1 123=>2 1234=>2ListNode A_end = mid(head);ListNode B_start = A_end.next;A_end.next = null;// 翻转后半部分B_start = reverse(B_start);// 比对boolean res = compare(head, B_start);// 还原A_end.next = reverse(B_start);return res;}// 链表找中点，快慢指针法ListNode mid(ListNode head) {ListNode p = head;ListNode q = head;while(q.next != null && q.next.next != null) {p = p.next;q = q.next.next;}return p;}// 链表反转模板ListNode reverse(ListNode head) { // 三人行模板ListNode pre = null;ListNode cur = head;while(cur != null) {ListNode temp = cur.next; // 松手先保存cur.next = pre;pre = cur; // 归位cur = temp;}return pre;}// 链表比对模板(len(B) <= len(A))boolean compare(ListNode A, ListNode B) {while(B != null) {if(A.val != B.val) return false;A = A.next;B = B.next;}return true;}
}
141. 环形链表
  1. 问题
    • 给你一个链表的头节点 head ，判断链表中是否有环。
  2. 思路
    • 每次快指针移动两步，慢指针移动一步，同时移动直到快慢指针相遇即可。
// 查找：使用hash存储，然后遍历环进行处理
bool hasCycle(ListNode *head) {ListNode* fast = head;ListNode* slow = head;while (true) {if (fast == nullptr || fast->next == nullptr) return false;fast = fast->next->next;slow = slow->next;if (fast == slow) break;}return true;}
  1. 判断环的长度：快慢指针相遇后继续移动，直到第二次相遇。两次相遇间的移动次数即为环的长度
  2. 判断环的入口：快慢指针相遇后，慢指针不动，另取一指针p指向链表头结点，然后节点p和节点slow同时移动，每次移动一步，二者相遇时指向的节点即为环的入口节点。
142. 环形链表 II
  1. 问题
    • 给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。
  2. 思路
    • 判断环的入口：快慢指针相遇后，慢指针不动，另取一指针p指向链表头结点，然后节点p和节点slow同时移动，每次移动一步，二者相遇时指向的节点即为环的入口节点。
ListNode *detectCycle(ListNode *head) {ListNode* fast = head;ListNode* slow = head;while (true) {if (fast == nullptr || fast->next == nullptr) return nullptr;fast = fast->next->next;slow = slow->next;if (fast == slow) break;}fast = head;while (slow != fast) {slow = slow->next;fast = fast->next;}return fast;
}
21. 合并两个有序链表
  1. 问题
    • 将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
  2. 思路
    • 虚拟头节点的使用
ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {ListNode *vhead = new ListNode(-1, nullptr);ListNode *tail = vhead;while (list1 != nullptr && list2 != nullptr) {ListNode *p;if (list1->val < list2->val) {p = list1;list1 = list1->next;}else {p = list2;list2 = list2->next;}// 条件判断中共同的部分，分离出来tail->next = p;tail = tail->next;} list1 == nullptr ? tail->next = list2 : tail->next = list1;return vhead->next;
}
19. 删除链表的倒数第 N 个结点
  1. 问题
    • 给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。
  2. 思路
    • 虚拟头节点的使用
    • 删除结点要使用保存其前一个结点的指针
ListNode* removeNthFromEnd(ListNode* head, int n) {if(n < 0 || head == nullptr)return nullptr;// 快慢指针拉开n个节点的距离ListNode *vHead = new ListNode(0);vHead->next = head;ListNode *slow = vHead;ListNode *fast = vHead;// 让slow指向被删除节点的前一个while(n--){fast = fast->next;}// 同步移动while(fast->next != nullptr){fast = fast->next;slow = slow->next;}// 删除节点slow->next = slow->next->next;return vHead->next;
}
2. 两数相加
  1. 问题
    • 给你两个 非空 的链表，表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的，并且每个节点只能存储 一位 数字。
    • 请你将两个数相加，并以相同形式返回一个表示和的链表。
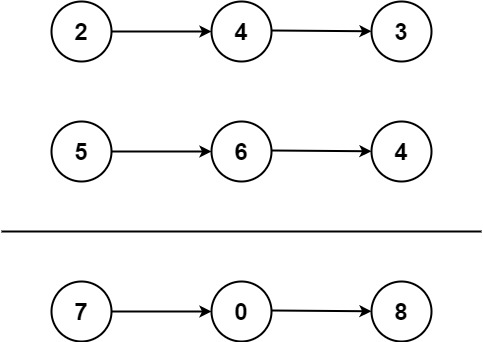
      在这里插入图片描述
  2. 思路
    • 通过进位carry和补充虚拟结点，从而实现算法的统一处理
class Solution {
public:ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {/* 定义一个新的链表用于存储求和的结果 */ListNode* dummyHead = new ListNode(0);ListNode* cur = dummyHead;/* 定义一个变量用于保存进位 */int carry = 0;/* 因为不知道l1和l2的长短所以只要有一个没有遍历完就继续遍历 遍历完的就不执行 *//* * 第一次写while(l1 || l2)会错因为漏掉了最后一个进位《== 特别哟注意*/while(l1 || l2 || carry){/* 只要不为空就继续求和 */if(l1 != NULL) carry += l1->val;if(l2 != NULL) carry += l2->val;/* 创建一个节点插入到新的链表并且值初始化为l1->val+l2->val的个位数 */ListNode* tmp = new ListNode(carry%10);/* 插入结点tmp因为是从头开始插入所以只需要每次更新cur */cur->next = tmp;cur = cur->next;/* 只要链表不为空就继续遍历下一个节点 */if(l1 != NULL) l1 = l1->next;if(l2 != NULL) l2 = l2->next;/* 获取上个节点的进位值 加到下个节点的运算中 */carry /= 10;}/* 注意这里不返回dummyHead因为这里相当于一个虚拟头节点 下一个才是正真的头节点 */return dummyHead->next;}
};
  1. 总结
    • 补充虚拟的，从而将算法进行统一化处理
24. 两两交换链表中的节点
  1. 问题
    • 给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）
  2. 思路
    • 每次确定两个结点的前一个结点，并进行交互处理
ListNode* swapPairs(ListNode* head){// 带安全检查的交换结点auto swap_list = [](ListNode *prev){if (prev != nullptr && prev->next != nullptr && prev->next->next != nullptr) {ListNode *front = prev->next;ListNode *back = front->next;front->next = back->next;back->next = front;prev->next = back;}};if(head == nullptr)return nullptr;// 单链表插/删，虚拟三件套ListNode* vHead = new ListNode(-1);vHead->next = head;					ListNode *cur = vHead;while(cur->next != nullptr && cur->next->next != nullptr){swap_list(cur);cur = cur->next->next;}return vHead->next;
}
  1. 总结
    • 使用auto匿名函数封装链表基本操作
25. K 个一组翻转链表
  1. 问题
    • 给你链表的头节点 head ，每 k 个节点一组进行翻转，请你返回修改后的链表。
  2. 算法
    • 栈：可以用来处理逆序问题
ListNode* reverseKGroup(ListNode* head, int k) {stack<ListNode*> stk;ListNode* res=new ListNode;ListNode* p=res,*q;int i;while(head){for(i=0;head&&i<k;i++){//k个一组进栈stk.push(head);head=head->next;}if(i!=k)break;//不成一组跳出while(!stk.empty()){//逆序出栈p->next=stk.top();p=stk.top();stk.pop();}q=head;}p->next=q;//接上余下的点return res->next;
}
148. 排序链表
  1. 问题
    • 给你链表的头结点 head ，请将其按 升序 排列并返回 排序后的链表
  2. 思路
    • 归并
ListNode* sortList(ListNode* head) {ListNode dummyHead(0);dummyHead.next = head;auto p = head;int length = 0;while (p) {++length;p = p->next;}for (int size = 1; size < length; size <<= 1) {auto cur = dummyHead.next;auto tail = &dummyHead;while (cur) {auto left = cur;auto right = cut(left, size); // left->@->@ right->@->@->@...cur = cut(right, size); // left->@->@ right->@->@  cur->@->...tail->next = merge(left, right);while (tail->next) {tail = tail->next;}}}return dummyHead.next;
}
// 分离链表
ListNode* cut(ListNode* head, int n) {// p指向链表的第n个auto p = head;while (--n && p) {p = p->next;}if (p == nullptr) return nullptr;// 返回链表后的结点，并将该段链表分离auto next = p->next;p->next = nullptr;return next;
}
// 合并两个有序链表
ListNode* merge(ListNode* l1, ListNode* l2) {ListNode dummyHead(0);auto p = &dummyHead;while (l1 && l2) {if (l1->val < l2->val) {p->next = l1;p = l1;l1 = l1->next;       } else {p->next = l2;p = l2;l2 = l2->next;}}p->next = (l1 ? l1 : l2);return dummyHead.next;
}
146. LRU 缓存

树篇

基本概述
  1. 二叉树数据结构
    struct TreeNode {int val;TreeNode *left;TreeNode *right;TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
二叉树深度优先遍历
  1. 递归式
    // 前序遍历
void Traversal(TreeNode *root) {if (root == nullptr) return ;Doing(root->val);       // 中Traversal(root->left);  // 左Traversal(root->right); // 右
}
// 中序遍历
void Traversal(TreeNode *root) {if (root == nullptr) return ;Traversal(root->left);  // 左Doing(root->val);       // 中Traversal(root->right); // 右
}
// 后序遍历
void Traversal(TreeNode *root, vector<int> vec) {if (root == nullptr) return ;Traversal(root->left);  // 左Traversal(root->right); // 右vec.emplace_back(root->val);// 中
}
  2. 非递归：将前序、中序和后序统一化处理，将遍历核心顺序进行逆序转化
    • 算法遍历部分的逆序
    • 对于值节点的处理
    vector<int> Traversal(TreeNode* root) {// 初始化vector<int> result;		// 结果容器stack<TreeNode*> st;	// 深度的栈if (root != NULL) 		// 根非空则入栈st.push(root);// 遍历源容器while (!st.empty()) {TreeNode* node = st.top();	//   if (node != NULL) {st.pop();// 算法变化的部分，遍历的逆序// 中st.push(node);                          st.push(NULL);// 右if (node->right) st.push(node->right); // 左if (node->left) st.push(node->left);    } else {// 对值节点的处理st.pop();// 弹出空值结点node = st.top();st.pop();// 结点处理result.push_back(node->val);}}return result;
}
二叉树广度优先遍历
  1. 递归法
    // 递归参数，如果需要修改要进行引用传递
void traversal(TreeNode* cur, vector<vector<int>>& result, int depth) {// 递归出口if (cur == nullptr) return;// 递归体if (result.size() == depth) // 扩容result.push_back(vector<int>());// 原地构建数组result[depth].push_back(cur->val);// 顺序压入对应深度的数组中order(cur->left, result, depth + 1);order(cur->right, result, depth + 1);
}
vector<vector<int>> levelOrder(TreeNode* root) {// 初始化：一般为递归形参vector<vector<int>> result;int depth = 0;// 递归调用traversal(root, result, depth);// 返回结果return result;
}
  2. 非递归法
vector<vector<int>> levelOrder(TreeNode* root) {// 初始化vector<vector<int>> result;	// 结果容器queue<TreeNode*> que;		// 广度的队列if(root != nullptr)			// 根非空则入列 que.push(root);// 算法while (!que.empty()) {		// 队列非空vector<int> vec;		// 结果存放TreeNode* node; 		// 过程记录int size = que.size();	// 初始化：记录每层要遍历的根节点数量for (int i = 0; i < size; i++) {	// que.size()会变化// 处理结点node = que.front();	// 记录队首结点que.pop();			// 弹出队首结点if (node->left) que.push(node->left);if (node->right) que.push(node->right);// doing：处理结点vec.push_back(node->val);}// 将每层筛选元素压入结果数组中result.push_back(vec);}// 输出return result;
}
226. 翻转二叉树
  1. 给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。
  2. 思路
    • 前序遍历
void traversal(TreeNode *cur){// 结束条件if(cur == nullptr)return ;swap(cur->left, cur->right);if(cur->left)  traversal(cur->left);if(cur->right)  traversal(cur->right);
}
101. 对称二叉树
  1. 给你一个二叉树的根节点 root ， 检查它是否轴对称。
  2. 思路
    • 单层条件尝试
bool ismirror(TreeNode* t1,TreeNode* t2){if(t1==NULL&&t2==NULL)//都为空return true;if(t1==NULL||t2==NULL)//有一个为空return false;return (t1->val==t2->val)&&ismirror(t1->left,t2->right)&&ismirror(t1->right,t2->left);
}
543. 二叉树的直径
  1. 问题
    • 给你一棵二叉树的根节点，返回该树的 直径 。
    • 二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。
  2. 思路
    • 最长一定是以某个结点为根节点的子树的左右子树高度之和
int diameterOfBinaryTree(TreeNode* root)
{int distance = 0;dfs(root, distance);return distance;
}// distance等价于全局变量
int dfs(TreeNode *root, int &distance){if (root == nullptr)return 0;int left = dfs(root->left, distance);	// 左边深度int right = dfs(root->right, distance);	// 右边深度distance = max(left + right, distance);	// // 获取当前树的左子树和右子树深度的较大值，加 1 （本层深度）return max(left, right) + 1;	// 最大深度
}
108. 将有序数组转换为二叉搜索树
  1. 问题
    • 给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 高度平衡 二叉搜索树。
    • 高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。
  2. 思路
    • 建根和划分
TreeNode* Translate(vector<int>& nums, int left, int right) {if (left > right) return nullptr;// 建根int mid = left + ((right - left) / 2);TreeNode *root = new TreeNode(nums[mid]);// 划分root->left = Translate(nums, left, mid-1);root->right = Translate(nums, mid+1, right);// 返回return root;
}
108. 将有序数组转换为二叉搜索树
  1. 问题
    • 给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 高度平衡 二叉搜索树。
    • 高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。
  2. 思路
    • 建根和划分
TreeNode* Translate(vector<int>& nums, int left, int right) {if (left > right) return nullptr;// 建根int mid = left + ((right - left) / 2);TreeNode *root = new TreeNode(nums[mid]);// 划分root->left = Translate(nums, left, mid-1);root->right = Translate(nums, mid+1, right);// 返回return root;
}
98. 验证二叉搜索树
  1. 问题
    • 给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。对值不超过 1 的二叉树。
  2. 思路
    • 二叉树的中序遍历是递增顺序的
    • 判断左小右大
// 中序递增
long pre = MIN_                                                                                                                                                                                                                       ;
public boolean isValidBST(TreeNode root) {if (root == null) {return true;}// 访问左子树if (!isValidBST(root.left)) {return false;}// 访问当前节点：如果当前节点小于等于中序遍历的前一个节点，说明不满足BST，返回 false；否则继续遍历。if (root.val <= pre) {	// 严格递增return false;}pre = root.val;// 访问右子树return isValidBST(root.right);
}

树相关题目

少年，我观你骨骼清奇，颖悟绝伦，必成人中龙凤。
不如点赞·收藏·关注一波

🚩点此跳转到首行↩︎

参考博客

  1. 前缀和问题
  2. 单调队列
  3. 快速链表quicklist
  4. 《深入理解计算机系统》
  5. 侯捷C++全系列视频
  6. 待定引用
  7. 待定引用
  8. 待定引用

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/113780.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

python自动化测试框架unittest与pytest的区别

python自动化测试框架unittest与pytest的区别

有使用过unittest单元测试框架&#xff0c;再使用pytest单元测试框架&#xff0c;就可以明显感觉到pytest比unittest真的简洁、方便很多。 unittest与pytest的区别&#xff1a; 主要从用例编写规则、用例的前置和后置、参数化、断言、用例执行、失败重运行和报告这几个方面比…
阅读更多...
vue使用pdf 导出当前页面，（jspdf， html2canvas ）

vue使用pdf 导出当前页面，（jspdf， html2canvas ）

需要安装两个插件 npm install html2canvas jspdfyarn add html2canvas jspdf<div class"app-container" id"pdfPage"><!--这个放你需要导出的内容--> </div><el-button size"mini" click"onExportPdf">导出…
阅读更多...
记录一次线下渗透电气照明系统(分析与实战)

记录一次线下渗透电气照明系统(分析与实战)

项目地址:https://github.com/MartinxMax/S-Clustr 注意 本次行动未造成任何设备损坏,并在道德允许范围内测试 >ethical hacking< 发现过程 在路途中,发现一个未锁的配电柜,身为一个电工自然免不了好奇心(非专业人士请勿模仿,操作不当的话220V人就直了) 根据照片,简…
阅读更多...
springBoot--web--http缓存机制测试

springBoot--web--http缓存机制测试

springBoot--web--http缓存机制测试 前言1、多端内容适配基于请求头内容协商&#xff08;默认开启&#xff09;基于请求参数内容协商&#xff08;需要开启&#xff09; 2、默认返回json数据3、设置返回xml数据导入jackson-dataformat-xml包在类文件中添加注解 JacksonXmlRootEl…
阅读更多...
设计模式截图记录

设计模式截图记录

设计模式截图记录
阅读更多...
普通二维码跳转微信小程序实战

普通二维码跳转微信小程序实战

简介 服务端springboot项目,前端基于uniapp的微信小程序,要求扫描二维码之后进入到小程序指定页面,下面记录一下实现过程以及过程中遇到的问题. 实现过程 下面是成功跳转的配置截图: 首先说下二维码规则,这个地方需要填写扫描二维码之后打开的地址,这个地址在我的项目里…
阅读更多...
idea热加载，JRebel 插件是目前最好用的热加载插件，它支持 IDEA Ultimate 旗舰版、Community 社区版

idea热加载，JRebel 插件是目前最好用的热加载插件，它支持 IDEA Ultimate 旗舰版、Community 社区版

1.如何安装 ① 点击 https://plugins.jetbrains.com/plugin/4441-jrebel-and-xrebel/versions 地址&#xff0c;下载 2022.4.1 版本。如下图所示&#xff1a; ② 打开 [Preference -> Plugins] 菜单&#xff0c;点击「Install Plugin from Disk…」按钮&#xff0c;选择刚下…
阅读更多...
腾讯云创建了jenkins容器，但无法访问

腾讯云创建了jenkins容器，但无法访问

1、首先&#xff0c;查看本机能不能ping通你的腾讯云服务器 如果ping的通那就下一步 2、查看腾讯云服务器的防火墙关了没&#xff0c;没关关掉、 firewall-cmd --state not running 3、那就在云服务器的控制台开放端口
阅读更多...
Linux：程序地址空间/虚拟地址等相关概念理解

Linux：程序地址空间/虚拟地址等相关概念理解

文章目录 程序地址空间虚拟地址和物理地址地址的转换地址空间是什么&#xff1f; 程序地址空间 在C和C程序中&#xff0c;一直有一个观点是&#xff0c;程序中的各个变量等都会有一定的地址空间&#xff0c;因此才会有诸如取地址&#xff0c;通过地址访问等操作&#xff0c;那…
阅读更多...
线性代数-Python-02：矩阵的基本运算 - 手写Matrix及numpy中的用法

线性代数-Python-02：矩阵的基本运算 - 手写Matrix及numpy中的用法

文章目录 一、代码仓库二、矩阵的基本运算2.1 矩阵的加法2.2 矩阵的数量乘法2.3 矩阵和向量的乘法2.4 矩阵和矩阵的乘法2.5 矩阵的转置 三、手写Matrix代码Matrix.pymain_matrix.pymain_numpy_matrix.py 一、代码仓库 https://github.com/Chufeng-Jiang/Python-Linear-Algebra-…
阅读更多...
Golang笔记

Golang笔记

01 = 和 := 的区别？ 前者是赋值变量，后者是定义变量 02 指针的作用 指针指向变量的地址，在64位机器上占8个字节 【1 字节（Byte）= 8 位（bit） 1 千字节（KB，Kilobyte）= 1,024 字节（2^10 字节）】 作用 取址然后取值swap函数 交换变量的值指针接收器来改变结构体里面…
阅读更多...
Python机器学习入门指南

Python机器学习入门指南

前言 机器学习 作为人工智能领域的核心组成&#xff0c;是计算机程序学习数据经验以优化自身算法&#xff0c;并产生相应的“智能化的”建议与决策的过程。 一个经典的机器学习的定义是&#xff1a; A computer program is said to learn from experience E with respect to …
阅读更多...
打造属于自己的vue图标库

打造属于自己的vue图标库

hfex-icon图标库 Install npm i -D hfex-icon主要提供2种使用方式 方式一 通过svg图标资源&#xff0c;借助unplugin-icons库将svg图标文件生成vue组件&#xff0c;然后通过vue组件的引入方式在vue中使用 unplugin-icons 兼容vue2和vue3 在vue.config.js的plugins中配置…
阅读更多...
【C语言】进阶——程序编译

【C语言】进阶——程序编译

目录 一&#xff1a;&#x1f512;程序环境 程序的翻译环境和执行环境 &#x1f4a1;1.1翻译环境 预编译阶段&#xff1a; 编译阶段&#xff1a; 汇编阶段&#xff1a; 链接阶段&#xff1a; &#x1f4a1;1.2运行环境 二&#xff1a;&#x1f512;预处理详解 &…
阅读更多...
文件夹图片相似图片检测并删除相似图片

文件夹图片相似图片检测并删除相似图片

项目开源地址 pip install imagededupgit clone https://github.com/idealo/imagededup.git cd imagededup pip install "cython>0.29" python setup.py installQuick Start from imagededup.methods import PHash phasher PHash()# Generate encodings for all…
阅读更多...
分类预测 | Matlab实现WOA-BiLSTM鲸鱼算法优化双向长短期记忆神经网络的数据多输入分类预测

分类预测 | Matlab实现WOA-BiLSTM鲸鱼算法优化双向长短期记忆神经网络的数据多输入分类预测

分类预测 | Matlab实现WOA-BiLSTM鲸鱼算法优化双向长短期记忆神经网络的数据多输入分类预测 目录 分类预测 | Matlab实现WOA-BiLSTM鲸鱼算法优化双向长短期记忆神经网络的数据多输入分类预测分类效果基本描述程序设计参考资料 分类效果 基本描述 1.Matlab实现WOA-BiLSTM鲸鱼算法…
阅读更多...
oracle-AWR报告生成方法

oracle-AWR报告生成方法

AWR报告生成方法 1. 以oracle用户登陆服务器 2. 进入到要保存awr报告的目录 3. 以sysdba身份连接数据库 sqlplus / as sysdba4. 执行生成AWR报告命令 ?/rdbms/admin/awrrpt.sql5. 选择AWR报告的文件格式 6. 选择生成多少天的AWR报告 7. 选择报告的快照起始和结束ID 8. 输入生…
阅读更多...
MongoDB深度学习

MongoDB深度学习

MongoDB的简介 什么是MongoDB? MongoDB是一个基于分布式文件存储的数据库&#xff0c;由C语言编写。MongoDB是一个介于关系数据库和非关系数据库之间的产品&#xff0c;是非关系数据库当中功能最丰富&#xff0c;最像关系数据库的&#xff0c;它支持的数据结构非常松散&…
阅读更多...
面试算法31：最近最少使用缓存

面试算法31：最近最少使用缓存

题目 请设计实现一个最近最少使用&#xff08;Least Recently Used&#xff0c;LRU&#xff09;缓存&#xff0c;要求如下两个操作的时间复杂度都是O&#xff08;1&#xff09;。 get&#xff08;key&#xff09;&#xff1a;如果缓存中存在键key&#xff0c;则返回它对应的值…
阅读更多...
【二维差分】ICPC南京 A

【二维差分】ICPC南京 A

https://codeforces.com/gym/104128/problem/A 题意 思路 二维差分经典模型 考虑如果没有洞那么经历操作之后会剩下什么样子的袋鼠。发现上下左右移动可以看成是边界在移动&#xff0c;边界一直保持一个原初的矩形形状&#xff0c;而且上下移动和左右移动没有任何关系。一旦…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023