R语言：因子分析 factor analysis

文章目录

        • 因子分析
        • 数据集
        • 处理步骤
        • 主成分法做因子分析
        • 最大似然法做因子分析

因子分析

  • 因子分析的用途与主成分分析类似，它也是一种降维方法。由于因子往往比主成分更易得到解释，故因子分析比主成分分析更容易成功，从而有更广泛的应用。

  • 从方法上来说，因子分析比主成分分析更为精细，自然理论上也就更为复杂。主成分分析只涉及一般的线性变换，不涉及模型，仅需假定二阶矩存在。而因子分析需建立一个数学模型，并作一定的假定。

  • 因子分析起源于20世纪初，K.皮尔逊(Pearson)和C.斯皮尔曼(Spearman)等学者为定义和测定智力所作的努力，主要是由对心理测量学有兴趣的科学家们培育和发展了因子分析。

  • 因子分析的目的是为了降维，降维的方式是试图用少数几个潜在的、不可观测的随机变量来描述原始变量间的协方差关系。

数据集

内置的mtcars数据框包含有关32辆汽车的信息，包括它们的重量，燃油效率（以每加仑英里为单位），速度等。

数据来自1974年美国汽车趋势杂志，包括32辆汽车（1973-74款）的油耗和10个方面的汽车设计和性能。

> help("mtcars")Motor Trend Car Road Tests
Description
The data was extracted from the 1974 Motor Trend US magazine, and comprises fuel consumption and 10 aspects of automobile design and performance for 32 automobiles (1973–74 models).Usage
mtcars
Format
A data frame with 32 observations on 11 (numeric) variables.[, 1]	mpg	Miles/(US) gallon
[, 2]	cyl	Number of cylinders
[, 3]	disp	Displacement (cu.in.)
[, 4]	hp	Gross horsepower
[, 5]	drat	Rear axle ratio
[, 6]	wt	Weight (1000 lbs)
[, 7]	qsec	1/4 mile time
[, 8]	vs	Engine (0 = V-shaped, 1 = straight)
[, 9]	am	Transmission (0 = automatic, 1 = manual)
[,10]	gear	Number of forward gears
[,11]	carb	Number of carburetors
Source
Henderson and Velleman (1981), Building multiple regression models interactively. Biometrics, 37, 391–411.Examples
require(graphics)
pairs(mtcars, main = "mtcars data", gap = 1/4)
coplot(mpg ~ disp | as.factor(cyl), data = mtcars,panel = panel.smooth, rows = 1)
## possibly more meaningful, e.g., for summary() or bivariate plots:
mtcars2 <- within(mtcars, {vs <- factor(vs, labels = c("V", "S"))am <- factor(am, labels = c("automatic", "manual"))cyl  <- ordered(cyl)gear <- ordered(gear)carb <- ordered(carb)
})
summary(mtcars2)
处理步骤
  1. 根据研究的问题选取原始变量
  2. 对原始变量进行标准化并求出相关阵，分析变量之间的相关性
  3. 求解初始公因子及其因子载荷矩阵
  4. 因子旋转
  5. 计算因子得分
  6. 绘制因子载荷图，因子得分图
主成分法做因子分析
  • 不做因子旋转，使用原始数据
    因子数选择为3个
library("psych")fac<-principal(mtcars,3,rotate="none")
fac
  • 不做因子旋转，使用相关系数矩阵
    有些题目直接给出相关系数矩阵，没有原始数据，也可以使用因子分析的主成分法，得到的结果相同

Standardized loadings：标准化后的载荷矩阵

Principal Components Analysis
Call: principal(r = R, nfactors = 3, rotate = "none")
Standardized loadings (pattern matrix) based upon correlation matrixPC1   PC2   PC3   h2    u2 com
mpg  -0.93  0.03 -0.18 0.90 0.099 1.1
cyl   0.96  0.07 -0.14 0.95 0.052 1.1
disp  0.95 -0.08 -0.05 0.90 0.095 1.0
hp    0.85  0.41  0.11 0.90 0.104 1.5
drat -0.76  0.45  0.13 0.79 0.212 1.7
wt    0.89 -0.23  0.27 0.92 0.081 1.3
qsec -0.52 -0.75  0.32 0.94 0.063 2.2
vs   -0.79 -0.38  0.34 0.88 0.122 1.8
am   -0.60  0.70 -0.16 0.88 0.120 2.1
gear -0.53  0.75  0.23 0.90 0.098 2.0
carb  0.55  0.67  0.42 0.93 0.069 2.6PC1  PC2  PC3
SS loadings           6.61 2.65 0.63
Proportion Var        0.60 0.24 0.06
Cumulative Var        0.60 0.84 0.90
Proportion Explained  0.67 0.27 0.06
Cumulative Proportion 0.67 0.94 1.00Mean item complexity =  1.7
Test of the hypothesis that 3 components are sufficient.The root mean square of the residuals (RMSR) is  0.03 Fit based upon off diagonal values = 1

从累积方差贡献率来看，取3个因子的累积方差贡献率为90%，取两个因子的累积方差贡献率为84%。
因此我们可以将因子数减少到两个，有利于可视化分析。

fac<-principal(mtcars,2,rotate="none")
facPrincipal Components Analysis
Call: principal(r = mtcars, nfactors = 2, rotate = "none")
Standardized loadings (pattern matrix) based upon correlation matrixPC1   PC2   h2    u2 com
mpg  -0.93  0.03 0.87 0.131 1.0
cyl   0.96  0.07 0.93 0.071 1.0
disp  0.95 -0.08 0.90 0.098 1.0
hp    0.85  0.41 0.88 0.116 1.4
drat -0.76  0.45 0.77 0.228 1.6
wt    0.89 -0.23 0.85 0.154 1.1
qsec -0.52 -0.75 0.83 0.165 1.8
vs   -0.79 -0.38 0.76 0.237 1.4
am   -0.60  0.70 0.85 0.146 2.0
gear -0.53  0.75 0.85 0.150 1.8
carb  0.55  0.67 0.76 0.244 1.9PC1  PC2
SS loadings           6.61 2.65
Proportion Var        0.60 0.24
Cumulative Var        0.60 0.84
Proportion Explained  0.71 0.29
Cumulative Proportion 0.71 1.00Mean item complexity =  1.5
Test of the hypothesis that 2 components are sufficient.The root mean square of the residuals (RMSR) is  0.05 with the empirical chi square  9.45  with prob <  1 Fit based upon off diagonal values = 0.99

可以发现，因子数从3个减少到2个时，使用主成分法，前两个主成分的方差贡献率不会变化。这跟最大似然法不同。

  • 绘制因子载荷图
#绘制因子载荷图
plot(fac1$loadings,xlab="Factor1",ylab="Factor2")
abline(h=0);abline(v=0)

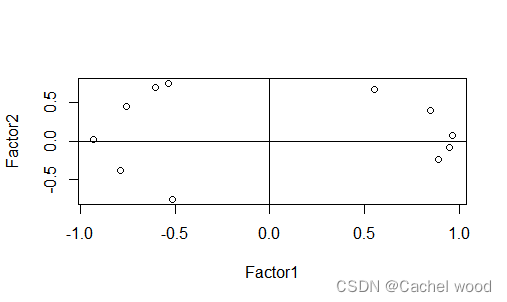
在这里插入图片描述
可以发现很多点离两个因子都比较远，不好解释。

  • 主成分法，使用最大方差法进行因子旋转
    因子数选择为2，并计算因子得分
> #主成分法,方差最大化做因子正交旋转
> fac2<-principal(mtcars,2,rotate="varimax")
> fac2
Principal Components Analysis
Call: principal(r = mtcars, nfactors = 2, rotate = "varimax")
Standardized loadings (pattern matrix) based upon correlation matrixRC1   RC2   h2    u2 com
mpg   0.68 -0.63 0.87 0.131 2.0
cyl  -0.64  0.72 0.93 0.071 2.0
disp -0.73  0.60 0.90 0.098 1.9
hp   -0.32  0.88 0.88 0.116 1.3
drat  0.85 -0.21 0.77 0.228 1.1
wt   -0.80  0.46 0.85 0.154 1.6
qsec -0.16 -0.90 0.83 0.165 1.1
vs    0.30 -0.82 0.76 0.237 1.3
am    0.92  0.08 0.85 0.146 1.0
gear  0.91  0.17 0.85 0.150 1.1
carb  0.08  0.87 0.76 0.244 1.0RC1  RC2
SS loadings           4.67 4.59
Proportion Var        0.42 0.42
Cumulative Var        0.42 0.84
Proportion Explained  0.50 0.50
Cumulative Proportion 0.50 1.00Mean item complexity =  1.4
Test of the hypothesis that 2 components are sufficient.The root mean square of the residuals (RMSR) is  0.05 with the empirical chi square  9.45  with prob <  1 Fit based upon off diagonal values = 0.99> #计算因子得分
> fac2$scoresRC1        RC2
Mazda RX4            0.913545261  0.5740734
Mazda RX4 Wag        0.827547997  0.5013891
Datsun 710           0.698816380 -0.8074274
Hornet 4 Drive      -0.913638812 -1.1047271
Hornet Sportabout   -0.859350144  0.2025926
Valiant             -1.162422544 -1.2190911
Duster 360          -0.680268641  0.9486423
Merc 240D           -0.056857408 -1.1835017
Merc 230            -0.212468151 -1.4696568
Merc 280             0.075581300 -0.2109478
Merc 280C            0.002444315 -0.2763119
Merc 450SE          -0.904174186  0.3064233
Merc 450SL          -0.849329738  0.2529898
Merc 450SLC         -0.927001103  0.2287337
Cadillac Fleetwood  -1.417403948  0.6862707
Lincoln Continental -1.392296773  0.7416873
Chrysler Imperial   -1.161445427  0.7799435
Fiat 128             0.930026590 -1.1606987
Honda Civic          1.455372982 -0.8414166
Toyota Corolla       1.040852468 -1.2543364
Toyota Corona       -0.374988630 -1.4259630
Dodge Challenger    -1.026764303  0.1466255
AMC Javelin         -0.893224853  0.1071275
Camaro Z28          -0.502907752  1.0677154
Pontiac Firebird    -0.984122353  0.2236560
Fiat X1-9            0.926969145 -1.0092451
Porsche 914-2        1.590766193  0.1745827
Lotus Europa         1.509486177 -0.3106522
Ford Pantera L       1.103849172  1.8802235
Ferrari Dino         1.361140948  1.3909629
Maserati Bora        1.120968759  2.6074298
Volvo 142E           0.761297080 -0.5470932
>

因子旋转之后，每个变量在某个因子上的载荷接近正负1，而在另一个因子上的载荷接近0，有助于我们进行解释分析。

  • 绘制新的因子载荷图
#绘制因子载荷图
plot(fac2$loadings,xlab="Factor1",ylab="Factor2")
abline(h=0);abline(v=0)

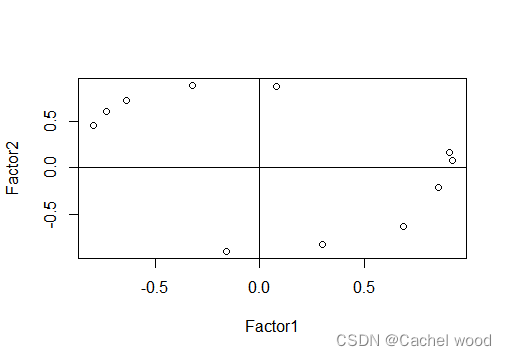
在这里插入图片描述

  • 绘制因子得分图
#绘制每个学生的因子得分图与原坐标在因子上的方向，反应因子与原始数据的关系
biplot(fac2$scores,fac2$loadings)

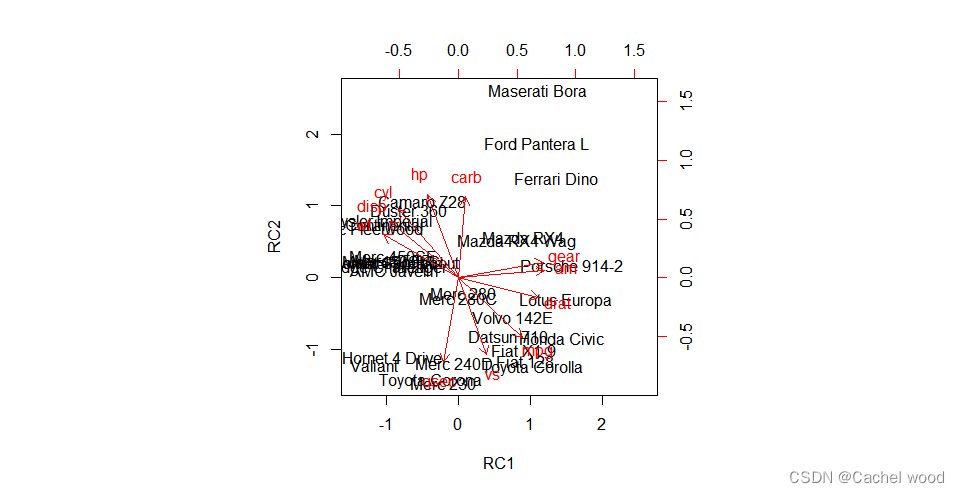
在这里插入图片描述

  • 主成分法分析
因子数有无因子旋转因子1方差贡献率因子2方差贡献率两因子累积贡献率
因子数为2无因子旋转60%24%84%
因子数为2有因子旋转42%42%84%
因子数为3无因子旋转60%24%84%
因子数为3有因子旋转41%29%70%

结论1：进行因子旋转会改变各因子的方差贡献率，但不会改变总方差贡献率
结论2：因子数不同，不进行因子旋转时，因子的方差贡献率不变

最大似然法做因子分析
  • 不做因子旋转
#用极大似然法做因子分析
factanal(mtcars,factors = 2,rotation = "none")Call:
factanal(x = mtcars, factors = 2, rotation = "none")Uniquenesses:mpg   cyl  disp    hp  drat    wt  qsec    vs    am 
0.167 0.070 0.096 0.143 0.298 0.168 0.150 0.256 0.171 gear  carb 
0.246 0.386 Loadings:Factor1 Factor2
mpg  -0.910         
cyl   0.962         
disp  0.946         
hp    0.851   0.364 
drat -0.726   0.418 
wt    0.867  -0.283 
qsec -0.533  -0.752 
vs   -0.783  -0.362 
am   -0.578   0.703 
gear -0.514   0.700 
carb  0.537   0.571 Factor1 Factor2
SS loadings      6.439   2.412
Proportion Var   0.585   0.219
Cumulative Var   0.585   0.805Test of the hypothesis that 2 factors are sufficient.
The chi square statistic is 68.57 on 34 degrees of freedom.
The p-value is 0.000405

相对来说，因子载荷矩阵中，各变量在第一个因子上的载荷都比较大，不好解释，需要进行因子旋转。
前两个因子的累积方差解释率达到80.5%，满足要求。

  • 进行因子旋转
> factanal(mtcars,factors = 2,rotation = "varimax")Call:
factanal(x = mtcars, factors = 2, rotation = "varimax")Uniquenesses:mpg   cyl  disp    hp  drat    wt  qsec    vs    am 
0.167 0.070 0.096 0.143 0.298 0.168 0.150 0.256 0.171 gear  carb 
0.246 0.386 Loadings:Factor1 Factor2
mpg   0.686  -0.602 
cyl  -0.629   0.731 
disp -0.730   0.609 
hp   -0.337   0.862 
drat  0.807  -0.225 
wt   -0.810   0.420 
qsec -0.162  -0.908 
vs    0.291  -0.812 
am    0.907         
gear  0.860   0.125 
carb          0.783 Factor1 Factor2
SS loadings      4.494   4.357
Proportion Var   0.409   0.396
Cumulative Var   0.409   0.805Test of the hypothesis that 2 factors are sufficient.
The chi square statistic is 68.57 on 34 degrees of freedom.
The p-value is 0.000405
  • 因子数取3
> factanal(mtcars,factors = 3,rotation = "none")Call:
factanal(x = mtcars, factors = 3, rotation = "none")Uniquenesses:mpg   cyl  disp    hp  drat    wt  qsec    vs    am 
0.135 0.055 0.090 0.127 0.290 0.060 0.051 0.223 0.208 gear  carb 
0.125 0.158 Loadings:Factor1 Factor2 Factor3
mpg  -0.910   0.137  -0.136 
cyl   0.962          -0.135 
disp  0.937  -0.174         
hp    0.875   0.292   0.147 
drat -0.689   0.453   0.175 
wt    0.858  -0.382   0.242 
qsec -0.591  -0.754   0.177 
vs   -0.809  -0.309   0.164 
am   -0.522   0.719         
gear -0.459   0.729   0.365 
carb  0.594   0.517   0.471 Factor1 Factor2 Factor3
SS loadings      6.448   2.465   0.565
Proportion Var   0.586   0.224   0.051
Cumulative Var   0.586   0.810   0.862Test of the hypothesis that 3 factors are sufficient.
The chi square statistic is 30.53 on 25 degrees of freedom.
The p-value is 0.205

此时可以发现，最大似然法在改变因子个数时，不同因子的方差贡献率发生改变（虽然改变很小），其中因子1达到58.6%，因子2达到22.4%，前两个因子累积方差贡献率为81%。

  • 因子数取3，进行因子旋转

对极大似然解，当因子数增加时，原来因子的估计载荷及对x的贡献将发生变化，这与主成分解不同。因子数可由主成分法初步确定。

> factanal(mtcars,factors = 3,rotation = "varimax")Call:
factanal(x = mtcars, factors = 3, rotation = "varimax")Uniquenesses:mpg   cyl  disp    hp  drat    wt  qsec    vs    am 
0.135 0.055 0.090 0.127 0.290 0.060 0.051 0.223 0.208 gear  carb 
0.125 0.158 Loadings:Factor1 Factor2 Factor3
mpg   0.643  -0.478  -0.473 
cyl  -0.618   0.703   0.261 
disp -0.719   0.537   0.323 
hp   -0.291   0.725   0.513 
drat  0.804  -0.241         
wt   -0.778   0.248   0.524 
qsec -0.177  -0.946  -0.151 
vs    0.295  -0.805  -0.204 
am    0.880                 
gear  0.908           0.224 
carb  0.114   0.559   0.719 Factor1 Factor2 Factor3
SS loadings      4.380   3.520   1.578
Proportion Var   0.398   0.320   0.143
Cumulative Var   0.398   0.718   0.862Test of the hypothesis that 3 factors are sufficient.
The chi square statistic is 30.53 on 25 degrees of freedom.
The p-value is 0.205

因子数取3，进行因子旋转之后，因子1的方差解释率下降到39.8%，前两个因子累积贡献率达到71.8%，发生变化。

  • 最大似然法分析
因子数有无因子旋转因子1方差贡献率因子2方差贡献率两因子累积贡献率
因子数为2无因子旋转58.5%21.9%80.5%
因子数为2有因子旋转40.9%39.6%80.5%
因子数为3无因子旋转58.6%22.4%81%
因子数为3有因子旋转39.8%32%71.8%

结论1：进行因子旋转会改变各因子的方差贡献率以及总方差贡献率
结论2：因子数不同也会改变各因子的方差贡献率

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/112953.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

微前端二：qiankun

微前端二：qiankun

qiankun是基于Single-spa开发的框架&#xff0c;所以我们先来看下Single-spa是怎么做的&#xff1a; Single-spa 是最早的微前端框架&#xff0c;兼容多种前端技术栈&#xff0c;是一个将多个单页面应用聚合为一个整体应用的 JavaScript 微前端框架&#xff1b; 优点&#xf…
阅读更多...
APP应用开发sdk版本过低可能性原因问题排查及解决方案

APP应用开发sdk版本过低可能性原因问题排查及解决方案

同学们&#xff0c;在移动 app 开发中&#xff0c;提示sdk版本过低缺找不到原因的情况都知道的吧哈哈哈&#xff0c;这个我觉得我有必要全面的分析和排查&#xff0c;让同学们看完这个文章都得以解决。这是我的初衷奈何地主家里也没有余粮呀&#xff08;我也不能完全总结出来&a…
阅读更多...
《动手学深度学习 Pytorch版》 8.7 通过时间反向传播

《动手学深度学习 Pytorch版》 8.7 通过时间反向传播

8.7.1 循环神经网络的梯度分析 本节主要探讨梯度相关问题&#xff0c;因此对模型及其表达式进行了简化&#xff0c;进行如下表示&#xff1a; h t f ( x t , h t − 1 , w h ) o t g ( h t , w o ) \begin{align} h_t&f(x_t,h_{t-1},w_h)\\ o_t&g(h_t,w_o) \end{ali…
阅读更多...
用 Python 这样去创建词云不是更美嘛？

用 Python 这样去创建词云不是更美嘛？

什么是词云&#xff1f;在网络上我们经常可以看到一张图片&#xff0c;上面有一大堆大小不一的文字&#xff0c;这便是词云。词云一般是根据输入的大量词语生成的&#xff0c;如果某个词语出现的次数越多&#xff0c;那么相应的大小就会越大。 Python 中有一个专门用来生成词云…
阅读更多...
智慧公厕：打造未来城市公共设施的智慧选择

智慧公厕：打造未来城市公共设施的智慧选择

随着信息技术的不断发展&#xff0c;城市公共设施需要实现个性化、高效化和智能化&#xff0c;其中包括公共厕所。智慧公厕是一种结合物联网、互联网、人工智能、云计算、大数据和传感感知等技术的新型公厕&#xff0c;旨在提高公共厕所管理效率、跨区域跨系统的联网管理、自动…
阅读更多...
【C++入门 一 】学习C++背景、开启C++奇妙之旅

【C++入门 一 】学习C++背景、开启C++奇妙之旅

目录 1.什么是C2. C的发展史3. C的重要性3.1 语言的使用广泛度3.2 在工作领域1. 操作系统以及大型系统软件开发2. 服务器端开发3. 游戏开发4. 嵌入式和物联网领域5. 数字图像处理6. 人工智能7. 分布式应用 3.3 在校招领域3.3.1 岗位需求3.3.2 笔试题 4. 如何学习C4.1 别人怎么学…
阅读更多...
WAL 模式（PostgreSQL 14 Internals翻译版）

WAL 模式（PostgreSQL 14 Internals翻译版）

性能 当服务器正常运行时&#xff0c;WAL文件不断被写入磁盘。但是&#xff0c;这些写操作是顺序的:几乎没有随机访问&#xff0c;因此即使是HDD也可以处理这个任务。由于这种类型的加载与典型的数据文件访问非常不同&#xff0c;因此有必要为WAL文件设置一个单独的物理存储&a…
阅读更多...
数据结构之堆

数据结构之堆

目录 前言 堆的概念与结构 堆的实现 堆的初始化 堆的销毁 堆的显示 堆的插入 堆的向上调整算法 堆的删除 堆的向下调整算法 堆的判空 获取堆顶元素 堆的数据个数 堆的创建 前言 二叉树的顺序结构存储即使用数组存储&#xff0c;而数组存储适用于完全二叉树&#xf…
阅读更多...
【具身智能综述1】A Survey of Embodied AI: From Simulators to Research Tasks

【具身智能综述1】A Survey of Embodied AI: From Simulators to Research Tasks

论文标题&#xff1a;A Survey of Embodied AI: From Simulators to Research Tasks 论文作者&#xff1a;Jiafei Duan, Samson Yu, Hui Li Tan, Hongyuan Zhu, Cheston Tan 论文原文&#xff1a;https://arxiv.org/abs/2103.04918 论文出处&#xff1a;IEEE Transactions on E…
阅读更多...
柯桥银泰附近有学德语的地方吗，留学德语培训

柯桥银泰附近有学德语的地方吗，留学德语培训

01 die Garantiefr jemandem/etwas 给某人或某事的保障 Das System bietet die Garantie fr die Bauer. 02 der Gebrauch von etwas 使用某物 Wir haben den Gebrauch vom Computer gelerbt. 我们学会了使用电脑。 03 Die Geduld mit jemandem/etwas 对..的耐心 Der Lehre…
阅读更多...
智慧河湖方案：AI赋能水利水务，构建河湖智能可视化监管大数据平台

智慧河湖方案：AI赋能水利水务，构建河湖智能可视化监管大数据平台

一、方案背景 我国江河湖泊众多&#xff0c;水系发达。伴随着经济社会快速发展&#xff0c;水生态水环境问题成为群众最关注的民生议题之一。一些河流开发利用已接近甚至超出水环境承载能力&#xff0c;一些地区废污水排放量居高不下&#xff0c;一些地方侵占河道、围垦湖泊等…
阅读更多...
如何在不恢复出厂设置的情况下解锁 Android 手机密码？

如何在不恢复出厂设置的情况下解锁 Android 手机密码？

如何在不恢复出厂设置的情况下解锁 Android 手机密码&#xff1f; 当您忘记 Android 手机的密码时&#xff0c;可能会有压力&#xff0c;尤其是当您不想恢复出厂设置并删除所有数据时。但是&#xff0c;有一些方法可以在不诉诸如此激烈的步骤的情况下解锁手机。我们将在这篇文…
阅读更多...
数据仓库扫盲系列（1）：数据仓库诞生原因、基本特点、和数据库的区别

数据仓库扫盲系列（1）：数据仓库诞生原因、基本特点、和数据库的区别

数据仓库的诞生原因 随着互联网的普及&#xff0c;信息技术已经深入到各行各业&#xff0c;并逐步融入到企业的日常运营中。然而&#xff0c;当前企业在信息化建设过程中遇到了一些困境与挑战。 1、历史数据积存。 过去企业的业务系统往往是在较长时间内建设的&#xff0c;很…
阅读更多...
JavaSE编程题目练习（三）

JavaSE编程题目练习（三）

博客昵称&#xff1a;架构师Cool 最喜欢的座右铭&#xff1a;一以贯之的努力&#xff0c;不得懈怠的人生。 作者简介&#xff1a;一名Coder&#xff0c;欢迎关注小弟&#xff01; 博主小留言&#xff1a;哈喽&#xff01;各位CSDN的uu们&#xff0c;我是你的小弟Cool&#xff0…
阅读更多...
2023.10.20期中考核复现（misc）

2023.10.20期中考核复现（misc）

杂项题就是2023陇剑杯的题目&#xff0c;可能还是不感兴趣吧&#xff0c;自从打完蓝帽杯之后除了web以外什么都没看 flow analysis 1 题目&#xff1a;What is the backdoor file name that comes with the server?( Including file suffix) 服务器附带的后门文件名是什么&am…
阅读更多...
【前端】图片裁剪路径绘制及图片不规则裁剪

【前端】图片裁剪路径绘制及图片不规则裁剪

说明 项目中可能需要用户根据展示的图片&#xff0c;然后绘制需要裁剪的路径&#xff0c;再根据绘制的坐标进行裁剪&#xff0c;以下是前端的裁剪路径绘制的代码示例&#xff0c;后端可以根据当前的获取到的坐标进行裁剪&#xff0c;裁剪的坐标保存在coordinate数组中。 代码 …
阅读更多...
【Maven教程】（八）：使用 Nexus 创建私服 ~

【Maven教程】（八）：使用 Nexus 创建私服 ~

Maven 使用 Nexus 创建私服 1️⃣ Nexus简介2️⃣ 安装 Nexus2.1 下载 Nexus2.2 Bundle 方式安装 Nexus2.3 WAR 方式安装 Nexus2.4 登录 Nexus 3️⃣ Nexus 的仓库与仓库组3.1 Nexus 内置的仓库3.2 Nexus 仓库分类的概念3.3 创建 Nexus 宿主仓库3.4 创建 Nexus 代理仓库3.5 创…
阅读更多...
计算机毕业设计 基于SpringBoot笔记记录分享网站的设计与实现 Javaweb项目 Java实战项目 前后端分离 文档报告 代码讲解 安装调试

计算机毕业设计 基于SpringBoot笔记记录分享网站的设计与实现 Javaweb项目 Java实战项目 前后端分离 文档报告 代码讲解 安装调试

&#x1f34a;作者&#xff1a;计算机编程-吉哥 &#x1f34a;简介&#xff1a;专业从事JavaWeb程序开发&#xff0c;微信小程序开发&#xff0c;定制化项目、 源码、代码讲解、文档撰写、ppt制作。做自己喜欢的事&#xff0c;生活就是快乐的。 &#x1f34a;心愿&#xff1a;点…
阅读更多...
openGauss学习笔记-105 openGauss 数据库管理-管理用户及权限-默认权限机制

openGauss学习笔记-105 openGauss 数据库管理-管理用户及权限-默认权限机制

文章目录 openGauss学习笔记-105 openGauss 数据库管理-管理用户及权限-默认权限机制 openGauss学习笔记-105 openGauss 数据库管理-管理用户及权限-默认权限机制 数据库对象创建后&#xff0c;进行对象创建的用户就是该对象的所有者。openGauss安装后的默认情况下&#xff0c…
阅读更多...
C++算法前缀和的应用：分割数组的最大值的原理、源码及测试用例

C++算法前缀和的应用：分割数组的最大值的原理、源码及测试用例

分割数组的最大值 相关知识点 C算法&#xff1a;前缀和、前缀乘积、前缀异或的原理、源码及测试用例&#xff1a;付视频课程 二分 过些天整理基础知识 题目 给定一个非负整数数组 nums 和一个整数 m &#xff0c;你需要将这个数组分成 m 个非空的连续子数组。 设计一个算法…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023