一、OFDM简述
OFDM 的全称是 Orthogonal Frequency Divisition Multiplexing,是一种多载波调制技术,其能有效对抗频率选择性衰落,克服信号符号间干扰。OFDM的技术的核心思想是将宽频率载波划分成多个带宽较小的正交子载波,并使用这些正交子载波发送及接收信号。
- Orthogonal :正交的
- Frequency Divisition:频率划分的
- Multiplexing:复用
OFDM频域示意图
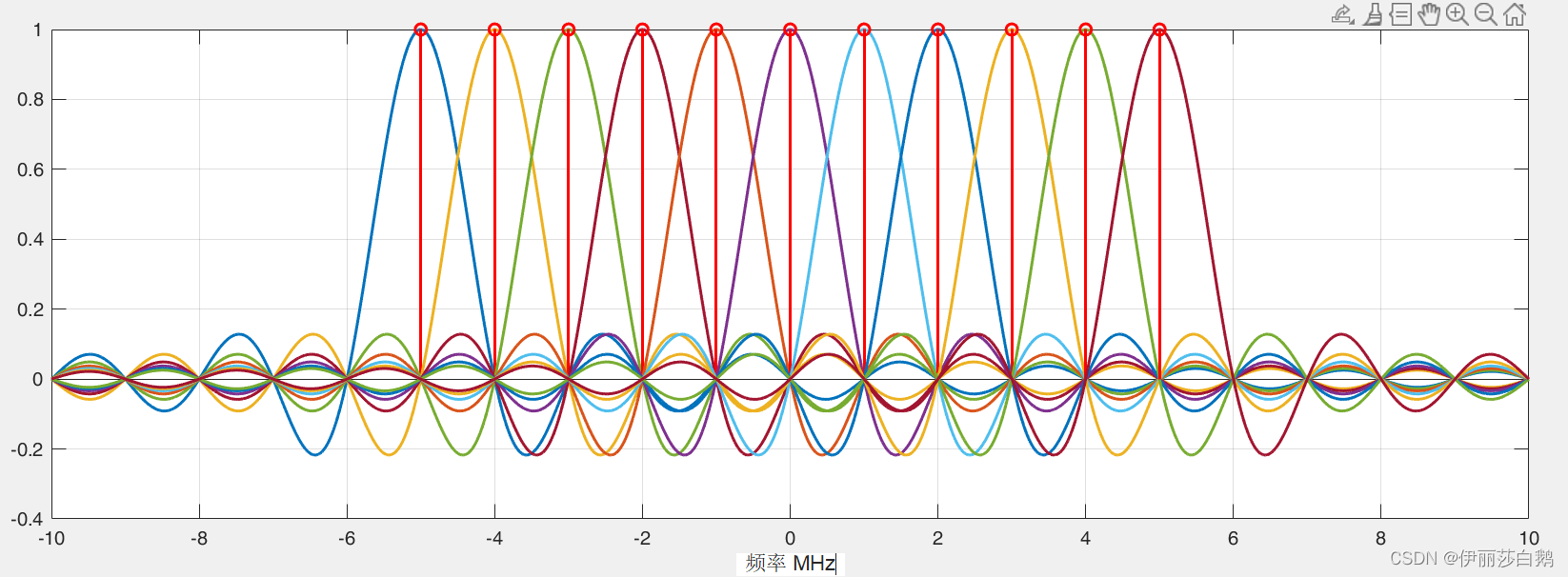
OFDM时域示意图
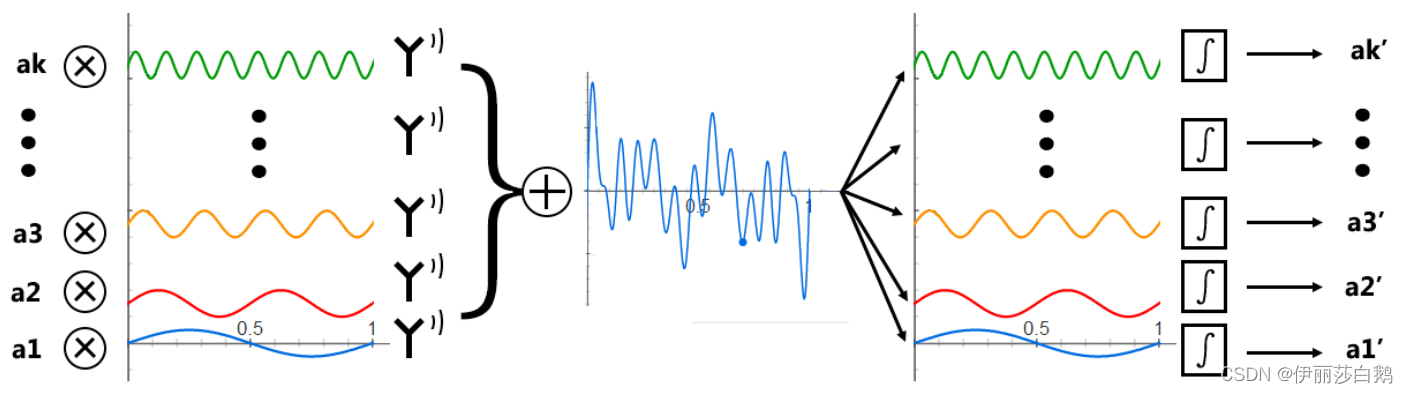
二、OFDM的正交性
1、正交性的定义
正交性是OFDM信号实现无ICI(载波间干扰)的必要条件。基本的数学定义为,考虑时间有限的复指数信号 { e j 2 π f k t } k = 0 N − 1 \left\{\mathrm{e}^{\mathrm{j} 2 \pi f_k t}\right\}_{k=0}^{N-1} {ej2πfkt}k=0N−1, 它们表示 OFDM 信号中在 f k = k / T s y m f_k=k / T_{\mathrm{sym}} fk=k/Tsym 的不同子载波( 0 ⩽ t ⩽ T sym 0\leqslant t \leqslant T_{\text {sym }} 0⩽t⩽Tsym ) 。如果这些信号的乘积在它们的公共 (基本) 周期内的积分为零, 那么它们被定是正交的, 即
1 T sym ∫ 0 T sym e j 2 π f k t e − j 2 π f i t d t = 1 T sym ∫ 0 T sym e j 2 π k T sym t e − j 2 π i T sym t d t = 1 T sym ∫ 0 T sym e j 2 π ( k − i ) T sym t d t = { 1 , ∀ k = i 0 , 其他 \begin{aligned} \frac{1}{T_{\text {sym }}} \int_0^{T_{\text {sym }}} \mathrm{e}^{\mathrm{j} 2 \pi f_k t} \mathrm{e}^{-\mathrm{j} 2 \pi f_i t} \mathrm{~d} t & =\frac{1}{T_{\text {sym }}} \int_0^{T_{\text {sym }}} \mathrm{e}^{\mathrm{j} 2 \pi \frac{k}{T_{\text {sym }}} t} \mathrm{e}^{-\mathrm{j} 2 \pi \frac{i}{T_{\text {sym }}} t} \mathrm{~d} t \\ & =\frac{1}{T_{\text {sym }}} \int_0^{T_{\text {sym }}} \mathrm{e}^{\mathrm{j} 2 \pi \frac{(k-i)}{T_{\text {sym }} t}} \mathrm{~d} t \\ & = \begin{cases}1, & \forall k=i \\ 0, & \text { 其他 }\end{cases} \end{aligned} Tsym 1∫0Tsym ej2πfkte−j2πfit dt=Tsym 1∫0Tsym ej2πTsym kte−j2πTsym it dt=Tsym 1∫0Tsym ej2πTsym t(k−i) dt={1,0,∀k=i 其他
2、正交性的作用
首先频分复用相当于提高频带的利用率,正交频分复用则可以使频带的利用率达到理论上的最大值,并且子载波的正交性保证了无ICI的情况。图中上半部分是普通的频分复用;图中下半部分两个子载波正交,此时一个载波的旁瓣在另一个载波上值为0。
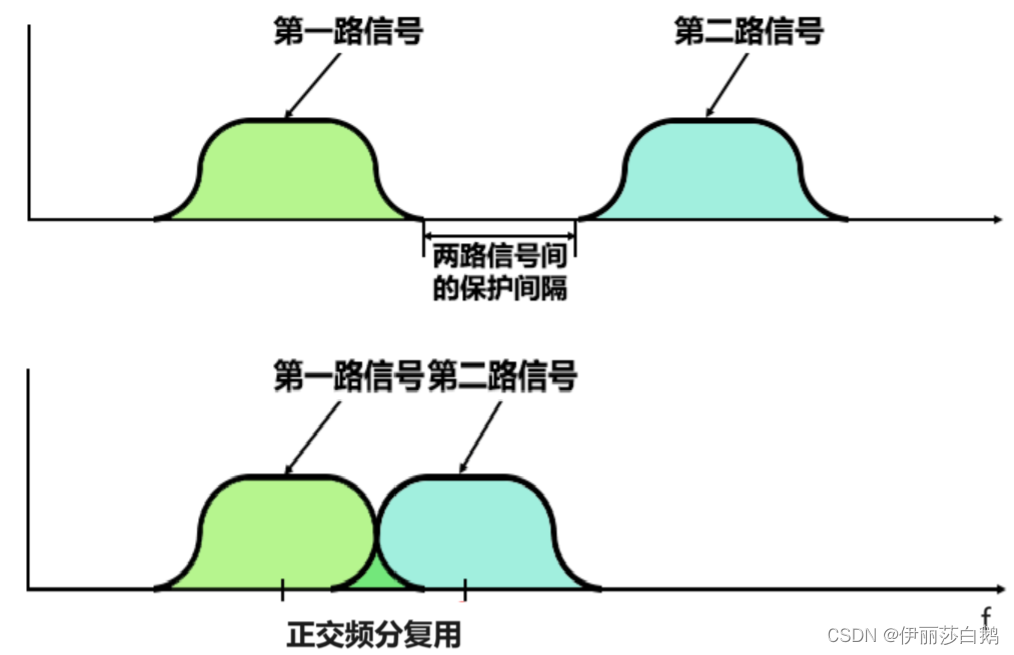
三、OFDM的调制解调
OFDM调制的过程将信息比特流映射成一个PSK或 QAM 符号序列,之后将符号序列转换为N个并行符号流。每N个经过串/并转换的符号被不同的子载波调制。解调过程基本为调制逆过程。
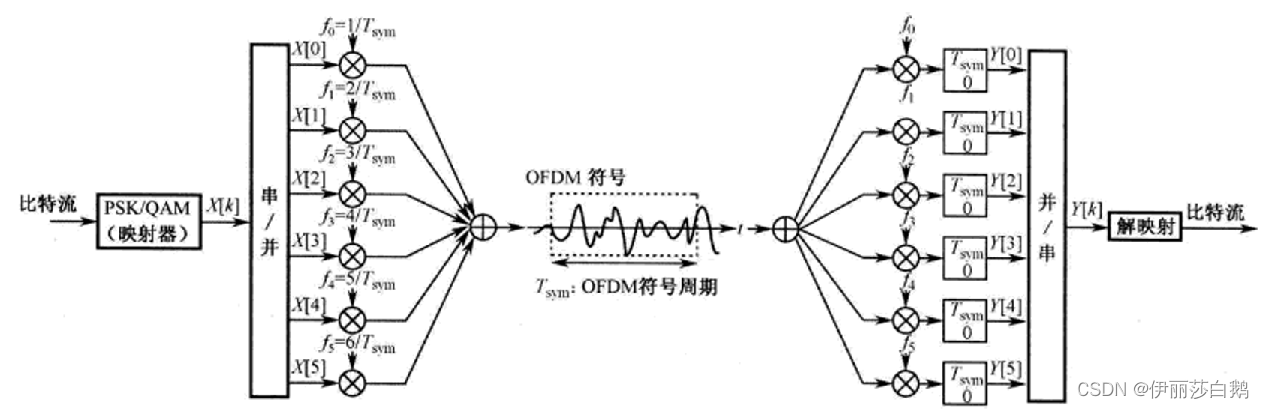
1、公式推理OFDM实现
公式推导未考虑噪声影响
OFDM调制
OFDM 发射机将信息比特流映射成一个 PSK 或 QAM 符号序列, 之后将符号序列转换为 N N N 个并行符号流。每 N N N 个经过串/并转换的符号被不同的子载波调制。令 X I [ k ] X_I[k] XI[k] 表示在第 k k k 个子载波上的第 l l l 个发送符号, l = 0 , 1 , 2 , ⋯ , ∞ , k = 0 , 1 , 2 , ⋯ , N − 1 l=0,1,2, \cdots, \infty, k=0,1,2, \cdots, N-1 l=0,1,2,⋯,∞,k=0,1,2,⋯,N−1 。由于串/并转换, N N N 个符号的传输时间扩展为 N T s N T_{\mathrm{s}} NTs(N个符号生成) , 它即是单个 OFDM 符号的持续时间 T s y m T_{\mathrm{sym}} Tsym 即 T s y m = N T s T_{\mathrm{sym}}=N T_{\mathrm{s}} Tsym=NTs 。
令 Ψ l , k ( t ) \Psi_{l, k}(t) Ψl,k(t) 表示在第 k k k 个子载波上的第 l l l 个 OFDM 信号:
Ψ l , k ( t ) = { e j 2 π f k ( t − l T sym ) , 0 < t ⩽ T sym 0 , 其他 \Psi_{l, k}(t)= \begin{cases}\mathrm{e}^{\mathrm{j} 2 \pi f_k\left(t-l T_{\text {sym }}\right)}, & 0<t \leqslant T_{\text {sym }} \\ 0, & \text { 其他 }\end{cases} Ψl,k(t)={ej2πfk(t−lTsym ),0,0<t⩽Tsym 其他
则OFDM基带信号可以表示
x l ( t ) = ∑ l = 0 ∞ ∑ k = 0 N − 1 X l [ k ] e j 2 π f k ( t − l T s y m ) x_l(t)=\sum_{l=0}^{\infty} \sum_{k=0}^{N-1} X_l[k] \mathrm{e}^{\mathrm{j} 2 \pi f_k\left(t-l T_{\mathrm{sym}}\right)} xl(t)=l=0∑∞k=0∑N−1Xl[k]ej2πfk(t−lTsym)
在时刻 t = l T s y m + n T s , T s = T s y m / N , f k = k / T s y m t=l T_{\mathrm{sym}}+n T_{\mathrm{s}}, T_{\mathrm{s}}=T_{\mathrm{sym}} / N, f_k=k / T_{\mathrm{sym}} t=lTsym+nTs,Ts=Tsym/N,fk=k/Tsym, 对时间 OFDM 信号进行采样,可以得到相应的离散时间的 OFDM 符号:
x l [ n ] = ∑ k = 0 N − 1 X l [ k ] e j 2 π k n / N n = 0 , 1 , ⋯ , N − 1 x_l[n]=\sum_{k=0}^{N-1} X_l[k] \mathrm{e}^{\mathrm{j} 2 \pi k n / N}\quad n=0,1, \cdots, N-1 xl[n]=k=0∑N−1Xl[k]ej2πkn/Nn=0,1,⋯,N−1
可以证明式 x l [ n ] x_l[n] xl[n]是 PSK 或 QAM 数据符号 { X l [ k ] } k = 0 N − 1 \left\{X_l[k]\right\}_{k=0}^{N-1} {Xl[k]}k=0N−1 的 N N N 点 IDFT,利用 IFFT 算法可以快速计算。
OFDM解调
基带 OFDM 接收符号 y l ( t ) = ∑ k = 0 N − 1 X l [ k ] e j 2 π f k ( t − l T s y m ) , l T s y m < t < l T s y m + n T s y_l(t)=\sum_{k=0}^{N-1} X_l[k] \mathrm{e}^{\mathrm{j} 2 \pi f_k\left(t-l T_{\mathrm{sym}}\right)}, l T_{\mathrm{sym}}<t<l T_{\mathrm{sym}}+n T_{\mathrm{s}} yl(t)=∑k=0N−1Xl[k]ej2πfk(t−lTsym),lTsym<t<lTsym+nTs 。
利用子载波 e j 2 π f k ( t − l T sym ) \mathrm{e}^{\mathrm{j} 2 \pi f_k\left(t-l T_{\text {sym }}\right)} ej2πfk(t−lTsym )的正交性,可以重构原发送符号 X l [ k ] X_l[k] Xl[k] :
Y l [ k ] = 1 T sym ∫ − ∞ ∞ ∑ i = 0 N − 1 { X l [ i ] e j 2 π f i ( t − l T sym ) } e − j 2 π f k ( t − l T sym ) d t = ∑ i = 0 N − 1 X l [ i ] { 1 T sym ∫ 0 T sym e j 2 π ( f i − f k ) ( t − l T s y m ) d t } = X l [ k ] \begin{aligned} Y_l[k] & =\frac{1}{T_{\text {sym }}} \int_{-\infty}^{\infty} \sum_{i=0}^{N-1}\left\{X_l[i] \mathrm{e}^{\mathrm{j} 2 \pi f_i\left(t-l T_{\text {sym }}\right)}\right\} \mathrm{e}^{-\mathrm{j} 2 \pi f_k\left(t-l T_{\text {sym }}\right)} \mathrm{d} t \\ & =\sum_{i=0}^{N-1} X_l[i]\left\{\frac{1}{T_{\text {sym }}} \int_0^{T_{\text {sym }}} \mathrm{e}^{\mathrm{j} 2 \pi\left(f_i-f_k\right)\left(t-l T_{\mathrm{sym}}\right)} \mathrm{d} t\right\}=X_l[k] \end{aligned} Yl[k]=Tsym 1∫−∞∞i=0∑N−1{Xl[i]ej2πfi(t−lTsym )}e−j2πfk(t−lTsym )dt=i=0∑N−1Xl[i]{Tsym 1∫0Tsym ej2π(fi−fk)(t−lTsym)dt}=Xl[k]
令 { y l [ n ] } n = 0 N − 1 \left\{y_l[n]\right\}_{n=0}^{N-1} {yl[n]}n=0N−1 为 OFDM 接收符号 y l ( t ) y_l(t) yl(t) 在 t = l T s y m + n T s t=l T_{\mathrm{sym}}+n T_{\mathrm{s}} t=lTsym+nTs时刻的采样。调制过程的积分可以表示为下面的离散时域形式:
Y l [ k ] = 1 N ∑ n = 0 N − 1 ∑ i = 0 N − 1 X l [ i ] e j 2 π ( i − k ) n / N = X l [ k ] \begin{aligned} Y_l[k] & =\frac{1}{N} \sum_{n=0}^{N-1} \sum_{i=0}^{N-1} X_l[i] \mathrm{e}^{\mathrm{j} 2 \pi(i-k) n / N}=X_l[k] \end{aligned} Yl[k]=N1n=0∑N−1i=0∑N−1Xl[i]ej2π(i−k)n/N=Xl[k]
可以证明 Y l [ k ] Y_l[k] Yl[k] 是 { y l [ n ] } n = 0 N − 1 \left\{y_l[n]\right\}_{n=0}^{N-1} {yl[n]}n=0N−1 的 N N N 点 DFT,利用 FFT 算法进行快速计算。
2、OFDM 中的保护间隔–CP(Cyclic Prefix)
多径衰落信道会使得传输的信号存在时延拓展,对OFDM的传输影响未ISI和ICI。对于ISI(符号间干扰),只要前一个符号经过时延扩展后会对下一个符号产生影响。对于ICI(信号间干扰),由于信道是多径信道,各路子载波被接收到的时间可能有偏差,这就造成在FFT积分时间长度内子载波之间相差不再是整数周期,正交性被破坏.
循环前缀(CP) 实现OFDM 符号的循环扩展(为了信号连续性)。将 OFDM 符号后部的采样复制到其前面,实现CP对OFDM符号的扩展。
OFDM通过添加循环前缀解决这两个问题:
- 消除ISI:当信道的冲激相应长度小于CP的长度时,延时的前一个符号没有机会进入后一个符号的区间来影响,从而可以消除ISI。
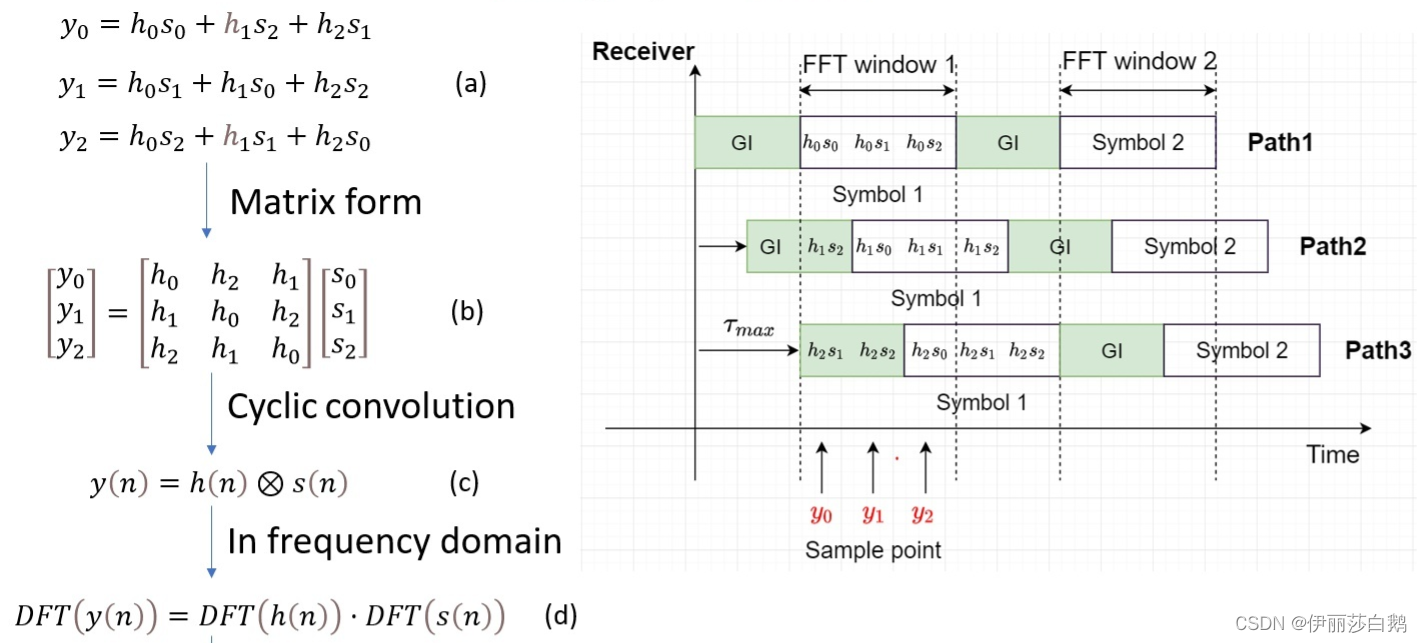
- 消除ICI:单纯在保护间隔补0仍然无法保证子载波的正交性,采用循环前缀后,信道输出的后N个样值是发送序列和信道冲激响应的循环卷积,有了循环前缀避免了混叠,从而可以消除ICI。
从图上可以很清楚的看出 CP 的加入如何转换成循环卷积
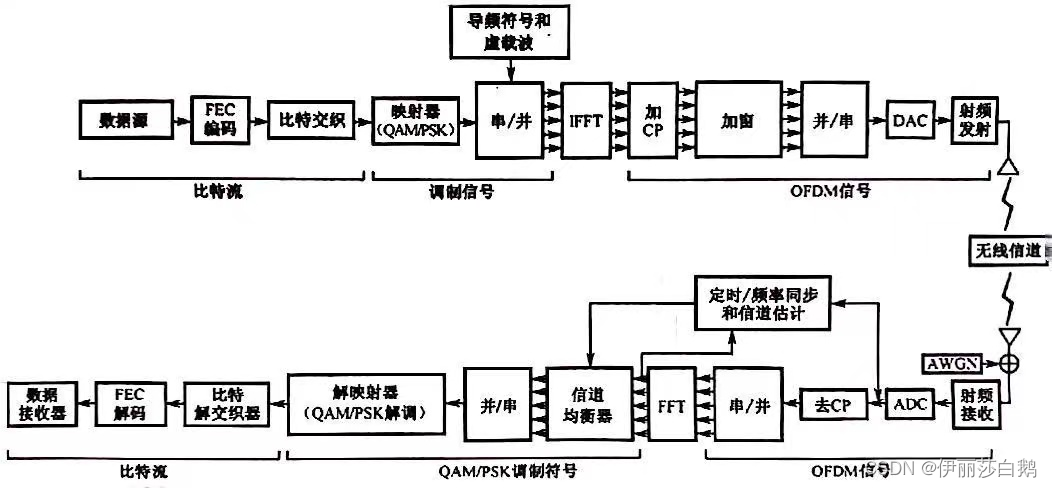
3、OFDM实现框图
接收部分的时间和频率同步以及信道估计与均衡也是OFDM中的重要技术
参考资料
无线通信基础2:深入理解OFDM(含Matlab代码)
快速傅里叶变换(FFT)和逆快速傅里叶变换(IFFT)
给“小白”图示讲解OFDM的原理
OFDM的ISI和CP(循环前缀)
浅谈对OFDM的理解
《MIMO-OFDM无线通信技术及MATLAB实现》



)








)
-NOA领航辅助系统-集度)





之less)