卓里奇书好的一点就是，不是直接引出公式，而是告诉你理由。先引出正交的概念，然后在函数空间中，也有正交，只不过是无限维的空间。

 这里要注意，明确说明了是有限个。

在函数空间里面，内积是指进行积分，同时会对第二个变量取共轭。

 

这里涉及到对复数的积分。暂时先不考虑里面的细节。

 这里引出了斯密特正交化。

这里看到了熟悉的名字，勒让德，首先它的基是多项式，但遗憾的是这些多项式并不是正交的，知识线性无关的。要变成正交的会需要进行处理。

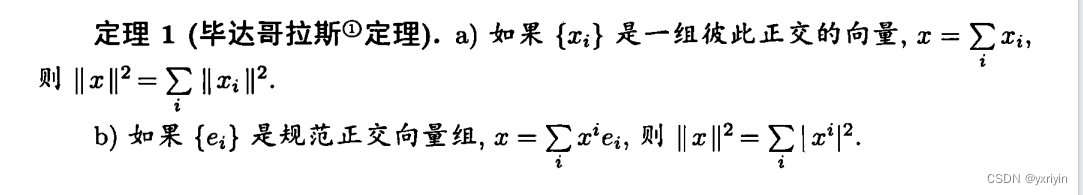
这其实就是勾股定理。

 在非单位的情况下，我们需要除以基的长度，这样也能得到对应的傅里叶系数。

 

要注意，贝塞尔不等式是：

 

 后面内容我觉得老师的说法特别好：

我们普通的级数展开，没有傅里叶展开这么好。为什么呢，比如泰勒展开，它的基并不是正交的，而傅里叶展开的基，是正交的，正交的好处是，我们利用勾股定理，可以确认一个上界，让这些都是收敛的。