前言
堆是计算机科学中-类特殊的数据结构的统称。实现有很多,例如:大顶堆,小顶堆,斐波那契堆,左偏堆,斜堆等等。从子结点个数上可以分为二汊堆,N叉堆等等。本文将介绍的是二叉堆。
二叉堆的概念
1、引例

我们小时候,基本都玩过或见过叠罗汉的恶作剧(如上图)。叠罗汉运动是把人堆在一起,而且为了保证稳定性,体重大身高高的人一般在下面,体重轻身高矮的人一般在上面,我们的二叉堆结构也是按照某种规则把元素堆成一个塔形结构。
2、定义

二叉堆是具有下列性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆( 例如左上图所示) ;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆(例如右上图所示)。
3、性质
对于大(小)顶堆,它总是满足下列性质:
1)空树是一个大(小)顶堆;
2)大(小)顶堆中某个结点的关键字小(大)于等于其父结点的关键字;
3)大(小)顶堆是一棵完全二叉树。
4)根结点一定是大(小)顶堆中所有结点最大(小)者。
4、作用
二叉堆能够在O(1)的时间内,获得关键字最大(小)的元素。并且能够在O(logn)的时间内执行插入和删除。一般用来做优先队列的实现、堆排序算法等。
堆的存储结构
二叉堆是一颗完全二叉树,是一种树形结构,但是我们未必真的需要按照二叉树的存储方式去实现,类似于并查集用数组来模拟树形结构,我们的二叉堆类似的,把每个结点,按照层序映射到-一个顺序存储的数组中,然后利用每个结点在数组中的下标,来确定结点之间的关系。
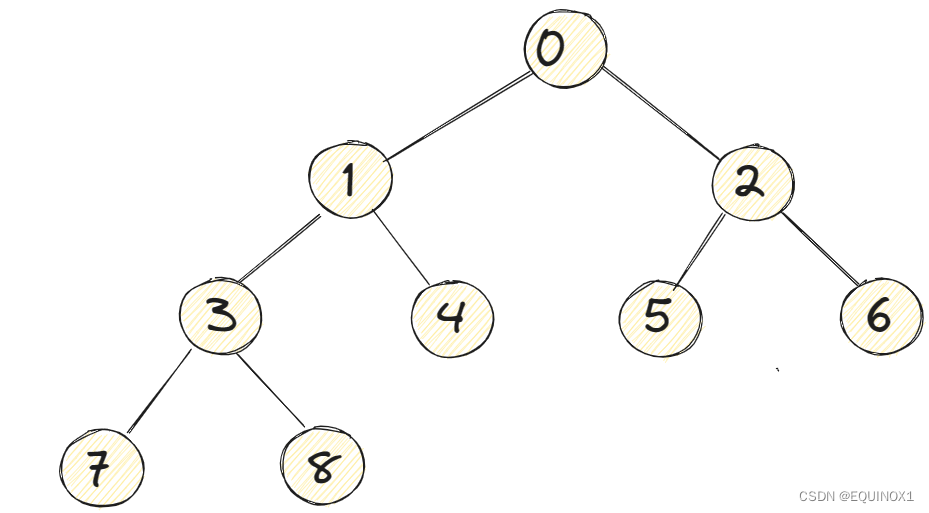
结点的编号
根节点
在国内的数据结构教材中,有的把根节点编号为0,有的编号为1,这里我们选择编号为0。
孩子结点
根据上图示例结合我们二叉树的性质,不难发现
根节点和左右孩子编号关系为:lchild = parent * 2 + 1 rchild = parent * 2 +2
同样的parent = (lchild - 1) / 2 = (rchild - 1) / 2(利用C/C++除法向下取整)
存储结构
对于堆,显然我们需要一个容器来存储我们的数据,由于堆的建造过程中我们难以避免大小比较,我们不妨增加一个比较的仿函数作为模板参数
存储结构如下
template <class T, class Container = vector<T>, class Compare = less<T>>
//T为存储数据类型 Container为存储数据的容器,默认为vector Compare为两关键字进行比较的仿函数,可由用户自定义传入
class Heap{//...
private:Container _con;Compare _cmp;
};
堆的构造
向下调整算法
我们给定这样一个情形,有一颗根节点不满足堆规则但是其他任意子树都满足二叉堆规则的完全二叉树,我们进行怎样的调整可以使它成为堆?
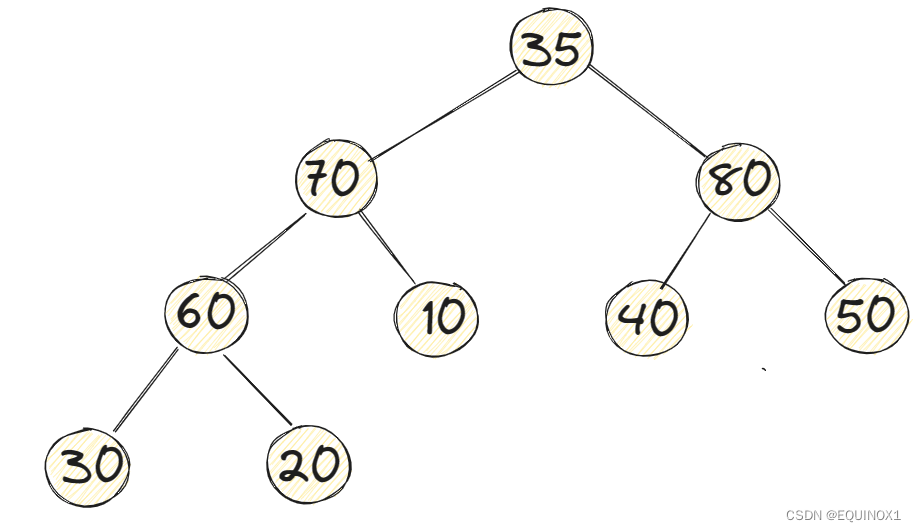
如上图示例大顶堆,根节点35小于80和70,但是其他子树都符合我们大顶堆的规则,我们该如何调整呢?
需要从孩子中选择一个节点来替代我们的根节点,为了尽可能保证大顶堆的特性,我们选择孩子节点中最大的80和35进行交换,但是交换完之后根节点是符合规则了,交换后的35又小于40和50,这时除了35所在子树其他子树都满足大顶堆的特性,所以我们继续对35的子树进行调整,再次与最大孩子节点交换,我们发现这时得到了一个大顶堆。
我们向下调整算法调整的初始节点满足除了初始节点和子节点不满足堆规则,其他节点都满足。而我们每次调整会修正当前位置,同时最多增加一个不满足规则的位置,也就是说最多调整高度次,时间复杂度为O(log(N + 1)) = O(logN)
代码如下:
void AdjustDown(int parent){int child = parent * 2 + 1;int n = _con.size();while (child < n){if (child + 1 < n && _cmp(_con[child], _con[child + 1])){child++;}if (_cmp(_con[parent], _con[child])){swap(_con[parent], _con[child]);parent = child;child = parent * 2 + 1;}elsebreak;}}
向上调整算法
会了向下调整算法,自然就会向上调整算法了
同样的,我们向上调整算法调整的初始节点满足除了初始节点和父节点不满足堆规则,其他节点都满足。而我们每次调整会修正当前位置,同时最多增加一个不满足规则的位置,最多调整高度次,时间复杂度为O(log(N + 1)) = O(logN)
这里只给出大根堆示例就不详细说明了

代码如下:
void AdjustUp(int child){int parent = (child - 1) / 2;while (parent >= 0){if (_cmp(_con[parent], _con[child])){swap(_con[parent], _con[child]);child = parent;parent = (parent - 1) / 2;}elsebreak;}}
堆的构建算法
基于AdjustDown的自底而上构建
我们实际中,大多数时候都不会像两种调整算法那么巧,只有一个位置不符合规则,那么对于任意元素集合,我们该如何来进行调整呢?
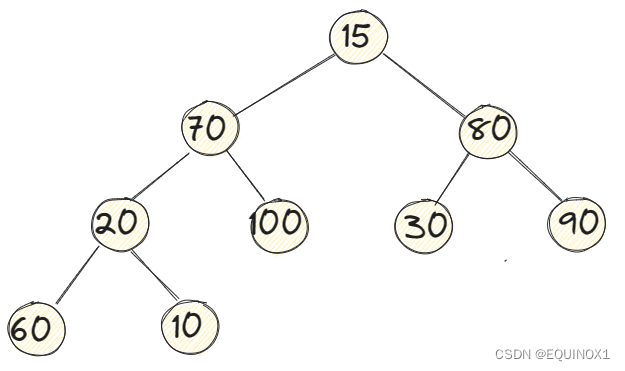
比如上图,就是一种很不符合我们堆规则的情形,而我们只会两种调整算法的情形处理方式,但是我们可以把一个堆看成多个堆的组合
我们以向下调整算法为例我们按照下标顺序,从第一个非叶子节点开始从后往前执行向下调整算法,会出现什么情况呢?
为了更好理解,这里使用动画演示

对于我们的开始节点,也就是第一个非叶子节点20它显然符合我们向下调整算法的情形,Adjustdown后20节点所在子树修正完毕,然后向前继续该操作,修正节点80,然后修正节点70最后到根节点15的时候我们发现15此时也符合我们Adjustdown的情形,再次Adjustdown后,我们得到了一颗大根堆
现在我们清楚了,我们的向下调整堆构建算法就是从自下而上不断的修正,直到出现只有根节点不符合堆的规则,再次Adjustdown后我们就得到了堆
时间复杂的的计算我们后面详细解释
代码如下:
void BuildHeap()
{
for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(i);}
}
基于AdjustUp的自顶而下构建
会了基于AdjustDown的自底而上构建,自然会基于AdjustUp的自顶而下构建辣。
这里直接给出代码:
void BuildHeap()
{
for (int i = 0; i <= (n - 1 - 1) / 2; i++){AdjustUp(i);}
}
两种构建算法的时间复杂度分析
前面没有给出两种构建的时间复杂度分析,是为了专门在这里说明,从而进行两种方法的选择。
对于基于AdjustDown的自底而上构建
这里给出计算方法
总调整次数为每一层节点数量乘该层每个节点调整次数求和
假设高度为h,对于第i层,有2^i次方个节点,需要调整(h - i)次,根据高中数列求和的知识,不难完成F(h)的计算
F ( h ) = 2 h − 1 × 0 + 2 h − 2 × 1 + ⋯ + 2 0 × ( h − 1 ) ① 2 ∗ F ( h ) = 2 h × 0 + 2 h − 2 × 1 + ⋯ + 2 0 × ( h − 1 ) ② F ( h ) = 2 h − 1 + 2 h − 2 + ⋯ + 2 0 − h + 2 ② − ① = 2 h − 1 − h − 1 = N − log 2 ( N + 1 ) ≈ N \begin{equation} \begin{split} F(h)&=2^{h-1}\times 0+2^{h-2}\times 1+\dots +2^{0} \times(h - 1) ①\\ 2*F(h)&=2^{h}\times 0+2^{h-2}\times 1+\dots +2^{0} \times(h - 1) ②\\ F(h)&=2^{h-1}+2^{h-2}+\dots +2^{0}-h+2②-①\\ &=2^{h-1}-h-1\\ &=N-\log_{2}{(N+1)} \\ &\approx N \end{split} \end{equation} F(h)2∗F(h)F(h)=2h−1×0+2h−2×1+⋯+20×(h−1)①=2h×0+2h−2×1+⋯+20×(h−1)②=2h−1+2h−2+⋯+20−h+2②−①=2h−1−h−1=N−log2(N+1)≈N
对于基于AdjustUp的自顶而下构建
F ( h ) = 2 1 − 1 × 0 + 2 2 − 1 × 1 + ⋯ + 2 h − 1 × ( h − 1 ) ① 2 ∗ F ( h ) = 2 1 × 0 + 2 2 × 1 + ⋯ + 2 h × ( h − 1 ) ② F ( h ) = 2 h × ( h − 1 ) − 2 h + 1 ② − ① = 2 h × ( h − 2 ) − h + 1 = ( N + 1 ) × ( log 2 N − 1 ) − log 2 ( N + 1 ) + 1 = N × log 2 N − N ≈ N × log 2 N \begin{equation} \begin{split} F(h)&=2^{1-1}\times 0+2^{2-1}\times 1+\dots +2^{h-1} \times(h-1) ①\\ 2*F(h)&=2^{1}\times 0+2^{2}\times 1+\dots +2^{h} \times(h-1) ②\\ F(h)&=2^{h}\times(h-1)-2^{h}+1②-①\\ &=2^{h}\times(h-2)-h+1\\ &=(N+1)\times(\log_{2}{N} - 1)-\log_{2}{(N+1)}+1 \\ &=N\times\log_{2}{N}-N\\ &\approx N\times\log_{2}{N} \end{split} \end{equation} F(h)2∗F(h)F(h)=21−1×0+22−1×1+⋯+2h−1×(h−1)①=21×0+22×1+⋯+2h×(h−1)②=2h×(h−1)−2h+1②−①=2h×(h−2)−h+1=(N+1)×(log2N−1)−log2(N+1)+1=N×log2N−N≈N×log2N
通过对比发现,自底而上构建为O(N),而自顶而下构建为O(NlogN),所以我们一般选择自底而上构建
堆的常用接口
实际上,我们如果不以序列初始化堆的话,是用不到堆的构建算法的,因为每次只涉及堆的一个元素的增删查改,下面介绍我们堆的常用接口的实现
堆的插入push
对于在堆里面新增元素,我们尾插,然后此时对新元素向上调整即可
void push(const T &x){_con.push_back(x);AdjustUp(_con.size() - 1);}
堆顶元素的删除pop
对于删除堆顶元素,我们把堆顶元素和序列是容器中最后一个元素交换然后尾删,但是此时堆顶可能非法,所以还要对堆顶向下调整
void pop(){swap(_con[0], _con[_con.size() - 1]);_con.pop_back();AdjustDown(0);}
获取堆顶元素top
直接返回堆顶即可
T top() const{return _con[0];}
堆是否为空empty
调用序列是容器的接口即可
bool empty() const{return _con.empty();}
获取堆的大小size
同样调用序列式容器的接口
bool size() const{return _con.size();}
堆的代码实现
template <class T, class Container = vector<T>, class Compare = less<T>>
class Heap
{
public:explicit Heap(const Compare &cmp) : _con(), _cmp(cmp) {}Heap() : _con() {}void push(const T &x){_con.push_back(x);AdjustUp(_con.size() - 1);}void pop(){swap(_con[0], _con[_con.size() - 1]);_con.pop_back();AdjustDown(0);}T top() const{return _con[0];}bool empty() const{return _con.empty();}bool size() const{return _con.size();}private:void AdjustDown(int parent){int child = parent * 2 + 1;int n = _con.size();while (child < n){if (child + 1 < n && _cmp(_con[child], _con[child + 1])){child++;}if (_cmp(_con[parent], _con[child])){swap(_con[parent], _con[child]);parent = child;child = parent * 2 + 1;}elsebreak;}}void AdjustUp(int child){int parent = (child - 1) / 2;while (parent >= 0){if (_cmp(_con[parent], _con[child])){swap(_con[parent], _con[child]);child = parent;parent = (parent - 1) / 2;}elsebreak;}}private:Container _con;Compare _cmp;
};

![[OpenCV-dlib]人脸识别功能拓展-通过随机要求头部动作实现活体检测](http://pic.xiahunao.cn/[OpenCV-dlib]人脸识别功能拓展-通过随机要求头部动作实现活体检测)


方法)









需要在BIOS设置关闭热键功能可以这样操作!)
)



