1、 线性回归的原理
1.1 线性回归应用场景
房价预测
销售额度预测
金融:贷款额度预测、利用线性回归以及系数分析因子

1.2 什么是线性回归
1.2.1定义与公式
线性回归(Linear regression)是利用回归方程(函数)对一个或多个自变量(特征值)和因变量(目标值)之间关系进行建模的一种分析方式。
- 特点:只有一个自变量的情况称为单变量回归,大于一个自变量情况的叫做多元回归
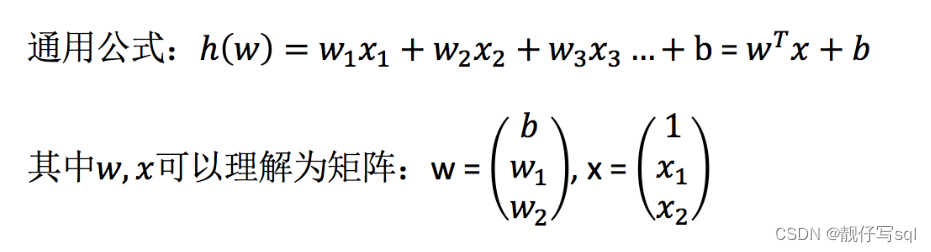
那么怎么理解呢?我们来看几个例子
期末成绩 = 0.7×考试成绩+0.3×平时成绩
房子价格 = 0.02×中心区域的距离 + 0.04×城市一氧化氮浓度 + (-0.12×自住房平均房价) + 0.254×城镇犯罪率
上面两个例子,我们看到特征值与目标值之间建立的一个关系,这个可以理解为回归方程。
1.2.2 线性回归的特征与目标的关系分析
线性回归当中的关系有两种,一种是线性关系,另一种是非线性关系。在这里我们只能画一个平面更好去理解,所以都用单个特征举例子。
- 线性关系
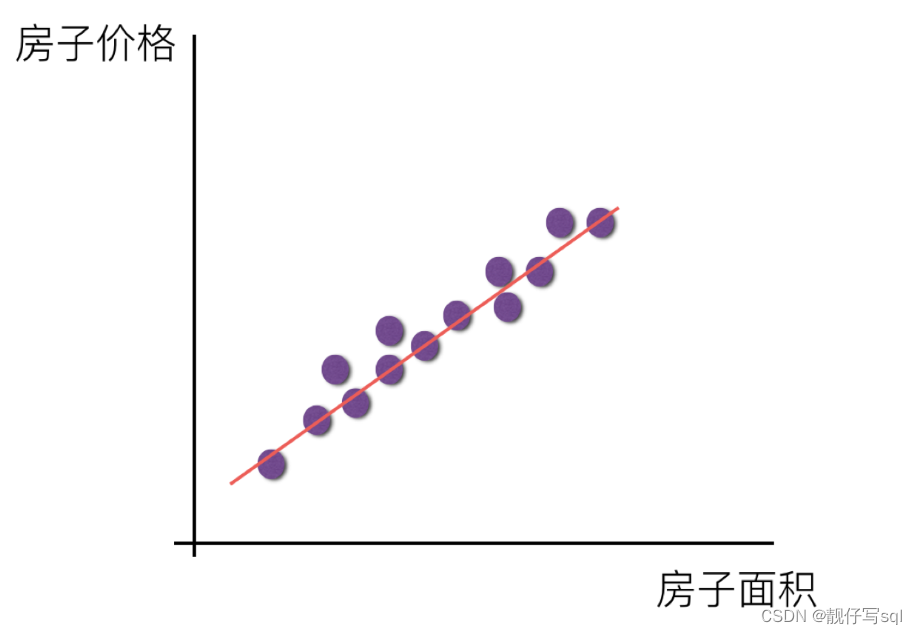
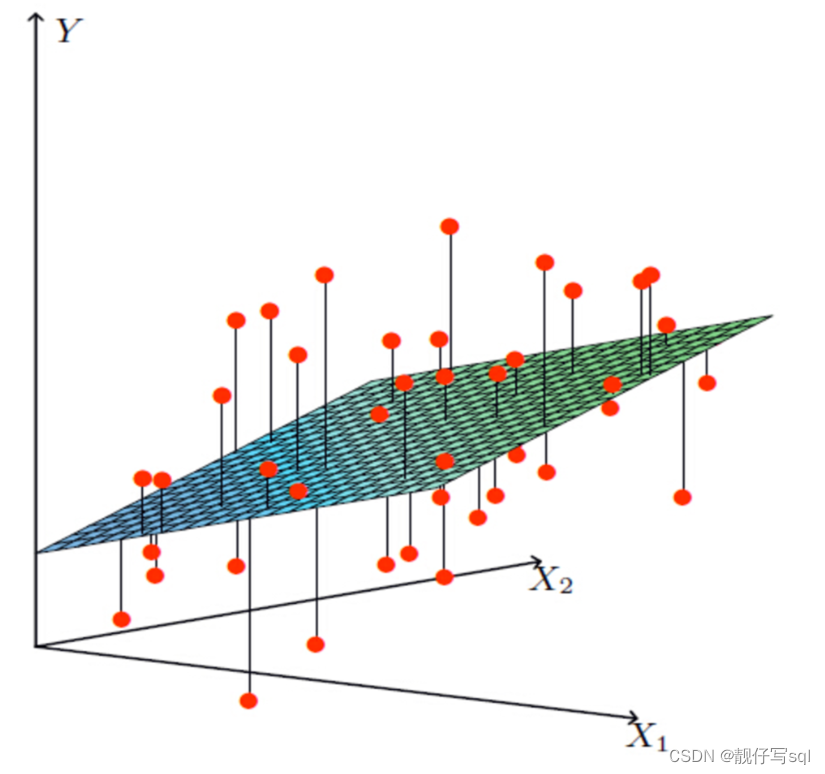
注释:如果在单特征与目标值的关系呈直线关系,或者两个特征与目标值呈现平面的关系
更高维度的我们不用自己去想,记住这种关系即可

注释:为什么会这样的关系呢?原因是什么?我们后面 讲解过拟合欠拟合重点介绍
如果是非线性关系,那么回归方程可以理解为:
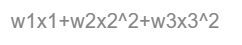
1.2.3 广义线性模型
非线性关系?
线性模型
1、自变量一次
y = w1x1 + w2x2 + w3x3 + …… + wnxn + b
2、参数一次
y = w1x1 + w2x1^2 + w3x1^3 + w4x2^3 + …… + b
1.2.4 线性关系&线性模型
1、线性关系一定是线性模型
2、线性模型不一定是线性关系
2、线性回归的损失函数和优化原理(理解记忆)
假设刚才的房子例子,真实的数据之间存在这样的关系
真实关系:真实房子价格 = 0.02×中心区域的距离 + 0.04×城市一氧化氮浓度 + (-0.12×自住房平均房价) + 0.254×城镇犯罪率
那么现在呢,我们随意指定一个关系(猜测)
随机指定关系:预测房子价格 = 0.25×中心区域的距离 + 0.14×城市一氧化氮浓度 + 0.42×自住房平均房价 + 0.34×城镇犯罪率
请问这样的话,会发生什么?真实结果与我们预测的结果之间是不是存在一定的误差呢?类似这样样子
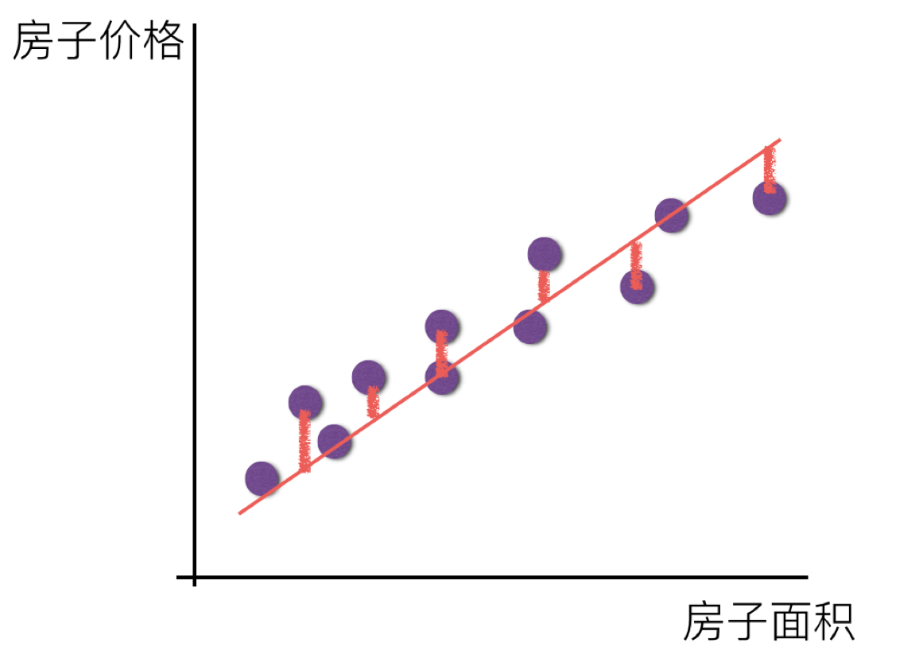
那么存在这个误差,我们将这个误差给衡量出来。
2.1 损失函数
总损失定义为:

如何去减少这个损失,使我们预测的更加准确些?既然存在了这个损失,我们一直说机器学习有自动学习的功能,在线性回归这里更是能够体现。这里可以通过一些优化方法去优化(其实是数学当中的求导功能)回归的总损失!!!
2.2 优化算法
如何去求模型当中的W,使得损失最小?(目的是找到最小损失对应的W值)
线性回归经常使用的两种优化算法
-
优化方法?
-
正规方程
- 天才 - 直接求解W
拓展:
1)求导,得到最大最小值:
y = ax^2 + bx + c
y’ = 2ax + b = 0
x = - b / 2a
2)矩阵逆计算:
a * b = 1
b = 1 / a = a ^ -1
A * B = E
[[1, 0, 0],
[0, 1, 0],
[0, 0, 1]]
B = A ^ -1
- 天才 - 直接求解W
-
梯度下降
勤奋努力的普通人
试错、改进
-
-
正规方程
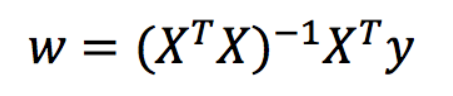
理解:X为特征值矩阵,y为目标值矩阵。直接求到最好的结果
缺点:当特征过多过复杂时,求解速度太慢并且得不到结果
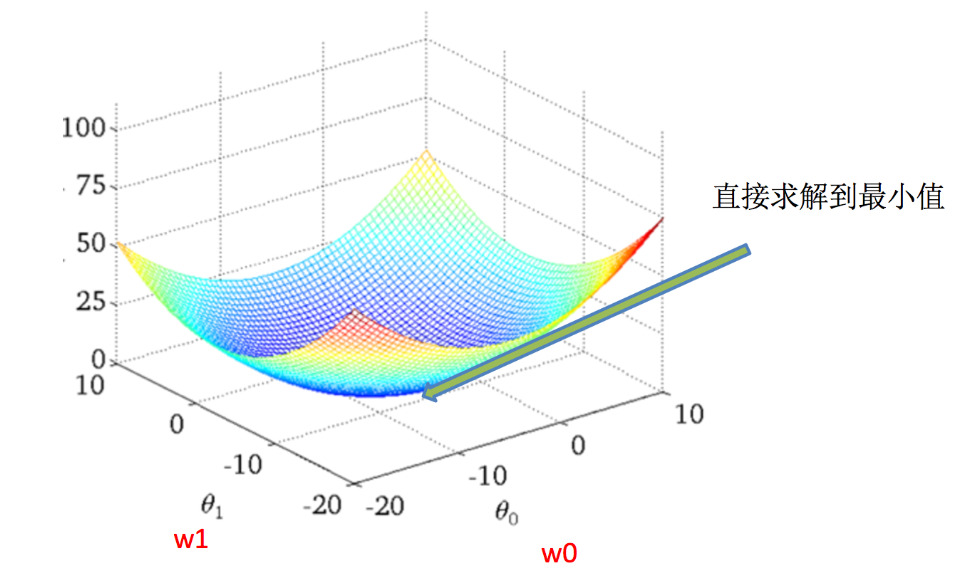
- 梯度下降(Gradient Descent)
公式:
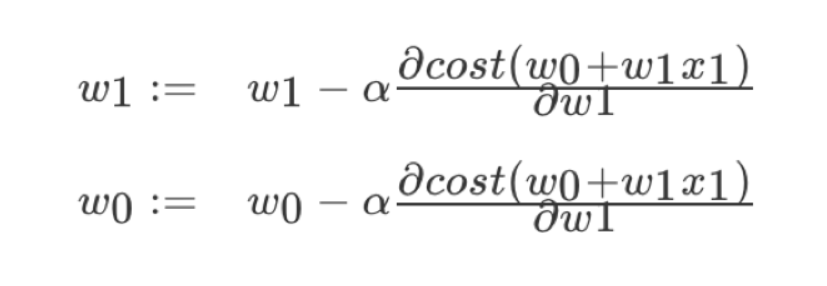
理解:α为学习速率,需要手动指定(超参数),α旁边的整体表示方向
沿着这个函数下降的方向找,最后就能找到山谷的最低点,然后更新W值
使用:面对训练数据规模十分庞大的任务 ,能够找到较好的结果
我们通过两个图更好理解梯度下降的过程
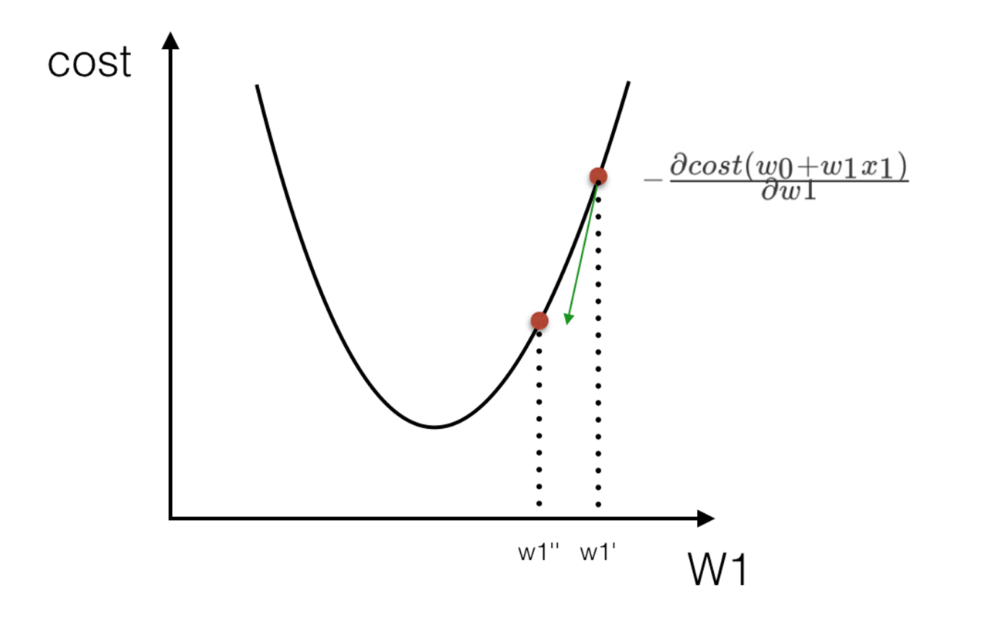
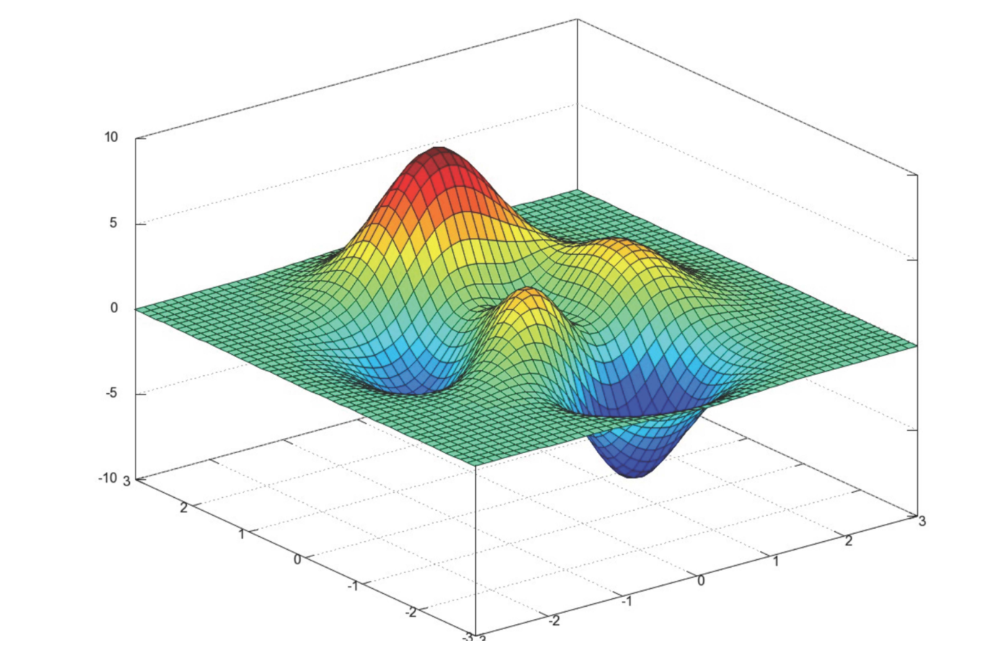
所以有了梯度下降这样一个优化算法,回归就有了"自动学习"的能力
3、 线性回归API
-
sklearn.linear_model.LinearRegression(fit_intercept=True) # 通过方程计算的最小二乘法实现系数的解析
- 通过正规方程优化
- fit_intercept:是否计算偏置
- LinearRegression.coef_:回归系数
- LinearRegression.intercept_:偏置
-
sklearn.linear_model.SGDRegressor(loss=“squared_loss”, fit_intercept=True, learning_rate =‘invscaling’, eta0=0.01)
- SGDRegressor类实现了随机梯度下降学习,它支持不同的loss函数和正则化惩罚项来拟合线性回归模型。
- loss:损失类型
- loss=”squared_loss”: 普通最小二乘法
- fit_intercept
- 是否计算偏置
- learning_rate : string, optional 学习率算法
- ‘constant’(常数): eta = eta0 (eta0 :初始学习率)
- ‘optimal’: eta = 1.0 / (alpha * (t + t0)) [default]
- ‘invscaling’: eta = eta0 / pow(t, power_t)
- power_t=0.25:存在父类当中,对于一个常数值的学习率来说,可以使用learning_rate=’constant’ ,并使用eta0来指定学习率。
- SGDRegressor.coef_:回归系数
- SGDRegressor.intercept_:偏置
4、波士顿房价预测
4.1 分析开发流程:
- 获取数据集
- 划分数据集
- 特征工程:无量纲化 - 标准化
- 预估器流程:fit() --> 模型, coef_ intercept_
- 模型评估:
- 回归的性能评估:均方误差
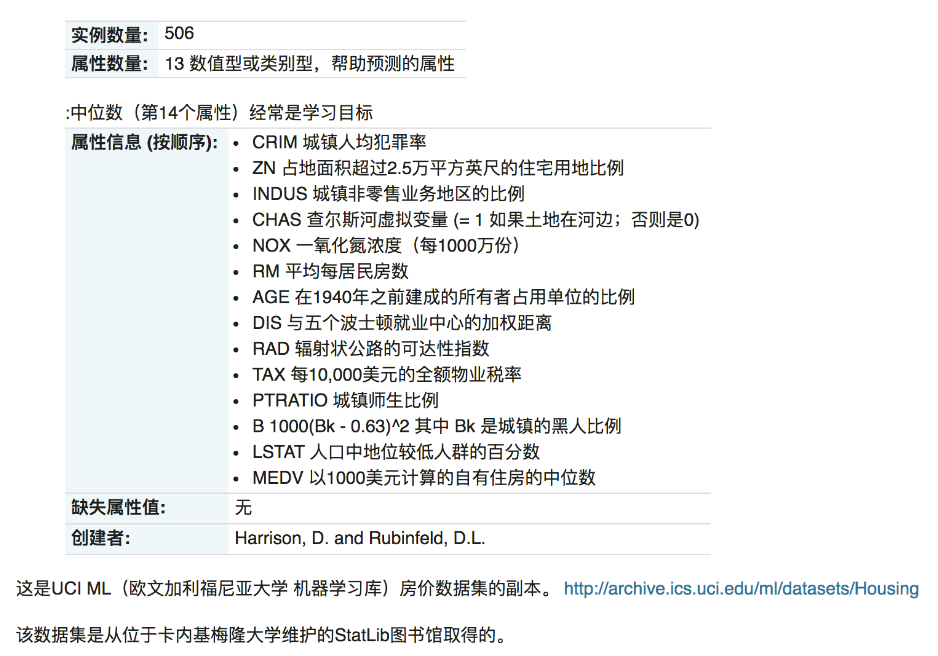
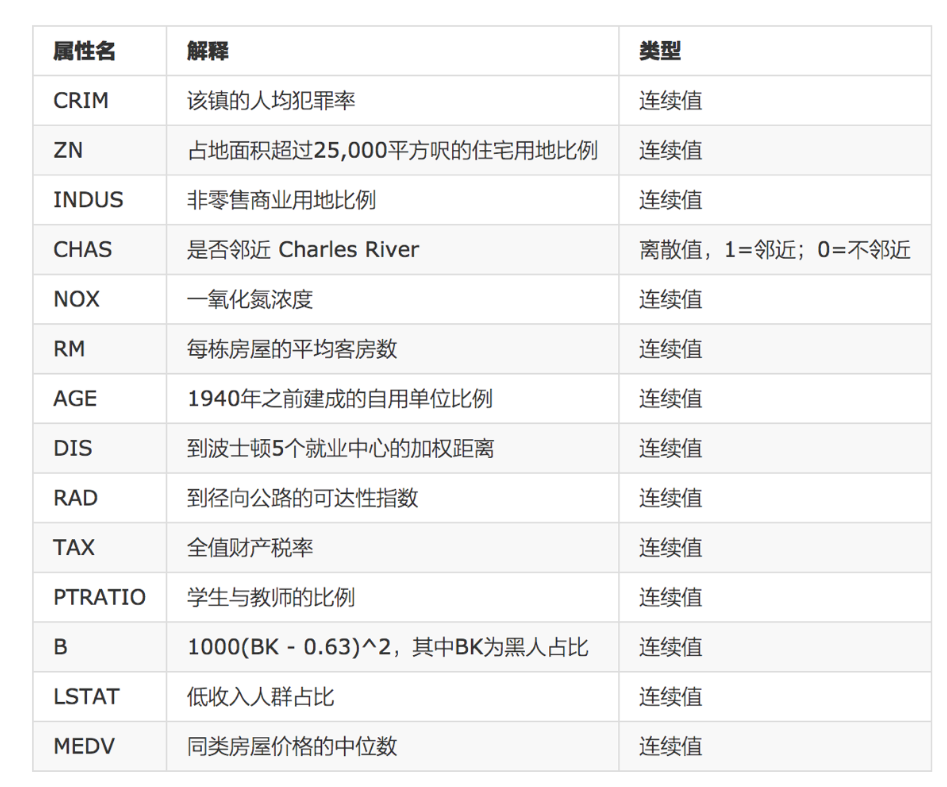
- 数据介绍
4.2 分析
回归当中的数据大小不一致,是否会导致结果影响较大。所以需要做标准化处理。同时我们对目标值也需要做标准化处理。
- 数据分割与标准化处理
- 回归预测
- 线性回归的算法效果评估
4.3 回归性能评估
均方误差(Mean Squared Error)MSE)评价机制:
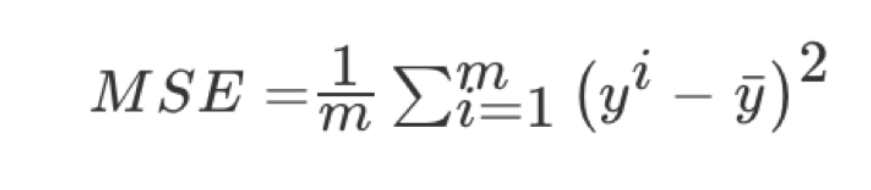
注:y^i为预测值,¯y为真实值
- sklearn.metrics.mean_squared_error(y_true, y_pred)
- 均方误差回归损失
- y_true:真实值
- y_pred:预测值
- return:浮点数结果
4.4正规方程和梯度下降对比
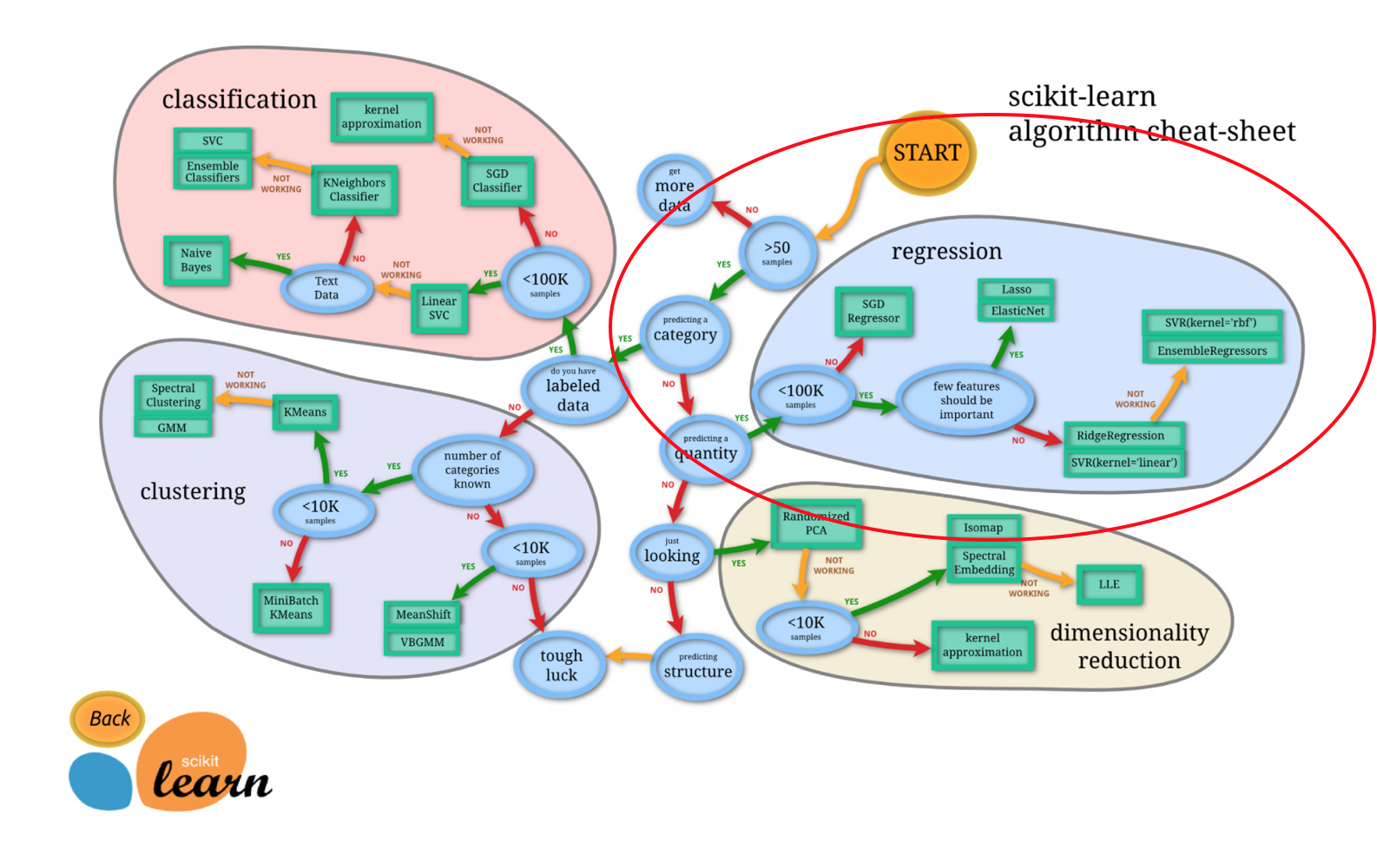
如图红色圈圈显示,官方给出的使用api的意见。
- 文字对比
| 梯度下降 | 正规方程 |
|---|---|
| 需要选择学习率 | 不需要 |
| 需要迭代求解 | 一次运算得出 |
| 特征数量较大可以使用 | 需要计算方程,时间复杂度高O(n3) |
- 选择:
- 小规模数据:
- LinearRegression(不能解决欠或过拟合问题)
- 岭回归,LASSO(可解决拟合问题)
- 大规模数据:
- SGDRegressor
4.5 完整代码
import pandas as pd
from sklearn.linear_model import LinearRegression, SGDRegressor
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
import numpy as npdata_url = "http://lib.stat.cmu.edu/datasets/boston"
raw_df = pd.read_csv(data_url, sep="\s+", skiprows=22, header=None)
data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
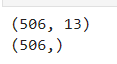
target = raw_df.values[1::2, 2]print(data.shape)
print(target.shape)
print("data:\n",data)
print("target:\n",target)

x_train, x_test, y_train, y_test = train_test_split(data, target, test_size=0.3, random_state=24)
print(x_train.shape)
print(x_test.shape)
print(y_train.shape)
print(y_test.shape)
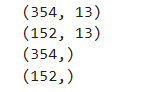
print(x_train)
print(x_test)
print(y_train)
print(y_test)


from sklearn.preprocessing import StandardScaler
# 需要做标准化处理对于特征值处理
std_x = StandardScaler()
x_train = std_x.fit_transform(x_train)
x_test = std_x.fit_transform(x_test)
print("x_train:\n", x_train)
print("x_test:\n", x_test)

# 使用线性模型进行预测
# 使用正规方程求解
lr = LinearRegression()
# # 此时在干什么?
lr.fit(x_train, y_train)
y_lr_predict = lr.predict(x_test)
print(lr.coef_)
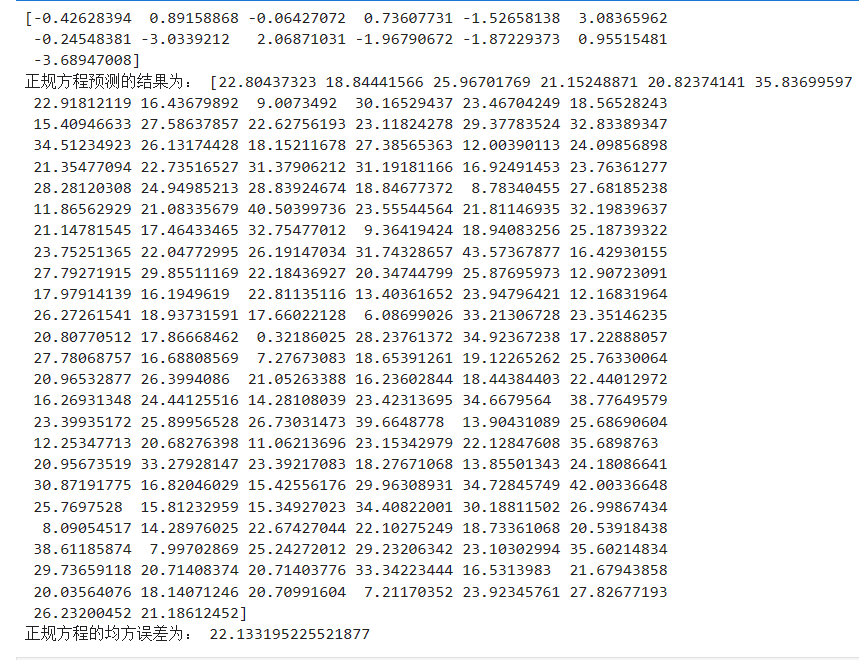
print("正规方程预测的结果为:", y_lr_predict)
print("正规方程的均方误差为:", mean_squared_error(y_test, y_lr_predict))
# 随机梯度下降进行预测
# 随机梯度下降进行预测
sgd = SGDRegressor(learning_rate ='optimal', eta0=0.01, alpha=0.01, max_iter=1000)sgd.fit(x_train, y_train)
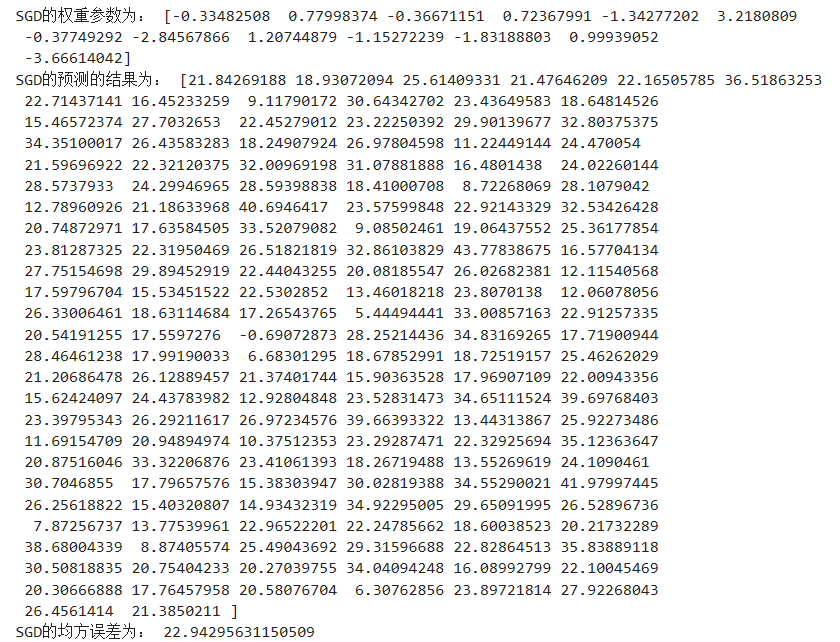
print("SGD的权重参数为:", sgd.coef_)
y_sgd_predict = sgd.predict(x_test)
print("SGD的预测的结果为:", y_sgd_predict)
# # 怎么评判这两个方法好坏
print("SGD的均方误差为:", mean_squared_error(y_test, y_sgd_predict))
5、拓展-关于优化方法GD、SGD、SAG
5.1 GD
梯度下降(Gradient Descent),原始的梯度下降法需要计算所有样本的值才能够得出梯度,计算量大,所以后面才有会一系列的改进。
5.2 SGD
随机梯度下降(Stochastic gradient descent)是一个优化方法。它在一次迭代时只考虑一个训练样本。
SGD的优点是:
高效
容易实现
SGD的缺点是:
SGD需要许多超参数:比如正则项参数、迭代数。
SGD对于特征标准化是敏感的。
5.3 SAG
随机平均梯度法(Stochasitc Average Gradient),由于收敛的速度太慢,有人提出SAG等基于梯度下降的算法
Scikit-learn:SGDRegressor、岭回归、逻辑回归等当中都会有SAG优化
死循环的问题)


















)