题目描述
这是 LeetCode 上的 「109. 有序链表转换二叉搜索树」 ,难度为 「中等」
Tag : 「二叉树」、「树的搜索」、「分治」、「中序遍历」
给定一个单链表的头节点 head,其中的元素 按升序排序 ,将其转换为高度平衡的二叉搜索树。
本题中,一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差不超过 。
示例 1: 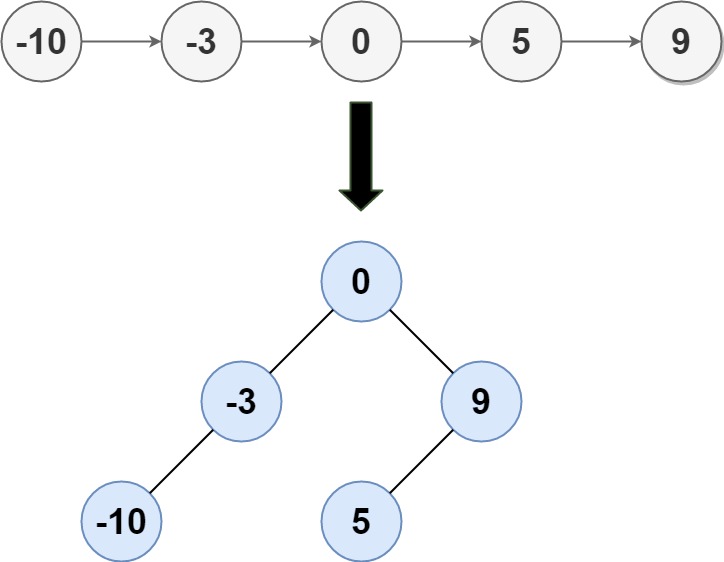
输入: head = [-10,-3,0,5,9]
输出: [0,-3,9,-10,null,5]
解释: 一个可能的答案是[0,-3,9,-10,null,5],它表示所示的高度平衡的二叉搜索树。
示例 2:
输入: head = []
输出: []
提示:
-
head中的节点数在 范围内 -
递归分治
与上一题 108. 将有序数组转换为二叉搜索树 类似,但链表相对于数组,无法 找到构建当前 BST 根节点的“中点”下标。
一个仍可确保 时间复杂度(瓶颈在于需要创建 个节点),但需要 空间复杂度的做法是:对链表进行一次遍历,转成数组后套用上一题的做法。
一个不使用 空间复杂度的做法,需要每次遍历来找“中点”下标:起始我们先对 head 进行一次遍历,得到链表长度 ,随后仍然利用递归分治的思路进行构造,每次对入参的左右端点找“中点”,先通过直接结算的方式定位到偏移量 ,然后再通过从入参节点 head 出发往前走 的做法找到“中点”节点。
该做法每个节点的访问次数为在递归过程中被 所覆盖的次数,我们知道一个节点数量为 的平衡 BST 树高为 ,因此整体复杂度为 。
Java 代码:
class Solution {
public TreeNode sortedListToBST(ListNode head) {
int n = 0;
ListNode cur = head;
while (cur != null && ++n >= 0) cur = cur.next;
return build(head, 0, n - 1);
}
TreeNode build(ListNode head, int l, int r) {
if (l > r) return null;
int mid = l + r >> 1, t = mid - l;
ListNode cur = head;
while (t-- > 0) cur = cur.next;
TreeNode ans = new TreeNode(cur.val);
ans.left = build(head, l, mid - 1);
ans.right = build(cur.next, mid + 1, r);
return ans;
}
}
Python 代码:
class Solution:
def sortedListToBST(self, head: Optional[ListNode]) -> Optional[TreeNode]:
n = 0
cur = head
while cur:
n += 1
cur = cur.next
return self.build(head, 0, n - 1)
def build(self, head: ListNode, l: int, r: int) -> TreeNode:
if l > r:
return None
mid = l + r >> 1
t = mid - l
cur = head
while t > 0:
cur = cur.next
t -= 1
ans = TreeNode(cur.val)
ans.left = self.build(head, l, mid - 1)
ans.right = self.build(cur.next, mid + 1, r)
return ans
C++ 代码:
class Solution {
public:
TreeNode* sortedListToBST(ListNode* head) {
int n = 0;
ListNode* cur = head;
while (cur && ++n >= 0) cur = cur->next;
return build(head, 0, n - 1);
}
TreeNode* build(ListNode* head, int l, int r) {
if (l > r) return nullptr;
int mid = l + r >> 1, t = mid - l;
ListNode* cur = head;
while (t-- > 0) cur = cur->next;
TreeNode* ans = new TreeNode(cur->val);
ans->left = build(head, l, mid - 1);
ans->right = build(cur->next, mid + 1, r);
return ans;
}
};
TypeScript 代码:
function sortedListToBST(head: ListNode | null): TreeNode | null {
const build = function (head: ListNode | null, l: number, r: number): TreeNode | null {
if (l > r) return null;
let mid = l + r >> 1, t = mid - l;
let cur = head;
while (t-- > 0) cur = cur.next;
const ans = new TreeNode(cur!.val);
ans.left = build(head, l, mid - 1);
ans.right = build(cur!.next, mid + 1, r);
return ans;
}
let n = 0;
let cur = head;
while (cur != null && ++n >= 0) cur = cur.next;
return build(head, 0, n - 1);
}
-
时间复杂度: -
空间复杂度:
递归分治 - 中序遍历
由于给定的 nums 本身严格有序,而 BST 的中序遍历亦是有序。因此我们可以一边遍历链表,一边对 BST 进行构造。
具体的,我们仍然先对链表进行遍历,拿到链表长度 n。递归构造过程中传入左右端点 l 和 r,含义为使用链表中 部分节点,但不再在每次递归中传入当前头结点,而是使用全局变量 head 来记录。
递归构造过程中,计算“中点”位置 ,并根据如下流程进行构造:
-
使用 构建左子树,使用变量 left保存当前左子树的根节点 -
构建完左子树后,全局变量 head必然来到了“中点”位置,用其构建根节点ans,并将根节点与此前构造的left关联。同时让链表节点head后移 -
使用 构建右子树,并将其挂载到根节点 ans中
如此一来,即可确保「链表遍历」和「BST 构造」的同步性。
Java 代码:
class Solution {
ListNode head;
public TreeNode sortedListToBST(ListNode _head) {
head = _head;
int n = 0;
ListNode cur = head;
while (cur != null && ++n >= 0) cur = cur.next;
return build(0, n - 1);
}
TreeNode build(int l, int r) {
if (l > r) return null;
int mid = l + r >> 1;
TreeNode left = build(l, mid - 1);
TreeNode ans = new TreeNode(head.val);
head = head.next;
ans.left = left;
ans.right = build(mid + 1, r);
return ans;
}
}
Python 代码:
class Solution:
def sortedListToBST(self, head: Optional[ListNode]) -> Optional[TreeNode]:
self.head = head
n = 0
cur = self.head
while cur is not None:
n += 1
cur = cur.next
return self.build(0, n - 1)
def build(self, l: int, r: int) -> TreeNode:
if l > r:
return None
mid = l + r >> 1
left = self.build(l, mid - 1)
ans = TreeNode(self.head.val)
ans.left = left
self.head = self.head.next
ans.right = self.build(mid + 1, r)
return ans
C++ 代码:
class Solution {
public:
ListNode* head;
TreeNode* sortedListToBST(ListNode* _head) {
head = _head;
int n = 0;
ListNode* cur = head;
while (cur && n++ >= 0) cur = cur->next;
return build(0, n - 1);
}
TreeNode* build(int l, int r) {
if (l > r) return nullptr;
int mid = l + r >> 1;
TreeNode* left = build(l, mid - 1);
TreeNode* ans = new TreeNode(head->val);
ans->left = left;
head = head->next;
ans->right = build(mid + 1, r);
return ans;
}
};
TypeScript 代码:
function sortedListToBST(_head: ListNode | null): TreeNode | null {
const build =function(l: number, r: number): TreeNode | null {
if (l > r) return null;
const mid = l + r >> 1;
const left = build(l, mid - 1);
const ans = new TreeNode(head.val);
ans.left = left;
head = head.next;
ans.right = build(mid + 1, r);
return ans;
}
let head = _head;
let n = 0, cur = head;
while (cur && n++ >= 0) cur = cur.next;
return build(0, n - 1);
}
-
时间复杂度: -
空间复杂度:
最后
这是我们「刷穿 LeetCode」系列文章的第 No.109 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSource/LogicStack-LeetCode 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
更多更全更热门的「笔试/面试」相关资料可访问排版精美的 合集新基地 🎉🎉
本文由 mdnice 多平台发布
)
详细设计中面向对象方法下的模块化)




解决)



——事务与存储引擎)








)