目录
前言
1.什么是红黑树?
2.为什么需要红黑树?(与AVL树对比)
3.红黑树的特性
前言
在此之前我们学习过了二叉排序树和平衡二叉树(AVL树),这两种树都是属于搜索树的一种,那么今天我们就开始学习一种新的搜索树,即红黑树,可能在接触二叉树学习的时候我们就听说过了红黑树,当然我们也知道,红黑树相较于前面所学的数据结构(链表、栈、队列、堆……)都难上了很多倍,那么这一期我就来初步的介绍红黑树的相关特性和其知识点,后面我会详细发布关于红黑树的文章来进一步介绍红黑树的操作和代码实现,废话不多说,开始今天的学习吧!
相关链接:
二叉排序树:数据结构-----二叉排序树_Gretel Tade的博客-CSDN博客
AVL树:数据结构-----平衡二叉树_Gretel Tade的博客-CSDN博客
1.什么是红黑树?
红黑树是一种自平衡的二叉查找树,是一种高效的查找树。它是由 Rudolf Bayer 于1972年发明,在当时被称为对称二叉 B 树(symmetric binary B-trees)。后来,在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的红黑树。
红黑树如图所示: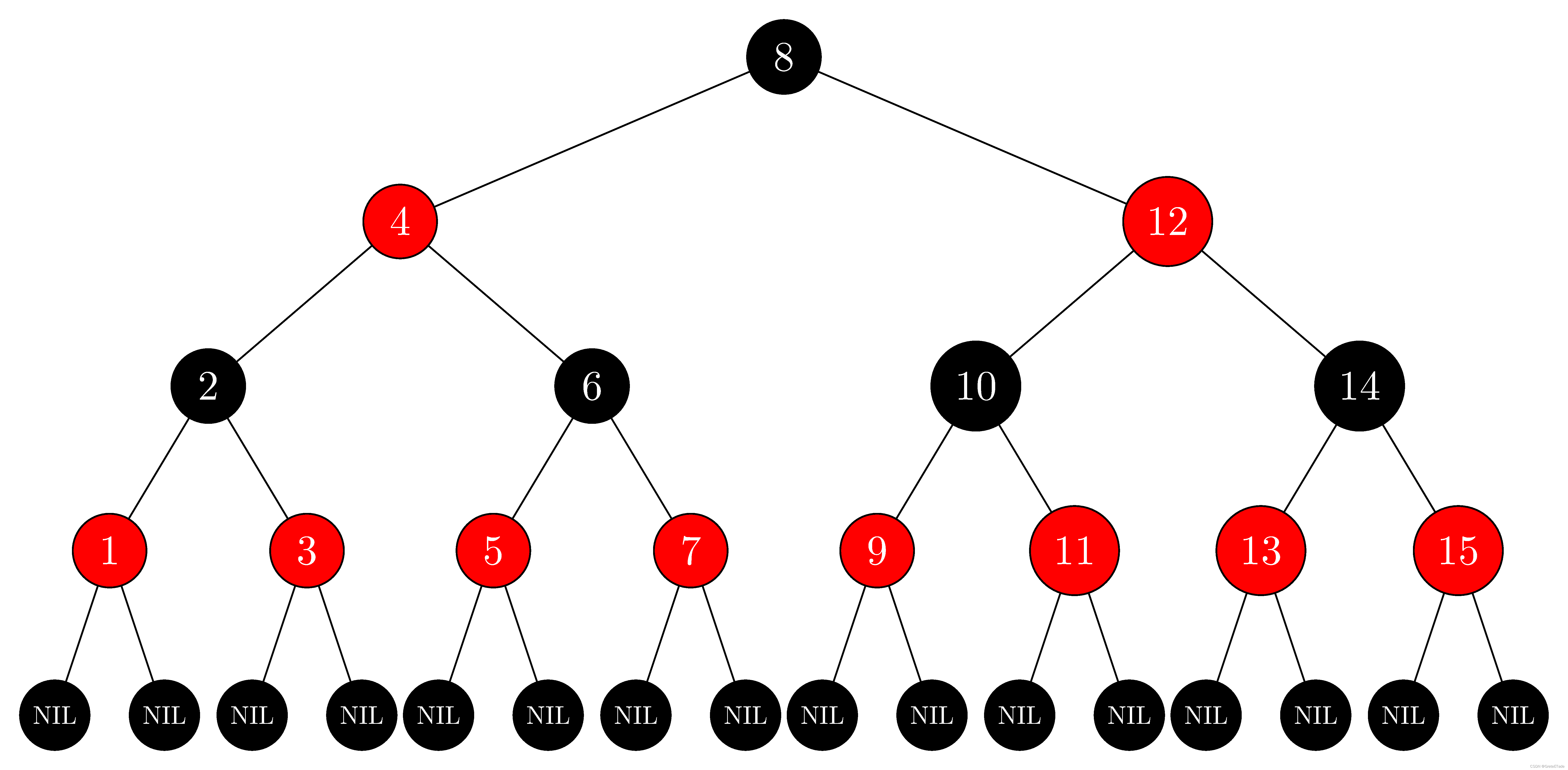
2.为什么需要红黑树?(与AVL树对比)
在此之前我们学习了AVL树,既然AVL树有了高效率的查找功能,那需要红黑树干什么呢?下面看对比就知道了。
红黑树(Red-Black Tree)和AVL树(Adelson-Velsky and Landis Tree)都是自平衡二叉搜索树,用于在动态数据集上进行高效的插入、删除和搜索操作。它们之间有一些相似之处,但也存在一些关键的区别。如下所示:
平衡性比较:
AVL树:平衡二叉树是一种绝对平衡的二叉树,其满足每个节点的左右子树的高度只差不超过1,所以其在查找方面上是非常迅捷的,但是在插入和删除操作的时候要不断去旋转来满足平衡条件。
红黑树:红黑树是一种弱平衡的二叉树,其不需要像AVL树那样满足左右子树高度差不超过1,红黑树树的高度最多是2倍的对数级别,所以红黑树的插入和删除操作方面更具有灵活性,但是有一些方面性能还是不如AVL树的。
插入和删除性能比较:
AVL树:AVL树在插入和删除过程中必须满足绝对平衡,所以要频繁的进行旋转操作,时间复杂度比较大
红黑树:红黑树是满足弱平衡状态,有红黑两种颜色去控制树的结构,在插入和删除过程中不需要多次旋转操作,这方面是优于平衡二叉树的。
操作效率比较:
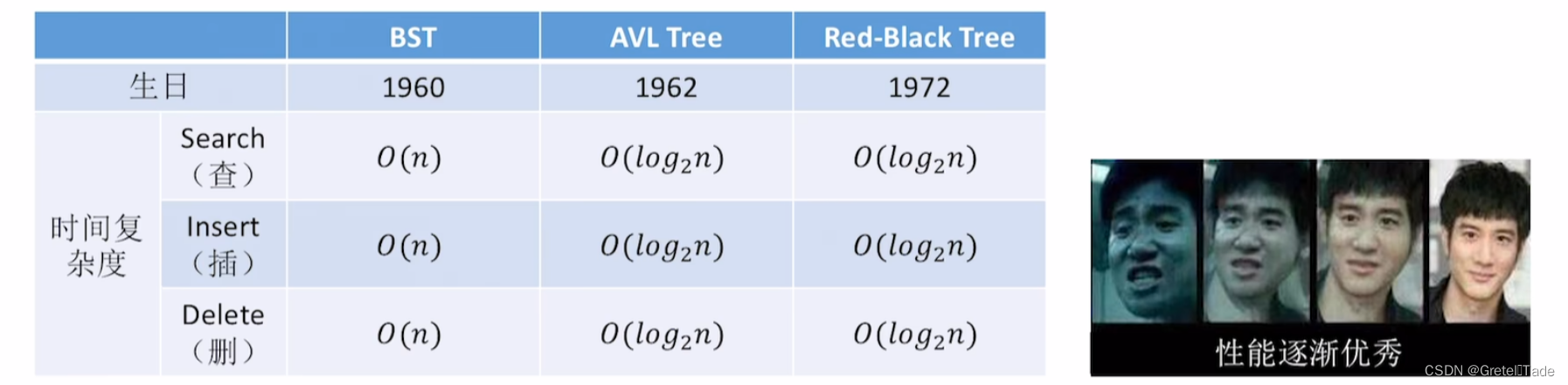
AVL树:平衡二叉树满足绝对平衡,其查找效率绝对是最快的,时间复杂度为 O(logn).
红黑树:虽然红黑树的查找时间复杂度也是O(logn),但是相较于平衡二叉树,操作速度是要慢一些的。

对比总结
AVL树:适合应用于搜索场景,以查为主。
红黑树:适合用于频繁插入、删除场景,其实用性更加强。
总的来说各有各的特色吧,现实生活和工作中用的比较多的方面那肯定是红黑树的了,所以学好红黑树很重要!!!
红黑树的相关应用场景:
红黑树具有良好的效率,它可在 O(logN) 时间内完成查找、增加、删除等操作。因此,红黑树在业界应用很广泛,比如 Java 中的 TreeMap,JDK 1.8 中的 HashMap、C++ STL 中的 map 均是基于红黑树结构实现的。
3.红黑树的特性
既然知道了红黑树的优秀,多余的就不多说了,所以这里就开始学习红黑树的知识点了,首先先了解红黑树的特性,需要什么条件才可以满足红黑树。
对于一个红黑树必须满足以下的6个特性:
1.红黑树是一个二叉排序树
2.每个节点要么是红色,要么是黑色
3.根结点是黑色的
4.叶子节点(外部节点,NULL节点、失败的节点)都是黑色的
5.红色节点的父节点和子节点都是黑色的(不存在两个相邻的红色节点)
6.对于每一个节点,从该节点到任一叶子结点的路径上,其所含黑色节点的数量相同
红黑树上面这6条性质可能对于有些人不太好记住或者记错,别急,我下面送各位一个顺口溜,保证你们看了就懂:

顺口溜解释:
左根右:表示红黑树满足 左子节点<根节点<右子节点,也就是满足排序条件
根叶黑:表示跟节点和叶子节点都是黑色的
不红红:表示不能有两个连续的红色节点(父节点和子节点不可能同时是红色的)
黑路同:表示从任意应该节点走到子节点路径上的黑色节点数量是相同的
记住了这个顺口溜就等于记住了红黑树的特性,是不是很简单呢?来下面看几个简单的判断是否为红黑树的示例:
示例1:
很明显这个不是红黑树,为什么呢?没有排序啊!!!
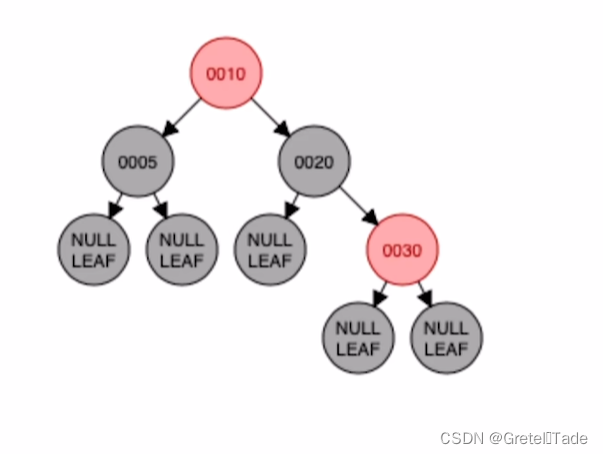
示例2:
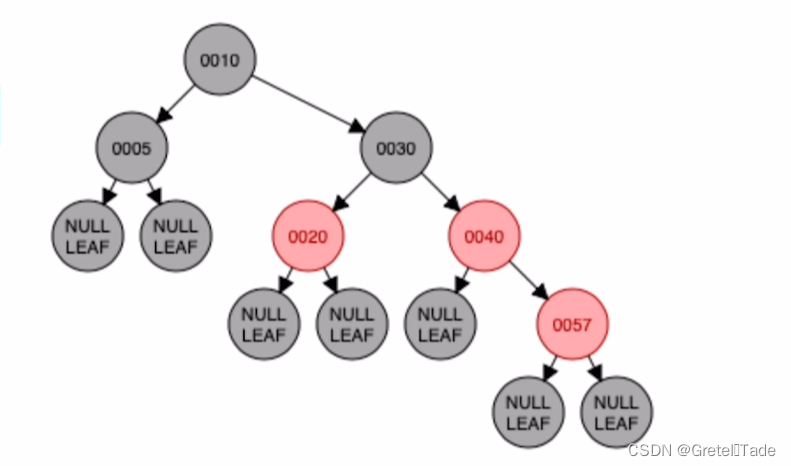
这个也不是红黑树,因为不满足 “不红红” 的特性。
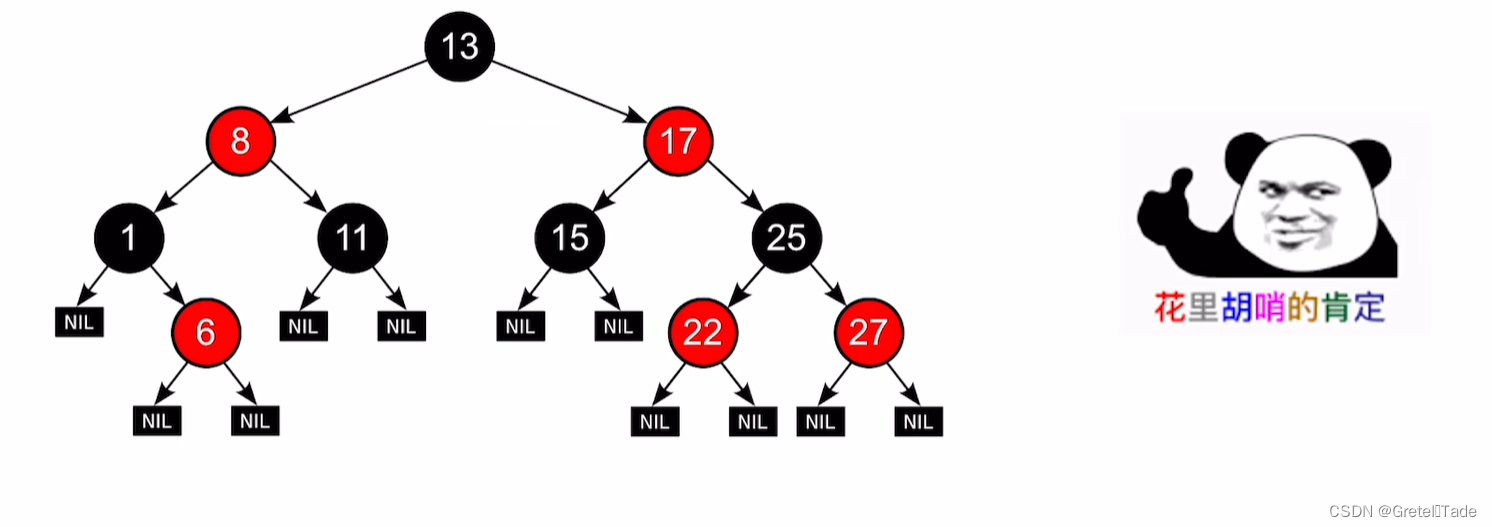
示例3: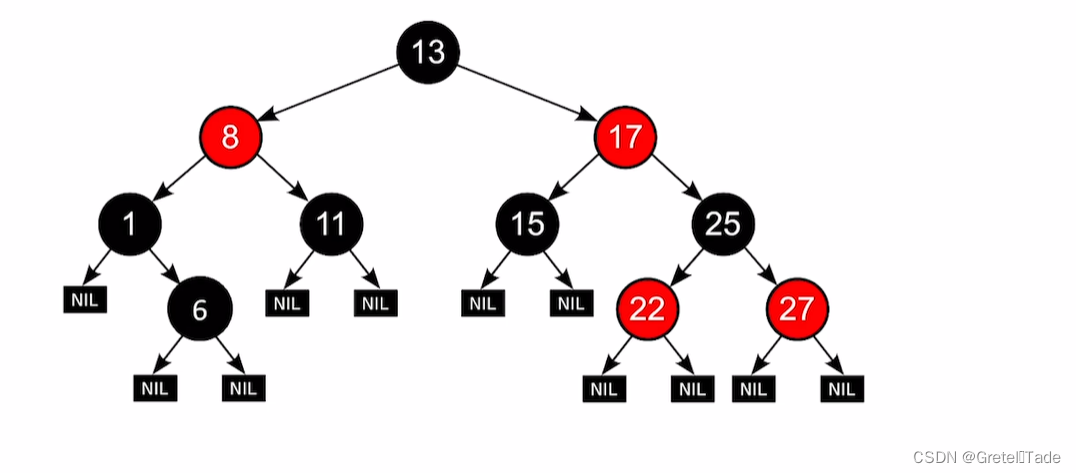
这个也不是红黑树,可能有点不太好看,看到13->8->1->6 这条路径,发现有什么不同呢?很明显,这里不满足 “黑路同” 的性质,相较于其他路径这里多了一个黑色节点的数量。
这一期就先介绍到这里,先初步认识一下红黑树,下一期我们就正式开始进入到了红黑树的深入学习,包括节点的插入和删除等操作,我们下次见咯!
分享一张壁纸:

)




)



)

】:存在重复元素)






:自动化跨区域中心数据分发)