进化算法------微生物进化算法（MGA）

前言

该文章写在GA算法之后：GA算法

遗传算法 (GA)的问题在于没有有效保留好的父母 (Elitism), 让好的父母不会消失掉. Microbial GA (后面统称 MGA) 就是一个很好的保留 Elitism 的算法.

一句话来概括: 在袋子里抽两个球, 对比两个球, 把球大的放回袋子里, 把球小的变一下再放回袋子里, 这样在这次选着中,
大球不会被改变任何东西, 就被放回了袋子, 当作下一代的一部分.

算法思想

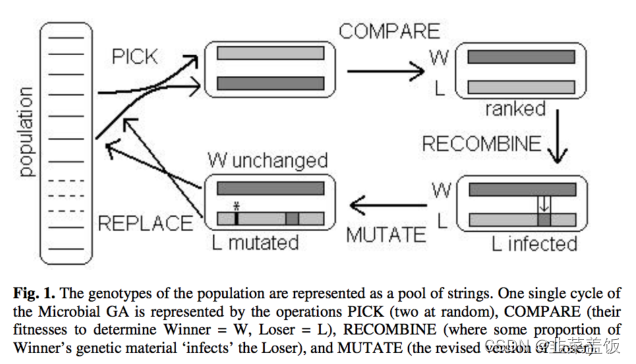
在这里插入图片描述
每次在进化的时候, 我们会从这个 pop 中随机抽 2 个 DNA 出来, 然后对比一下他们的 fitness, 我们将 fitness 高的定义成 winner, 反之是 loser. 我们不会去动任何 winner 的 DNA, 我们只对 loser, 比如对 loser 的DNA进行修改，进行 crossover 和 mutate. 之后将 winner 和 loser 一同放回 pop 中.

通过这样的流程, 我们就不用担心有时候变异着变异着, 那些原本好的 pop 流失掉了, 有了这个 MGA 算法, winner 总是会被保留下来的. GA 中的 Elitism 问题通过这种方法巧妙解决了.

示例

我们以曲线寻找最大值为例子
在这里插入图片描述

本算法与GA算法的区别在于交叉时，我们将选择的两个个体，一个winner一个loser，我们将winner的部分DNA复制给loser
代码如下：

 def crossover(self, loser_winner):  # mating process (genes crossover)"""交叉配对:param parent::param pop::return:"""# 生成一个长度DNA_size的布尔类型的数组  布尔值来选择相应的交叉点进行交叉操cross_idx = np.empty((self.DNA_size,)).astype(np.bool_)for i in range(self.DNA_size):cross_idx[i] = True if np.random.rand() < self.cross_rate else False# 将winner的DNA和loser的DNA交叉，重新赋值给loserloser_winner[0, cross_idx] = loser_winner[1, cross_idx]return loser_winner

其次是变异操作，我们进行交叉操作之后，我们对loser的DNA进行变异操作
代码如下：

 def mutate(self, loser_winner):"""变异操作:param loser_winner::return:"""# 生成要变异的结点mutation_idx = np.empty((self.DNA_size,)).astype(np.bool_)for i in range(self.DNA_size):mutation_idx[i] = True if np.random.rand() < self.mutate_rate else False  # mutation index# 进行变异loser_winner[0, mutation_idx] = ~loser_winner[0, mutation_idx].astype(np.bool_)return loser_winner

最后就是算法核心，GA算法是对种群进行select，而我们的MGA算法就是选择多次的loser和winner，这样适应度好的个体会一直保留在种群当中，而不会被替代
代码如下：

    def evolve(self, n):"""微生物进化算法:param n::return:"""# 从种群中取n次的 loser_winnerfor _ in range(n):# 获取两个个体的下标sub_pop_idx = np.random.choice(np.arange(0, self.pop_size), size=2, replace=False)# 得到两个个体sub_pop = self.pop[sub_pop_idx]# 获取适应度product = F(self.translateDNA(sub_pop))fitness = self.get_fitness(product)# 根据适应度对两个个体进行排序，适应度低的在第一个即loserloser_winner_idx = np.argsort(fitness)   #返回排序后的索引loser_winner = sub_pop[loser_winner_idx]  # the first is loser and second is winnerloser_winner = self.crossover(loser_winner)loser_winner = self.mutate(loser_winner)self.pop[sub_pop_idx] = loser_winnerDNA_prod = self.translateDNA(self.pop) # y轴pred = F(DNA_prod)   # x轴return DNA_prod, pred

完整代码如下

#!/usr/bin/env python 
# -*- coding:utf-8 -*-
import timeimport numpy as np
import matplotlib.pyplot as pltDNA_SIZE = 10            # DNA length  DNA长度
POP_SIZE = 20           # population size  种群大小
CROSS_RATE = 0.6         # mating probability (DNA crossover)  交叉配对的概率
MUTATION_RATE = 0.01    # mutation probability  编译的概率
N_GENERATIONS = 200     #   代数
X_BOUND = [0, 5]         # x upper and lower bounds   x轴范围def F(x):"""定义一个函数，就是图像中的线条:param x::return:"""return np.sin(10*x)*x + np.cos(2*x)*x     # to find the maximum of this functionclass MGA():def __init__(self, DNA_size, DNA_bound, cross_rate, mutation_rate, pop_size):self.DNA_size = DNA_sizeDNA_bound[1] += 1self.DNA_bound = DNA_boundself.cross_rate = cross_rateself.mutate_rate = mutation_rateself.pop_size = pop_size# initialize the pop DNA   s生成0-1的POP_SIZE行 DNA_SIZE列的种群self.pop = np.random.randint(2, size=(POP_SIZE, DNA_SIZE))def get_fitness(self,pred):"""获取个体的适用度:param pred::return:"""return pred + 1e-3 - np.min(pred)  # 防止适应度为负数def translateDNA(self,pop):"""将0 1 DNA序列翻译成范围在(0, 5)的数字:param pop::return:"""return pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * X_BOUND[1]def crossover(self, loser_winner):  # mating process (genes crossover)"""交叉配对:param parent::param pop::return:"""# 生成一个长度DNA_size的布尔类型的数组  布尔值来选择相应的交叉点进行交叉操cross_idx = np.empty((self.DNA_size,)).astype(np.bool_)for i in range(self.DNA_size):cross_idx[i] = True if np.random.rand() < self.cross_rate else False# 将winner的DNA和loser的DNA交叉，重新赋值给loserloser_winner[0, cross_idx] = loser_winner[1, cross_idx]return loser_winnerdef mutate(self, loser_winner):"""变异操作:param loser_winner::return:"""# 生成要变异的结点mutation_idx = np.empty((self.DNA_size,)).astype(np.bool_)for i in range(self.DNA_size):mutation_idx[i] = True if np.random.rand() < self.mutate_rate else False  # mutation index# 进行变异loser_winner[0, mutation_idx] = ~loser_winner[0, mutation_idx].astype(np.bool_)return loser_winnerdef evolve(self, n):"""微生物进化算法:param n::return:"""# 从种群中取n次的 loser_winnerfor _ in range(n):# 获取两个个体的下标sub_pop_idx = np.random.choice(np.arange(0, self.pop_size), size=2, replace=False)# 得到两个个体sub_pop = self.pop[sub_pop_idx]# 获取适应度product = F(self.translateDNA(sub_pop))fitness = self.get_fitness(product)# 根据适应度对两个个体进行排序，适应度低的在第一个即loserloser_winner_idx = np.argsort(fitness)   #返回排序后的索引loser_winner = sub_pop[loser_winner_idx]  # the first is loser and second is winnerloser_winner = self.crossover(loser_winner)loser_winner = self.mutate(loser_winner)self.pop[sub_pop_idx] = loser_winnerDNA_prod = self.translateDNA(self.pop) # y轴pred = F(DNA_prod)   # x轴return DNA_prod, predif __name__ == '__main__':plt.ion()  # something about plotting# x轴x = np.linspace(*X_BOUND, 200)plt.plot(x, F(x))# 初始化算法ga = MGA(DNA_size=DNA_SIZE, DNA_bound=[0, 1], cross_rate=CROSS_RATE, mutation_rate=MUTATION_RATE, pop_size=POP_SIZE)# 迭代N_GENERATIONS次for _ in range(N_GENERATIONS):# 进行进化算法DNA_prod, pred = ga.evolve(5)# 得到图像上的y值F_values = F(ga.translateDNA(ga.pop))# 获取每一个个体的适应度fitness = ga.get_fitness(F_values)# 获取最好适用度的个体下标i = np.argmax(fitness)print("最优DNA", ga.pop[i, :])# something about plottingif 'sca' in globals(): sca.remove()sca = plt.scatter(DNA_prod, pred, s=200, lw=0, c='red', alpha=0.5);plt.pause(0.05)plt.ioff()plt.show()