RSA加密与解密原理

一、什么是RSA加密

二、RSA加密原理

三、RSA加解密过程与算法代码

一、什么是RSA加密

RSA加密是一种非对称加密算法。

对称加密：

对称加密是一种加密方式，加密和解密使用同一个密钥，被加密的信息在传输前用预先协商好的密钥进行加密，接收方再用同样的密钥进行解密。这种方式的优点是加密效率高、加解密速度快，但是缺点是密钥需要事先共享，如果密钥被泄漏，则加密无效。

常见的对称加密算法包括DES、3DES、AES等。

非对称加密：

非对称加密是一种加密方式，加密和解密使用不同的密钥。发送方使用公钥进行加密，接收方使用私钥进行解密。因为公钥可以公开，所以只有私钥知道的加密信息能够被解密，这种方式的优点是安全性高，缺点是相对于对称加密而言，加密速度较慢。

二、RSA加密原理

涉及到的数学术语

质数（prime number）是指大于1且只能被1和自身整除的正整数，例如2、3、5、7等。
公共模数（common modulus）是指在加密算法中使用相同的模数进行加密或解密操作。多个用户可以使用相同的模数进行加密，但需要不同的密钥进行解密。
欧拉函数（Euler's totient function），也称为φ函数，描述了小于某个正整数n且与n互质的正整数的个数。具体计算方法根据n的素因数分解进行推导，例如对于质数p，φ(p) = p - 1，对于两个互质的质数p和q，φ(pq) = (p - 1)(q - 1)。
互质数（coprime numbers）指的是两个或多个整数的最大公因数为1的非零自然数。换句话说，互质数之间没有共同的因数，除了1以外没有其他公共因数。例如，2和3是互质数，因为它们的最大公因数是1；而6和9不是互质数，因为它们的最大公因数是3。

三、RSA加解密过程与算法代码

1.随机选取1对质数

选取的质数的值越大越安全。

2.计算公共模数

n = p * q

如果质数越大，则乘积n越大。乘积n越大。n转换为二进制后对应的加密位数越长。越长的加密位数，越容易引发雪崩效应，以减小数据的关联性。故越安全。

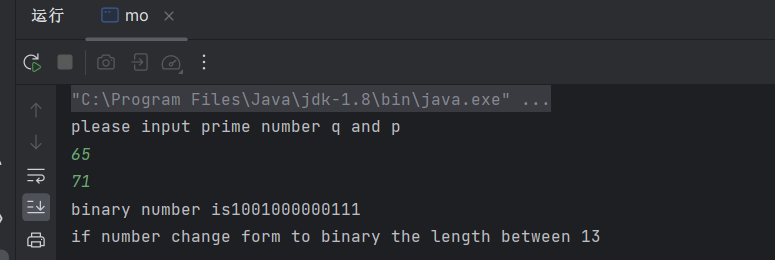
假设p = 65 q = 71 ,则n = 4615,对应的二进制为1001000000111,长度为13位。

算法（Java）：

public class mo {public static void main(String[] args) {int q,p;int number;Scanner scanner = new Scanner(System.in);System.out.println("please input prime number q and p");q= scanner.nextInt();p = scanner.nextInt();number = q*p;String str;
//        change number's form into binarystr = Integer.toBinaryString(number);System.out.println("binary number is"+str);System.out.println("if number change form to binary the length between "+ str.length());}
}

3.计算欧拉函数

φ(n) = φ(p*q) = (p-1)(q-1)

φ函数计算的是1~n之中的互斥数的个数。

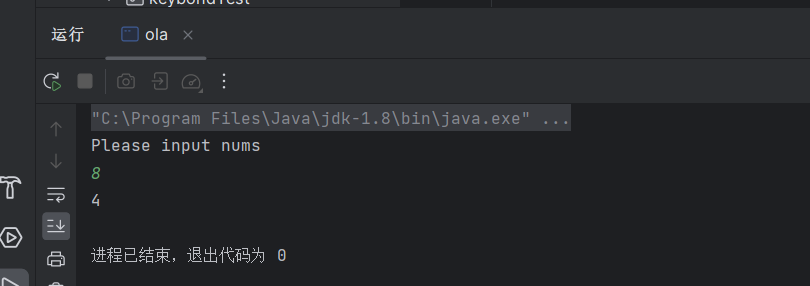
当n=8时候，互质数为1,3,5,7 即φ(8) = 4

互斥数的个数计算算法代码（Java）

public class ola {public static void main(String[] args) {
//        setting count to caculate the number of coprime numbersint count = 0;System.out.println("Please input nums");Scanner scanner = new Scanner(System.in);//        caculateif (scanner.hasNext()){int num = scanner.nextInt();for (int i = 0 ;i<num;i++){
//                analyse "i" is coprime numbersif (BigInteger.valueOf(i).gcd(BigInteger.valueOf(num)).intValue() == 1){count++;}}}System.out.println(count);}
}

4.生成公钥

1 < e < φ(n)

注意：

e 的取值必须是整数
e 和 φ(n) 必须是互质数

公钥e的取值算法（Java）：

public class publicKey {public static void main(String[] args) {int num;Scanner scanner = new Scanner(System.in);System.out.println("Please input number");num = scanner.nextInt();//        public Key is coprime number to num between 1 to numSystem.out.println("e's value can be ");for (int i = 0;i<num;i++){if (BigInteger.valueOf(i).gcd(BigInteger.valueOf(num)).intValue() ==1){System.out.printf(i+"、");}}}
}

5.生成私钥

e * d % m = 1 其中(φ(n) = m)

其中d就是所谓的私钥，而求取d的方式就是解出二元一次方程式.

解除这个二元一次方程式可以通过扩展欧几里得算法进行求解

扩展欧几里得算法：

扩展欧几里得算法（Extended Euclidean Algorithm）是一种用于求解两个整数的最大公约数（Greatest Common Divisor，简称GCD），以及它们的线性组合的算法。该算法还可以用于解决一元线性同余方程。

假设有两个非零整数a和b，我们的目标是找到它们的最大公约数d，以及两个整数x和y，使得满足贝祖等式：ax + by = d。

扩展欧几里得算法的步骤如下：

首先，我们用辗转相除法求出a除以b的余数r，并更新a为原来的b，b为原来的r，重复这一步骤直到余数r为0。
一旦余数r为0，我们找到了d，即a和b的最大公约数。
接下来，我们倒回去进行递归计算。初始时，我们有两个系数x和y为1，然后通过迭代，更新它们的值，直到达到基本情况（b=0）。在每一步迭代中，我们用之前的系数减去当前商乘以之前的系数，以便保持贝祖等式成立。
当递归结束时，得到的两个系数x和y就是满足贝祖等式的整数解。

扩展欧几里得算法在密码学、模运算等领域有广泛的应用，例如求取模反元素、计算模逆等。它的时间复杂度为O(log min(a,b))，效率较高。

算法（Java）：

public static int[] extendGcd(int a, int b) {int[] result = new int[3];if (b == 0) {result[0] = a;result[1] = 1;result[2] = 0;return result;}int[] temp = extendGcd(b, a % b);result[0] = temp[0];result[1] = temp[2];result[2] = temp[1] - (a / b) * temp[2];return result;
}

6.公钥加密

public class encryption {public static void main(String[] args) {
//        明文 与密文int M;double C;//        公钥 与公共模数int e;int num;Scanner scanner = new Scanner(System.in);System.out.println("Plase input 明文、公钥、公共模数");M = scanner.nextInt();e = scanner.nextInt();num = scanner.nextInt();//        加密算法C = Math.pow(M,e) % num;System.out.println("密文为："+C);}
}

7.私钥解密