**时间序列分析(time series analysis)是量化投资中的一门基本技术。时间序列是指在一定时间内按时间顺序测量的某个变量的取值序列。**比如变量是股票价格,那么它随时间的变化就是一个时间序列;同样的,如果变量是股票的收益率,则它随时间的变化也是一个时间序列。时间序列分析就是使用统计的手段对这个序列的过去进行分析,以此对该变量的变化特性建模、并对未来进行预测。
时间序列分析试图通过研究过去来预测未来。
一个时间序列可能存在的特征包括以下几种:
-
**趋势:**趋势是时间序列在某一方向上持续运动(比如牛市时股市每天都在上涨,股票收益率持续为正;熊市时股市每天都在下跌,股票收益率持续为负)。趋势经常出现在金融时间序列中,特别是大宗商品价格;许多商品交易顾问(CTA)基金在他们的交易算法中都使用了复杂的趋势识别模型。
-
**季节变化:**许多时间序列中包含季节变化。在金融领域,我们经常看到商品价格的季节性变化,特别是那些与生长季节或温度变化有关的商品,比如天然气。
-
**序列相关性:金融时间序列的一个最重要特征是序列相关性(serial correlation),又称为自相关性(autocorrelation)。**以投资品的收益率序列为例,我们会经常观察到一段时间内的收益率之间存在正相关或者负相关。此外,波动聚类(volatility clustering)也是一种序列相关性,它意味着高波动的阶段往往伴随着高波动的阶段出现、低波动的阶段往往伴随着低波动的阶段出现,这在量化投资中尤为重要。比如下图为 2001 年到 2017 年上证指数日收益率的标准差,从中可以清晰的看到波动聚类。
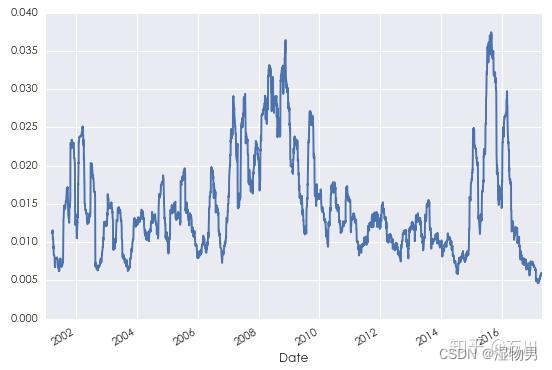
**随机噪声:**它是时间序列中除去趋势、季节变化和自相关性之后的剩余随机扰动。由于时间序列存在不确定性,随机噪声总是夹杂在时间序列中,致使时间序列表现出某种震荡式的无规律运动。
量化投资的交易者的目标是利用统计建模来识别金融时间序列中潜在的趋势、季节变化和序列相关性。
金融时间序列的关系中,最重要的当属**自相关性。**对于金融时间序列,比如投资品的收益率,看似随机的时间序列中往往存在着惊人的自相关。对自相关建模并加以利用能够大幅提高交易信号的准确性。配对交易的均值回复策略就是这么一个例子。均值回复策略利用一对投资品价差序列的负相关性进行投资,产生做多或者做空的交易信号,实现盈利。
金融时间序列分析的核心就是挖掘该时间序列中的自相关性。
协方差和相关系数
协方差是有量纲的,因此它的大小受随机变量本身波动范围的影响
当两个随机变量的波动范围扩大 100 倍后,它们的协方差扩大了 10000 倍。因此,人们希望使用某个和协方差有关,但是又是无量纲的测量来描述两个随机变量的相关性。最简单的做法就是用变量自身的波动对协方差进行标准化。相关系数(correlation 或者 correlation coefficient)便由此得来。
令 ρ \rho ρ表示 x和 y 的总体相关系数(population correlation),它的定义为:
ρ ( X , Y ) = E [ ( X − μ X ) ( Y − μ Y ) ] σ X σ Y = C o v ( X , Y ) σ X σ Y \rho(X,Y)=\frac{E[(X-\mu_{X})(Y-\mu_{Y})]}{\sigma_X\sigma_Y}=\frac{Cov(X,Y)}{\sigma_X\sigma_Y} ρ(X,Y)=σXσYE[(X−μX)(Y−μY)]=σXσYCov(X,Y)
其中 σ X \sigma_X σX和 σ Y \sigma_Y σY 分别为 X和 Y 的总体标准差(population standard deviation)。通过使用 X 和Y 的标准差对它们的协方差归一化, ρ \rho ρ 的取值范围在 -1 到 +1 之间,即 [-1, +1]:

时间序列的平稳性
平稳性(stationarity)是时间序列分析的基础。

自相关性和自相关系数
假设我们有弱平稳的投资品收益率序列 { r t } \{ r_t \} {rt} 。自相关性考察的是 t时刻的收益率 r t r_t rt和距当前任意间隔 k时刻的收益率 r t − k r_{t-k} rt−k 之间的线性相依关系( k 的取值是所有 $\geq$0的整数)。由于 r t r_t rt 和 r t − k r_{t-k} rt−k 来自同一个时间序列,因此我们将第三节中的相关系数的概念应用到 r t r_t rt 和 r t − k r_{t-k} rt−k 上,便推广出自相关系数(autocorrelation)。
相关图在我们对时间序列建模时至关重要。
拿来一个收益率序列,只要画出相关图,就可以检测该序列在任何间隔 有无统计上显著的自相关性。
对金融时间序列建模,最重要的就是挖掘出该序列中的不同间隔 的自相关性。相关图可以帮助我们判断模型是否合适 如果模型很好的捕捉了自相关性,那么原始时间序列与模型拟合的时间序列之间的残差应该近似的等于随机噪声。
对于任意不为 0 的间隔,随机噪声的自相关均为 0。
显然,间隔为 0 的自相关系数为 1;
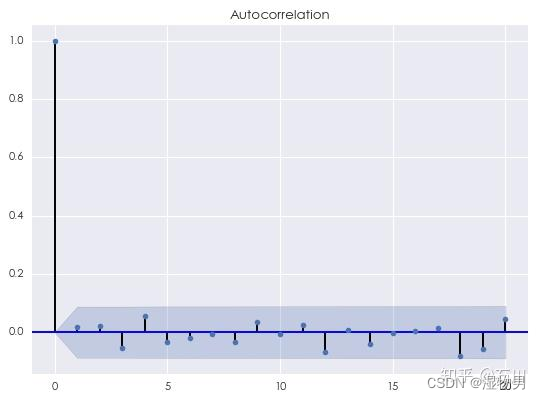

因此,在评价对金融时间序列的建模是否合适时,我们首先找到原始时间序列和它的拟合序列之间的残差序列;然后只要画出这个残差序列的相关图就可以看到它是否含有任何模型未考虑的额外自相关性:
如果残差的相关图和上面这个图相似,则可以认为残差是一个随机噪声,而模型已经很好的捕捉了原始时间序列中的自相关性;
如果残差的相关图体现了额外的自相关性,它们将为我们改进已有的模型提供依据,因为这些额外的自相关说明已有模型没有考虑原始时间序列在某些特定间隔上的自相关。





——基本指令)









之UBSAN动态代码分析)



硬件加速卡)